树、二叉树、查找算法总结
树、二叉树、查找算法总结
一:思维导图
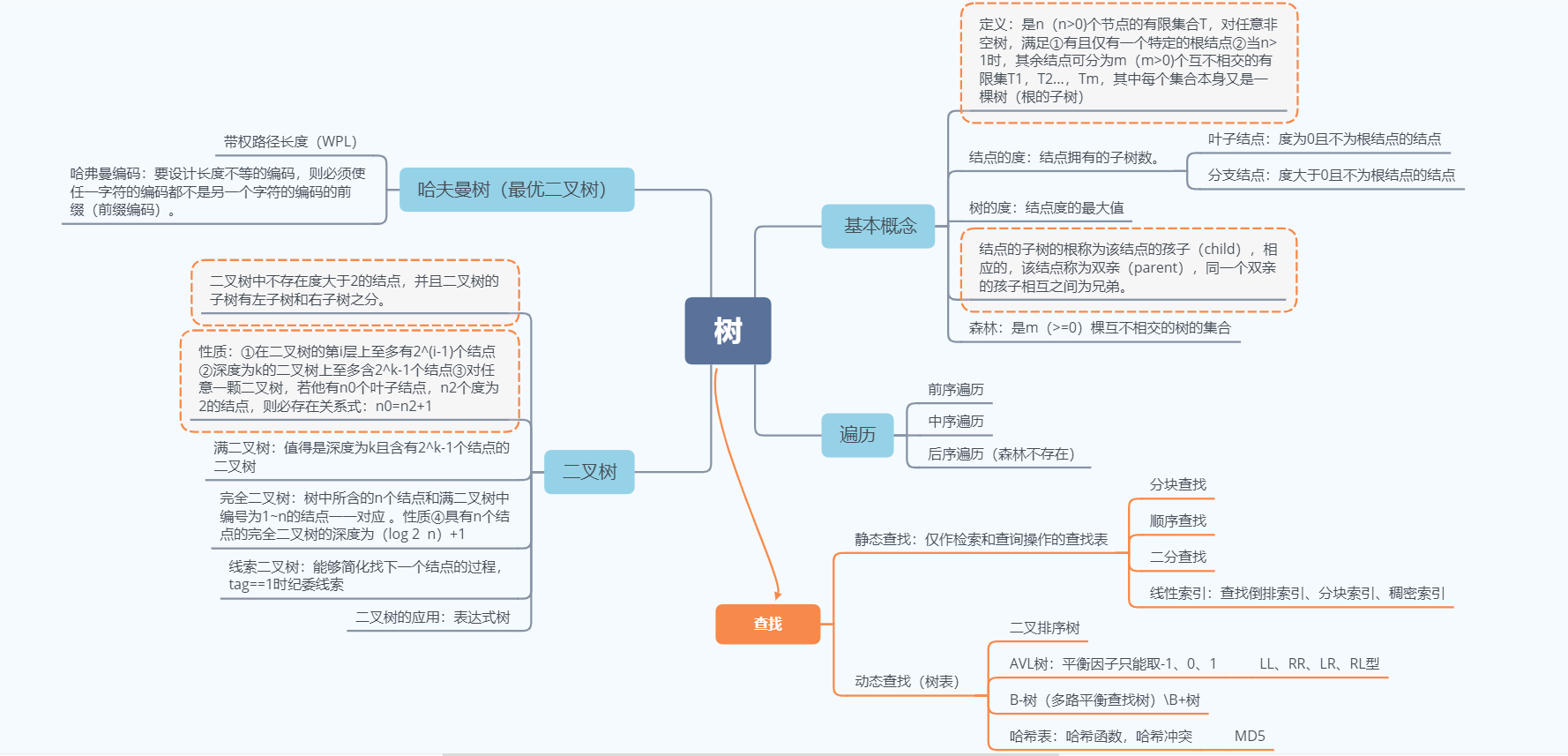
二:重要概念笔记
-
树
-
定义:是n(>=0)个结点的有限集合T,对于任意一棵非空树,满足:①有且仅有一个特定的根结点②当n>1时,其余结点可分为m(m>0)个互不相交的有限集T1、T2、...、Tm,其中每个集合本身又是一棵树,称为根的子树。
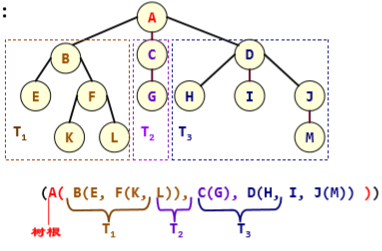
-
结点的度:结点拥有的子树数。叶子(或终端)结点:度为零的结点。分支(或非终端)结点:度大于零的结点。
-
树的度:树中所有结点的度的最大值。结点的子树的根称为该结点的孩子结点 。相应的,该结点称为孩子的双亲结点。同一个双亲的孩子之间互称兄弟。
-
森林:是m(m≥0)棵互不相交的树的集合。
-
树的存储结构:
双亲表示法:快速找到双亲结点
typedef struct PTNode { Elemtype data; int parent; } PTNode;孩子链表表示法:快速查找到每个结点的孩子结点
typedef struct CTNode { int child; struct CTNode *next; } *ChildPtr; typedef struct { Elemtype data; ChildPtr firstchild; } CTBox;孩子-兄弟表示法:左孩子右兄弟
typedef struct CSNode{ Elemtype data; struct CSNode *firstchild, *nextsibling; } CSNode, *CSTree; -
树的遍历和二叉树遍历的对应关系:
树: 先根遍历 后根遍历
森林: 先序遍历 中序遍历
二叉树:先序遍历 中序遍历
ps:树的后根遍历与对应二叉树的中根遍历顺序是一致的
-
-
二叉树
-
定义:是n(n>=0)个结点的有限集合,它或为空 树(n=0),或由一个根结点和至多两棵称为根的 左子树和右子树的互不相交的二叉树组成。 注:二叉树中不存在度大于2的结点,并且二叉树 的子树有左子树和右子树之分。
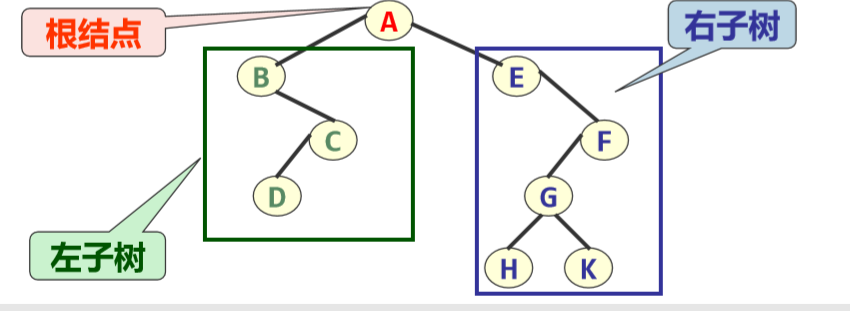
-
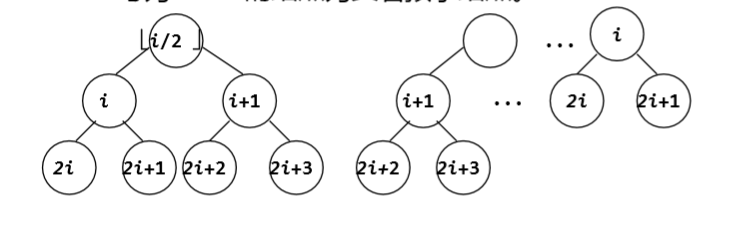
性质:① 在二叉树的第 i 层上至多有2i-1 个结 点(i≥1)。②深度为 k 的二叉树上至多含 2k-1 个结 点(k≥1)。 ③对任何一棵二叉树,若它含有n0 个叶子 结点、n2 个度为2的结点,则必存在关系式:n0 = n2+1。 ④(完全二叉树的性质):具有n个结点的完全二叉树的深度为 (log2n)+1。 ⑤(完全二叉树的性质):若对含 n 个结点的完全二叉树从上到下且 从左至右进行 1 至 n 的编号,则对完全二叉树中 任意一个编号为 i 的结点: (1)若 i=1,则该结点是二叉树的根,无双亲,否 则,编号为i/2的结点为其双亲结点;
(2)若 2i>n,则该结点无左孩子,否则,编号为 2i 的结点为其左孩子结点;
(3)若 2i+1>n,则该结点无右孩子结点,否则,编 号为2i+1 的结点为其右孩子结点。
-
特殊二叉树:
满二叉树:指的是深度为k且含有2k-1个结点的二 叉树。
完全二叉树:树中所含的 n 个结点和满二叉树中 编号为 1 至 n 的结点一一对应。
-
存储结构:
顺序存储:一组地址连续的存储单元存储各结点(如一维数组) ;自根而下、自左而右存储结点;按完全二叉树上的结点位置进行编号和存储。缺点:空间利用率低。
链式存储:二叉链表
typedef struct BiTNode { TElemType data; struct BiTNode *lchild, *rchild; } BiTNode, *BiTree;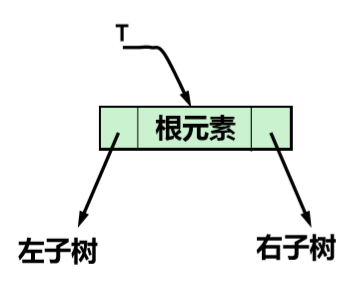
三叉链表:
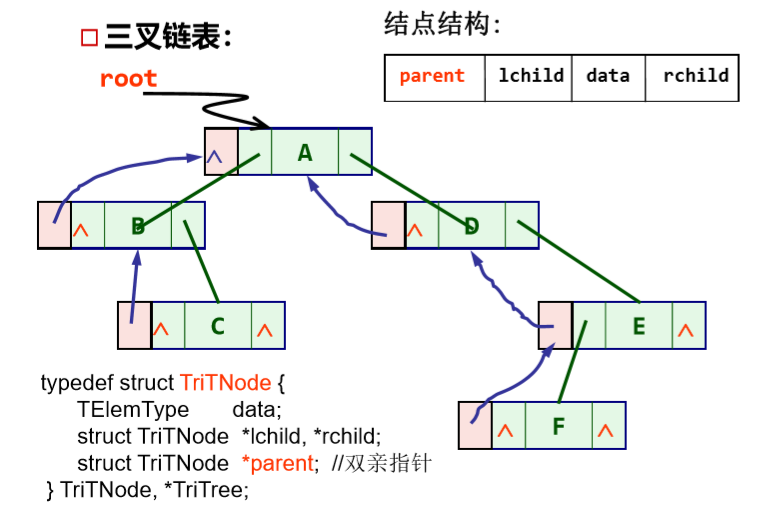
-
遍历二叉树:
先序遍历:
void Preorder (BiTree T) { if (T) { cout<<T->data; //先访问结点 Preorder(T->lchild); Preorder(T->rchild); } }中序遍历:
void Inorder (BiTree T) { if (T) { Inorder(T->lchild); cout<<T->data; Inorder(T->rchild); } }后序遍历:
void Inorder (BiTree T) { if (T) { Inorder(T->lchild); Inorder(T->rchild); cout<<T->data; } } -
线索二叉树:指向该线性序列中的“前驱”和 “后继” 的指针, 称作“线索”。线索二叉树能简化找到下一个节点的这个过程。
typedef struct BiThrNod { TElemType data; struct BiThrNode *lchild, *rchild; int LTag, RTag; /*当Tag=1,说明该处无孩子结点,为线索*/ } BiThrNode, *BiThrTree;
-
-
二叉排序(查找)树
- 二叉排序树:或者是一棵空树;或者是具有如下特性的二叉树:若它的左子树不空,则左子树上所有结点的值均小于根结点的值;若它的右子树不空,则右子树上所有结点的值均大于根结点的值。它的左、右子树也都分别是二叉排序树。
- 特点:中序遍历得到一个关键字递增的有序序列
- 二叉排序树实现:
-
哈夫曼树
-
结点的路径长度:从根结点到该结点的路径上分支的数目。
树的路径长度:树中每个结点的路径长度之和。
树的带权路径长度(WPL):树中所有叶子结点的带权路径长度之和。
-
构造:选取其根结点的权值最小的两棵二叉树,分别作为左、右子树构造一棵新的二叉树,并置这棵新的二叉树根结点的权值为其左、右子树根结点的权值之和。
-
哈夫曼编码:关键要设计长度不等的编码,则必须使任一字符的编码都不是另一个字符的编码的前缀,出现频率越大的字符,其哈夫曼编码越短。
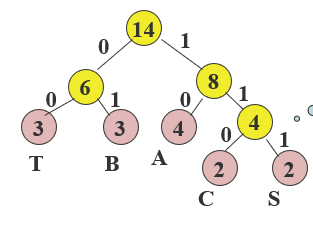
-
-
平衡二叉树
-
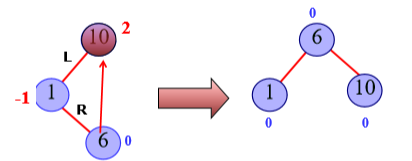
LL/RR平衡旋转
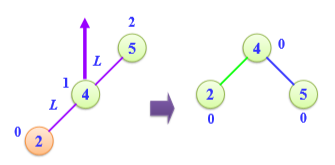
-
LR/RL平衡旋转
-
-
B-树和B+树
-
:一个节点可放多个关键字,降低树 的高度。数据可放外存,适合大数据量查找。节 点数据从外存中读取,一次读取多个,效率高。
-
B-树特点:非根结点孩子结点个数至少为m/2,至多m;关键字个数至少m/2-1,至多m-1;根结点至少两个孩子结点
typedef struct BTNode { int keynum; struct BTNode *parent; KeyType key[m]; struct BTNode *ptr[m]; Record *recptr[m]; } BTNode, *BTree;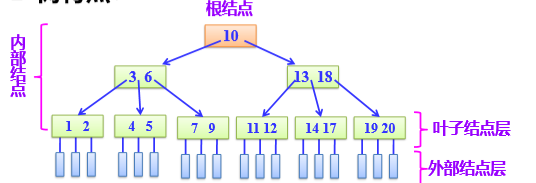
- B-插入:在查找不成功之后,需进行插入。关键字插入的位 置必定在叶子结点层,有下列几种情况:插入后,该结点的关键字个数n<m-1,不修改指针; 插入后,该结点的关键字个数 n=m-1,则需进行 “结点分裂”。分裂过程,如果没有双亲结点,新建一个双亲结点,数的高度增加一层;如果有双亲结点,将k插入双亲结点中。
-
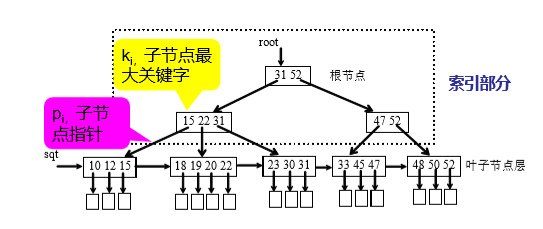
B+树:B+树中所有非叶子节点仅起到索引的作用。通常在B+树上有两个头指针,一个指向根节点, 另一个指向关键字最小的叶子节点,所有叶子节 点链接成一个不定长的线性链表。
-
-
顺序查找
-
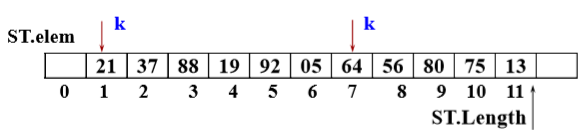
以顺序表或线性链表表示静态查找表
-
int LocateELem(SqList L,ElemType e) { for (k = 1; k <= L.length; k++) { if (L.elem[k] == e) return k; } return 0; } -
平均查找长度ASL=n+1/2
-
-
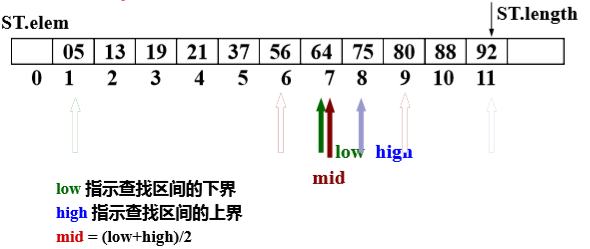
折半查找
-
-
int Search_Bin ( SSTable ST, KeyType key ) { low = 1; high = ST.length; while (low <= high) { mid = (low + high) / 2; if (EQ (key , ST.elem[mid].key) ) return mid; else if ( LT (key,ST.elem[mid].key) ) high = mid - 1; //在前半区间查找 else low = mid + 1; //在后半段区间进行查找 } return 0; } -
平均查找长度ASL≈log2(n+1)-1
-
-
线性索引查找
-
分块索引
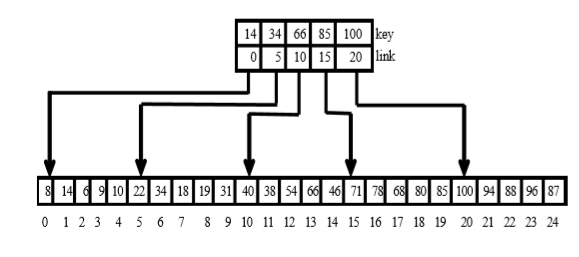
-
倒排索引:广泛适用于搜索引擎
-
稠密索引
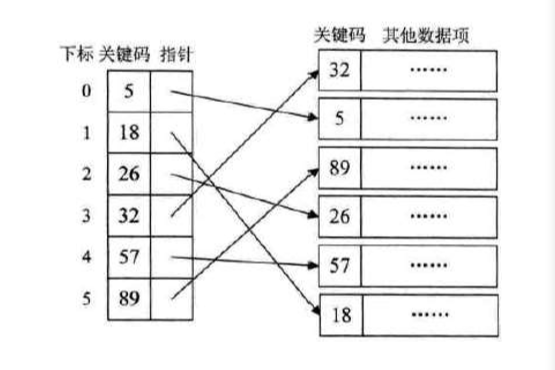
-
-
哈希表
-
哈希函数H(key):映像,一般情况下,容易产生哈希冲突。关键字选取构造方法一般有:直接定址法(H(key) =key或者H(key)=a × key+b)、数字分析法、平方取中法、折叠法(移位叠加和间界叠加)、除留余数法(最常用H(key)=key MOD p,p应为不大于m 的素数)、随机数法(H(key)=Random(key))。
-
处理冲突:
-
开放定址
线性探测再散列 di = c × i 最简单的情况c= 1
二次探测再散列 di = 12, -12, 22, -22 , …, ± k 2 , ( k ≤ m / 2)随机探测再散列 di 是一组伪随机数列 或者 di =i × H 2 (key) (又称双散列函数探测)
ASL计算eg:
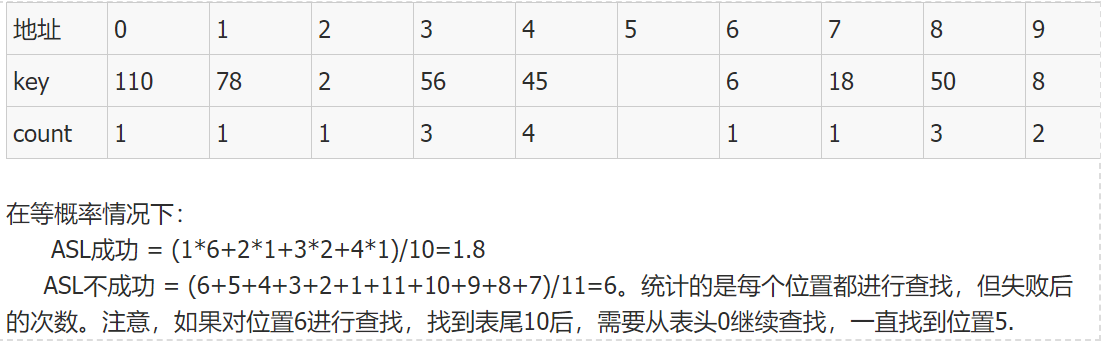
-
再哈希法
-
链地址法
将所有哈希地址相同的记录都链接在统一链表中。
ASL计算eg:

-
建立公共溢出区
-
-
MD5:一种算法,可以将一个字符串,或 文件,或压缩包,执行md5后,就可以生成一个固 定长度为128bit的串。
-
三:疑难问题及解决方案
-
设一组初始记录关键字集合为(25,10,8,27,32,68),散列表的长度为8,散列函数H(k)=k mod 7,要求:1.分别用线性探测法和链地址法作为解决冲突的方法设计哈希表。2.计算线性探测法和链地址法成功和不成功的ASL。
我的答案:
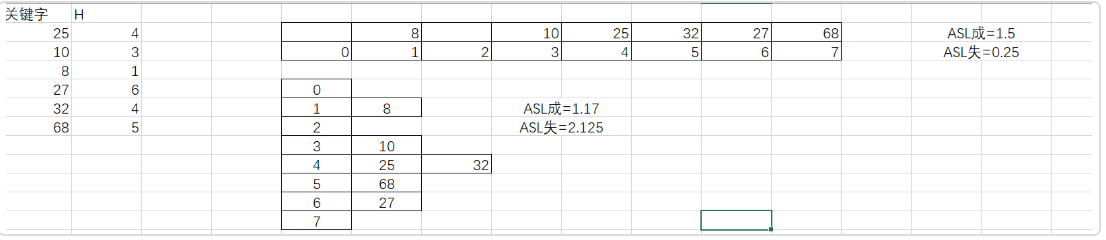
正确答案:

解决方法:
重新细看了超星的视频以及老师的课件,问同学,最后知道ASL失败的正确算法。因为一开始我把他和二叉排序树的ASL计算混合在一起了。

