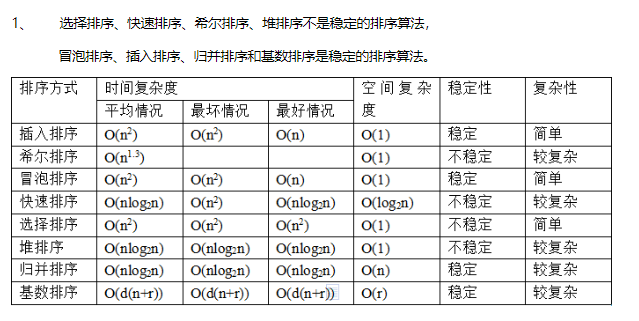
Java常用数据结构算法——排序
-
二分查找算法(折半)
-
原理
1.待查找的序列有序
2.每次查找都取中间位置的值与待查关键字key比较，若干中间位置的值比key大，则在序列左半部分继续执行该查找；若相等 则返回mid；若比key小，则在序列的右半部分执行该查找过程，指导查到关键字为止。
-
coding
public class binarySearch { public static int binarySearch_fun(int [] arr,int key){ /** * @Author: hcx * @Description: 二分查找算法 * @Date: 2022/6/13 20:32 * @Param: [arr, key] 有序数据 待查值 * @return: int **/ int mid,low,high; low = 0; high = arr.length-1; mid = (high-low)/2+low; while (low<high){ if(arr[mid]>key){//中间值比检索值大，则向左边检索 low不变 high = mid-1; mid = (high-low)/2+low; } else if (arr[mid]== key) { return arr[mid] mid; }else {//中间值比检索值小，则向右边检索 high不变 low=mid+1; mid = (high-low)/2+low; } } return -1; } public static void main(String[] args) { // int [] arr={3,4,6,20,40,45,51,62,70,99,110}; int res=binarySearch_fun(arr,20); System.out.println(res); } } -
时间复杂度
O(logn)
-
-
冒泡排序
-
原理
1.比较相邻的元素。如果前一个元素比后一个元素大，就交换这两个元素的位置
2.对每一组相邻的元素做同样的工作，从开始第一队到结尾最后一对。最终最后位置的元素就是max。
-
coding
import java.util.Arrays; public class bubbleSort { public static int[] bubbleSort_fun(int[] arr){ /** * @Author: hcx * @Description: 冒泡排序，从左到右比较 每轮提取最大的值到尾部 时间复杂度O（n²）双层循环； * @Date: 2022/6/13 21:46 * @Param: [arr] * @return: int[] **/ for(int i=0;i<arr.length-1;i++){ for(int j = 0 ;j<arr.length-1-i;j++){ if(arr[j] > arr[j+1]){//交换位置 int tmp = arr[j+1]; arr[j+1] = arr[j]; arr[j] = tmp; } } } return arr; } public static void main(String[] args) { // int [] arr={4,5,6,3,2,1}; int [] res=bubbleSort_fun(arr); System.out.println(Arrays.toString(res)); } } -
时间复杂度
O(n^2)
-
-
插入排序算法
-
原理
将一个数据插入到已经排好序的序列中。
-
coding
import java.util.Arrays; public class insertionSort { public static int[] insertionSort_fun(int[] arr){ /** * @Author: hcx * @Description: 插入排序，在完全有序的情况下，插入排序每个未排序区间元素只需要比较1次，所以时间复杂度是O(n)。而在极端情况完全逆序，时间复杂度为O(n^2).就等于每次都把未排序元素插入到数组第一位。 * @Date: 2022/6/13 22:51 * @Param: [arr] * @return: int[] **/ for(int i=1;i<arr.length;i++){ int insertVal = arr[i];//插入的值 int index=i-1;//被插入的位置 准备和前一个位置比较 //插入的数比被插入的数小 while(index>=0&&insertVal<arr[index]){ //交换位置 arr[index+1]=arr[index];//将arr[index]向后移动 index--;//将index索引向前移动 } arr[index+1]=insertVal;//将被插入的数放入合适的位置 } return arr; } public static void main(String[] args) { // int [] arr={4,5,6,3,2,1}; int [] res=insertionSort_fun(arr); System.out.println(Arrays.toString(res)); } } -
时间复杂度
最坏情况：O(n^2) 最好情况O(n) 平均情况O(n^2)
-
-
快速排序算法
-
原理
-
冒泡的改进
-
选择基准值（一般默认设置第一个值为基准值）
-
设置头尾为low、high
-
从后向前比较，如果比基准值，则交换位置；
-
从前向后比较，若比基准值大就交换位置6. 重复迭代上述过程，直到整个序列有序
-
-
coding
import java.util.Arrays; public class quickSort { public static int [] quicksort_fun(int [] arr,int low,int high){ /** * @Author: hcx * @Description: 快拍-递归处理 * @Date: 2022/6/15 15:43 * @Param: [arr, low, high] * @return: int[] **/ int start =low; int end = high; int key = arr[low];//基准值 //从后向前与基准值比较 while (end > start){ while (end>start&&arr[end]>=key){//从后向前比较 ,知道出现小于基准值的 end--; } //出现小于基准值的 交换位置 if(arr[end]<=key){ arr[start] = arr[end]; arr[end] = key; } //从前向后比较 while (end>start&&arr[start]<=key){//从前向后比较 ,知道出现大于基准值的 start++; } if(arr[start]>=key){ arr[end]=arr[start]; arr[start]=key; } //此时第一次循环结束 基准值的位置确定 左边的都比基准值小 } //递归处理左边序列 if(start>low) quicksort_fun(arr,low,start-1); //递归处理右边序列 if(end<high) quicksort_fun(arr,end+1,high); return arr; } public static void main(String[] args) { // int[] arr={6,9,5,7,8}; int[] res=quicksort_fun(arr,0,arr.length-1); System.out.println(Arrays.toString(res)); } } -
时间复杂度
平均时间复杂度和最优时间复杂度都是O(nlogn),而最差时间复杂度O(n^2)。
-
-
希尔排序算法
-
原理
shell sort是插入排序算法的一种，又叫做【缩小增量排序】——属于非稳定排序算法
希尔排序算法将数据按下标的一定增量进行分组，对每组使用插入排序算法进行排序，随着增量逐渐减少，每组包含的关键词越来越多，在增量减至1时，整个文件被分为一组，算法终止！
increment= increment/2
increment= increment/2
....
len= 1 -
coding
public class ShellSort { //核心代码---开始 public static void sort(Comparable[] arr) { int j; for (int gap = arr.length / 2; gap > 0; gap /= 2) {//分组 每次组大小除2 直到组为1 for (int i = gap; i < arr.length; i++) { Comparable tmp = arr[i]; for (j = i; j >= gap && tmp.compareTo(arr[j - gap]) < 0; j -= gap) { arr[j] = arr[j - gap]; } arr[j] = tmp; } } } //核心代码---结束 public static void main(String[] args) { int N = 2000; Integer[] arr = {4,5,6,3,2,1,7}; ShellSort.sort(arr); for( int i = 0 ; i < arr.length ; i ++ ){ System.out.print(arr[i]); System.out.print(' '); } } } -
时间复杂度
O(n^(1.3-2))
-
-
归并排序算法
-
原理
归并排序是建立在归并操作上的一种有效，稳定的排序算法，该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。
-
coding
import java.util.Arrays; public class mergeSort { public static void main(String[] args) { // int[] arr={6,9,5,7,8,1,3}; int[] res=mergeSort_fun(arr); System.out.println(Arrays.toString(res)); } public static int[] mergeSort_fun(int [] data){ /** * @Author: hcx * @Description: 归并排序——分治法 * @Date: 2022/6/15 17:06 * @Param: [data] * @return: int[] **/ sort(data,0,data.length-1); return data; } public static void sort(int [] data,int left, int right){ if(left>=right){ return; } //中间索引 int center=(right+left)/2; //对左边数组进行排序 sort(data,left,center); //对右边数组进行排序 sort(data,center+1,right); //将两个数组进行合并 merge(data,left,right,center); } public static void merge(int [] data,int left,int right,int center){ int [] tmpArr=new int [data.length];//临时数组 int middle=center+1;//右边第一个元素索引 int third=left;//临时数组索引 int tmp=left;//左边第一个元素索引 while (left<=center&&middle<=right){//将排好的子序列合并 if(data[left]<=data[middle]){ tmpArr[third++]=data[left++]; }else { tmpArr[third++]=data[middle++]; } } //将剩余部分依次存放入临时数组中 while (middle<=right){ tmpArr[third++]=data[middle++]; } while ((left<=center)){ tmpArr[third++]=data[left++]; } //将临时数组复制到原数组中 while (tmp<=right){ data[tmp]=tmpArr[tmp++]; } } } -
时间复杂度
O(nlogn)
-
-
桶排序算法
-
原理
原理是先找出待排序列中的最大值和最小值，并根据最大值和最小值定义桶，然后将数据按照大小放入桶中，最后对每个桶进行排序。
例如
待排序列：3 6 5 9 7 8
max：9 min：3
设置0-3、4-7、8-10为桶
0-3:3
4-7:6 5 7
8-10：9 8 -
coding
package hcx.main.offer.chapter5DS; import java.util.ArrayList; import java.util.Arrays; import java.util.Collections; public class bucketSort { public static int [] bucketSort_fun(int [] arr){ /** * @Author: hcx * @Description: 桶排序 * @Date: 2022/6/15 17:25 * @Param: [arr] * @return: int[] **/ int max=Integer.MIN_VALUE;//最大值 int min=Integer.MAX_VALUE;//最小值 for (int i=0;i<arr.length;i++){//取得最大值和最小值 max=Math.max(max,arr[i]); min=Math.min(min,arr[i]); } //创建通 int bucketNum=(max-min)/arr.length+1;//桶的数量 ArrayList<ArrayList<Integer>> bucketArr=new ArrayList<>(bucketNum);//初始化桶数组 for(int i=0;i<bucketNum;i++){ bucketArr.add(new ArrayList<Integer>()); } for (int i=0;i<arr.length;i++){//将每个元素放入桶中 int num=(arr[i]-min)/arr.length;//判断该元素在那个桶中 bucketArr.get(num).add(arr[i]); } //对每个桶进行排序 for(int i=0;i<bucketArr.size();i++){ Collections.sort(bucketArr.get(i)); } ArrayList<Integer> result=new ArrayList<>();//结果 for (int i=0;i<bucketArr.size();i++){//将排序后的痛进行合并 result.addAll(bucketArr.get(i)); } for (int i=0;i<result.size();i++){//将list赋予到arr数组 arr[i]=result.get(i); } return arr; } public static void main(String[] args) { // int[] arr={6,9,5,7,8,1,3}; int[] res=bucketSort_fun(arr); System.out.println(Arrays.toString(res)); } } -
时间复杂度
桶排序算法遍历了2次原始数组，运算量为2N，最后，遍历桶输出排序结果的运算量为N，初始化桶的运算量为M。
对桶进行排序，不同的排序算法算法复杂度不同，冒泡排序算法复杂度为O(N^2)，堆排序、归并排序算法复杂度为O(NlogN)，我们以排序算法复杂度为O(NlogN)进行计算，运算量为N/Mlog(N/M)M
最终的运算量为3N+M+N/Mlog(N/M)M，即3N+M+N(logN-logM)，去掉系数，时间复杂度为O(N+M+N(logN-logM))
-
-
基数排序算法
-
原理
将所有待比较数据统一为同一长度，在位数不够是前面补零，然后从低位到高位根据每个位上整数的大小排序，最终得到一个有序序列。
-
coding
import java.util.Arrays; public class radixSort { public static int [] radixSort_fun(int[] arr,int maxDigit){ /** * @Author: hcx * @Description: 基数排序 * @Date: 2022/6/15 17:53 * @Param: [arr, maxDigit]待排序数组、数组中的最大位数 * @return: int[] **/ double max=Math.pow(10,maxDigit+1); // System.out.println(max); int n=1;//代表位数对应的数值 1 10 100 ......... int k=0;//保存每一位排序后的结果用于下一位的排序输入 int len=arr.length; int[][] bucket=new int[10][len];//保存每次排序后的结果 int[] order=new int[10];//保存每个通里有多少个数字 while (n<max){ for(int num:arr){ int digit=(num/n)%10;//提取位数上的数字 bucket[digit][order[digit]]=num; order[digit]++; } //将当前循环生成的桶里的数据覆盖到原来数组中，用于保存这一位的排序结果; for(int i=0;i<len;i++){ if(order[i]!=0){ for(int j=0;j<order[i];j++){ arr[k]=bucket[i][j]; k++; } } order[i]=0;//排完后释放 } n*=10; k=0;//释放，用于下一位的排序 } return arr; } public static void main(String[] args) { // int[] arr={61,119,25,17,8,1,3}; int[] res=radixSort_fun(arr,3); System.out.println(Arrays.toString(res)); } } -
时间复杂度
为O (nlog(r)m)，其中r为所采取的基数，而m为堆数，在某些时候，基数排序法的效率高于其它的稳定性排序法。
-
-
其他算法
- 剪枝：算法优化，by剪枝策略，减少不必要的路径。
- 回溯：最优选择搜索算法
- 最短路径算法:Dijkstra、Floyd
-
补充
脚踏实地，注重基础。
