Loj #2570. 「ZJOI2017」线段树
Loj #2570. 「ZJOI2017」线段树
题目描述
线段树是九条可怜很喜欢的一个数据结构,它拥有着简单的结构、优秀的复杂度与强大的功能,因此可怜曾经花了很长时间研究线段树的一些性质。
最近可怜又开始研究起线段树来了,有所不同的是,她把目光放在了更广义的线段树上:在正常的线段树中,对于区间 \([l, r]\),我们会取 \(m = \lfloor \frac{l+r}{2} \rfloor\),然后将这个区间分成 \([l, m]\) 和 \([m + 1, r]\) 两个子区间。在广义的线段树中,\(m\) 不要求恰好等于区间的中点,但是 \(m\) 还是必
须满足 \(l \le m < r\) 的。不难发现在广义的线段树中,树的深度可以达到 \(O(n)\) 级别。
例如下面这棵树,就是一棵广义的线段树:
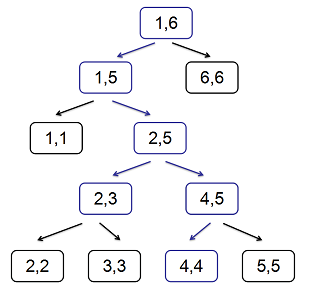
为了方便,我们按照先序遍历给线段树上所有的节点标号,例如在上图中,\([2, 3]\) 的标号是 \(5\),\([4, 4]\) 的标号是 \(9\),不难发现在 \([1, n]\) 上建立的广义线段树,它共有着 \(2n − 1\) 个节点。
考虑把线段树上的定位区间操作 \((\)就是打懒标记的时候干的事情\()\) 移植到广义线段树上,可以发现在广义的线段树上还是可以用传统的线段树上的方法定位区间的,例如在上图中,蓝色节点和蓝色边就是在定位区间 \([2, 4]\) 时经过的点和边,最终定位到的点是 \([2, 3]\) 和 \([4, 4]\)。
输入格式
第一行输入一个整数 \(n\)。
接下来一行包含 \(n - 1\) 个空格隔开的整数:按照标号递增的顺序,给出广义线段树上所有非叶子 节点的划分位置 \(m\)。不难发现通过这些信息就能唯一确定一棵 \([1, n]\) 上的广义线段树。
接下来一行输入一个整数 \(m\)。
之后 \(m\) 行每行输入三个整数 \(u, l, r\ (1 \le u \le 2n − 1, 1 \le l \le r \le n)\),表示一组询问。
输出格式
对于每组询问,输出一个整数表示答案。
数据范围与提示
对于 \(100\%\) 的数据,保证 \(2\leq n\leq 10^5, m\leq 10^5\)。
首先线段树上询问\([l,r]\)所访问到的节点就是\(l-1\)所代表的的节点往上走,访问所以经过节点的右儿子(如果有的话);以及\(r+1\)所代表的节点往上走访问的左儿子。直到两个点走到\(lca\)处停止(\(lca\)处不访问)。
这样我们就可以用倍增,来计算某个点到其某个祖先路径上所有的 左/右 儿子的 个数/到根距离和。问题是怎么求这些点到给定点\(u\)的\(lca\)。
我们假设\(l-1\)所代表的节点为\(v\)(处理右边的同理)。我们先求出\(u\)与\(v\)的\(lca\)记为\(LCA\)。然后我们分两段统计右儿子\((v,LCA]\),\((LCA,f)\)。前一段的右儿子与\(u\)的\(lca\)就是\(LCA\),后一段的\(lca\)就是每个右儿子的父亲。当然如果\(LCA\)是\(f\)的祖先那么只统计\((v,f)\)
然后有个坑点,比如说某个右儿子\(son\),\(LCA\)是\(son\)的祖先,\(son\)是\(u\)的祖先(可以发现,最多只有一个这样的\(son\)),那么\(u\)到\(son\)的距离被多算了\(2\),减去就好了。
代码:
#include<bits/stdc++.h>
#define ll long long
#define N 400005
using namespace std;
inline int Get() {int x=0,f=1;char ch=getchar();while(ch<'0'||ch>'9') {if(ch=='-') f=-1;ch=getchar();}while('0'<=ch&&ch<='9') {x=(x<<1)+(x<<3)+ch-'0';ch=getchar();}return x*f;}
int n,m;
struct road {int to,nxt;}s[N<<1];
int h[N],cnt;
void add(int i,int j) {s[++cnt]=(road) {j,h[i]};h[i]=cnt;}
int Div[N];
int tot,div_tim;
int ls[N],rs[N];
int L[N],R[N],Mid[N];
int pos[N],dep[N];
int fa[N][20];
int lsum[N][20],rsum[N][20];
int lsize[N][20],rsize[N][20];
void dfs(int &v,int l,int r,int f) {
v=++tot;
fa[v][0]=f;
dep[v]=dep[f]+1;
for(int i=1;i<=18;i++) fa[v][i]=fa[fa[v][i-1]][i-1];
L[v]=l,R[v]=r;
if(l==r) {
pos[l]=v;
return ;
}
int mid=Div[++div_tim];
Mid[v]=mid;
dfs(ls[v],l,mid,v),dfs(rs[v],mid+1,r,v);
}
int lca(int a,int b) {
if(dep[a]<dep[b]) swap(a,b);
for(int i=18;i>=0;i--)
if(fa[a][i]&&dep[fa[a][i]]>=dep[b])
a=fa[a][i];
if(a==b) return a;
for(int i=18;i>=0;i--)
if(fa[a][i]!=fa[b][i])
a=fa[a][i],b=fa[b][i];
return fa[a][0];
}
int Get_dis(int a,int b) {return dep[a]+dep[b]-2*dep[lca(a,b)];}
int Find_below(int v,int f) {
for(int i=18;i>=0;i--)
if(fa[v][i]&&dep[fa[v][i]]>dep[f])
v=fa[v][i];
return v;
}
void Findl(int v,int f,ll &size,ll &sum) {
for(int i=18;i>=0;i--) {
if(fa[v][i]&&dep[fa[v][i]]>=dep[f]) {
size+=lsize[v][i];
sum+=lsum[v][i];
v=fa[v][i];
}
}
}
void Findr(int v,int f,ll &size,ll &sum) {
for(int i=18;i>=0;i--) {
if(fa[v][i]&&dep[fa[v][i]]>=dep[f]) {
size+=rsize[v][i];
sum+=rsum[v][i];
v=fa[v][i];
}
}
}
ll cal_l(int v,int u,int f) {
int Lca=lca(v,u);
ll ans=0;
ll belz=0,bels=0;
ll upz=0,ups=0;
Findr(v,dep[f]>dep[Lca]?f:Lca,belz,bels);
if(dep[Lca]>dep[f]) {
Findr(Lca,f,upz,ups);
}
ans=bels+belz*dep[u]-2*belz*dep[Lca]+ups+upz*dep[u]-2*(ups-upz);
if(Find_below(u,Lca)==rs[Lca]&&dep[Lca]>=dep[f]) ans-=2;
return ans;
}
ll cal_r(int v,int u,int f) {
int Lca=lca(v,u);
ll ans=0;
ll belz=0,bels=0;
ll upz=0,ups=0;
Findl(v,dep[f]>dep[Lca]?f:Lca,belz,bels);
if(dep[Lca]>dep[f]) {
Findl(Lca,f,upz,ups);
}
ans=bels+belz*dep[u]-2*belz*dep[Lca]+ups+upz*dep[u]-2*(ups-upz);
if(Find_below(u,Lca)==ls[Lca]&&dep[Lca]>=dep[f]) ans-=2;
return ans;
}
void solve(int u,int l,int r) {
ll ans=0;
if(l==1&&r==n) {
cout<<dep[u]-1<<"\n";
} else {
int LCA;
if(l==1||r==n) LCA=1;
else LCA=lca(pos[l-1],pos[r+1]);
if(l==1&&r>=Mid[1]) ans+=Get_dis(u,ls[1]);
if(r==n&&l<=Mid[1]+1) ans+=Get_dis(u,rs[1]);
if(l!=1) ans+=cal_l(pos[l-1],u,Find_below(pos[l-1],LCA));
if(r!=n) ans+=cal_r(pos[r+1],u,Find_below(pos[r+1],LCA));
cout<<ans<<"\n";
}
}
int main() {
n=Get();
for(int i=1;i<n;i++) Div[i]=Get();
int rt;
dep[1]=1;
dfs(rt,1,n,0);
for(int i=2;i<=tot;i++) {
if(i==ls[fa[i][0]]) {
rsum[i][0]=dep[rs[fa[i][0]]],rsize[i][0]=1;
} else {
lsum[i][0]=dep[ls[fa[i][0]]],lsize[i][0]=1;
}
}
for(int j=1;j<=18;j++) {
for(int i=1;i<=tot;i++) {
if(fa[i][j]) {
lsum[i][j]=lsum[i][j-1]+lsum[fa[i][j-1]][j-1];
lsize[i][j]=lsize[i][j-1]+lsize[fa[i][j-1]][j-1];
rsum[i][j]=rsum[i][j-1]+rsum[fa[i][j-1]][j-1];
rsize[i][j]=rsize[i][j-1]+rsize[fa[i][j-1]][j-1];
}
}
}
m=Get();
int u,l,r;
while(m--) {
u=Get(),l=Get(),r=Get();
solve(u,l,r);
}
return 0;
}

