【2010国家集训队】人员雇佣

Description

　　作为一个富有经营头脑的富翁，小L决定从本国最优秀的经理中雇佣一些来经营自己的公司。这些经理相互之间合作有一个贡献指数,（我们用Ei,j表示i经理对j经理的了解程度），即当经理i和经理j同时被雇佣时，经理i会对经理j做出贡献，使得所赚得的利润增加Ei,j。当然，雇佣每一个经理都需要花费一定的金钱Ai，对于一些经理可能他做出的贡献不值得他的花费，那么作为一个聪明的人，小L当然不会雇佣他。然而，那些没有被雇佣的人会被竞争对手所雇佣，这个时候那些人会对你雇佣的经理的工作造成影响，使得所赚得的利润减少Ei,j（注意：这里的Ei,j与上面的Ei,j是同一个）。
　　作为一个效率优先的人，小L想雇佣一些人使得净利润最大。你可以帮助小L解决这个问题吗？

Input

　　第一行有一个整数$N\leq1000$表示经理的个数。
　　第二行有N个整数$A_i$表示雇佣每个经理需要花费的金钱。
　　接下来的N行中一行包含$N$个数，表示$E_{i,j}$，即经理i对经理j的了解程度。（输入满足$E_{i,j}=E_{j,i}$）

Output

　　第一行包含一个整数，即所求出的最大值。

Sample Input

Sample Output

Hint

【数据规模和约定】
　　20%的数据中$N<=10$
　　50%的数据中$N<=100$
　　100%的数据中 $N<=1000$，$ E_{i,j}<=int, A_i<=int$

二元组关系的网络流。解方程的套路。

我们先假设雇佣了所有的人，却不付出代价，然后再减去最小割的代价。

$S$表示雇佣，$T$表示不雇佣。

观察下面的图。如果我们割了$a,b$，那么我们就少了$E_{i,j}$的价值；如果割了$a,d,f$，那么我们要付出$E_{i,j}$的代价，也就是减少了$3*E_{i,j}$的价值；同理割了$b,e,c$就减少了$3*E_{i,j}$的价值。割了$e,f$相当于$i,j$都不雇佣，减少$2*E_{i,j}$的代价。

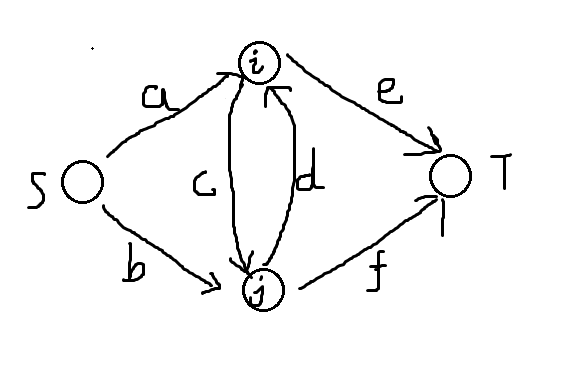
于是我们可以列出方程：

\[\begin{cases} a+b=E_{i,j}\\ e+f=2E_{i,j}\\ a+d+f=3E_{i,j}\\ b+c+e=3E_{i,j}\\ \end{cases} \]

解得：

\[\begin{cases} a=0\\ b=0\\ c=2E_{i,j}\\ d=2E_{i,j}\\ e=E_{i,j}\\ f=E_{i,j} \end{cases} \]

我们还要连$(S,i,V_i)$表示雇佣的代价。

代码：

#include<bits/stdc++.h>
#define ll long long
#define N 1005

using namespace std;
inline int Get() {int x=0,f=1;char ch=getchar();while(ch<'0'||ch>'9') {if(ch=='-') f=-1;ch=getchar();}while('0'<=ch&&ch<='9') {x=(x<<1)+(x<<3)+ch-'0';ch=getchar();}return x*f;}

int n;
struct road {
	int to,next;
	int flow;
}s[N*N<<2];
int h[N],cnt=1;
int cur[N];
void add(int i,int j,int f,int f2) {
	s[++cnt]=(road) {j,h[i],f};h[i]=cnt;
	s[++cnt]=(road) {i,h[j],f2};h[j]=cnt;
}
int S,T;
int dis[N]; 
queue<int>q;
bool bfs() {
	memset(dis,0x3f,sizeof(dis));
	q.push(S);
	dis[S]=0;
	while(!q.empty()) {
		int v=q.front();
		q.pop();
		for(int i=h[v];i;i=s[i].next) {
			int to=s[i].to;
			if(s[i].flow&&dis[to]>dis[v]+1) {
				dis[to]=dis[v]+1;
				q.push(to);
			}
		}
	}
	return dis[T]<1e9;
}

int dfs(int v,int maxf) {
	if(v==T) return maxf;
	int ret=0;
	for(int &i=cur[v];i;i=s[i].next) {
		int to=s[i].to;
		if(s[i].flow&&dis[to]==dis[v]+1) {
			int dlt=dfs(to,min(maxf,s[i].flow));
			s[i].flow-=dlt;
			s[i^1].flow+=dlt;
			ret+=dlt;
			maxf-=dlt;
			if(!maxf) return ret;
		}
	}
	return ret;
}

ll dinic() {
	ll ans=0;
	while(bfs()) {
		while(1) {
			memcpy(cur,h,sizeof(h));
			int tem=dfs(S,1e9);
			if(!tem) break;
			ans+=tem;
		}
	}
	return ans;
}

ll e[N][N];
ll a[N];
ll sum;
int main() {
	n=Get();
	for(int i=1;i<=n;i++) a[i]=Get();
	for(int i=1;i<=n;i++)
		for(int j=1;j<=n;j++)
			e[i][j]=Get(),sum+=e[i][j];
	T=n+1;
	for(int i=1;i<=n;i++) {
		ll tem=0;
		for(int j=1;j<=n;j++) tem+=e[i][j];
		add(i,T,tem,0);
		add(S,i,a[i],0);
		for(int j=i+1;j<=n;j++) {
			add(i,j,2*e[i][j],2*e[i][j]);
		}
	}
	ll maxflow=dinic();
	cout<<sum-maxflow;
	
	return 0;
}

posted @ 2019-03-28 18:35 hec0411 阅读(208) 评论(0) 编辑收藏举报

刷新页面返回顶部

hec0411

【2010国家集训队】人员雇佣