数据结构-二叉树相关代码
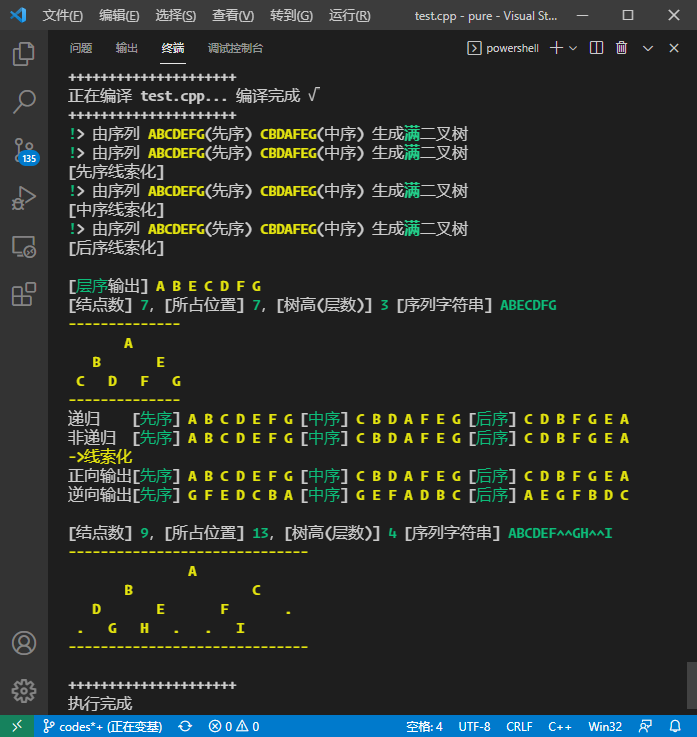
可用 g++ test.cpp -otest; ./test 命令运行
测试文件
/*
* @Description: test.cpp 文件
* @Version: 1.0
* @Author: hccodec
* @Date: 2021-09-08 17:02:41
* @LastEditors: hccodec
* @LastEditTime: 2021-09-15 16:03:34
*/
#include <iostream>
using namespace std;
#include "BiTree.cpp"
const char *args[] = {"先序", "中序", "后序", "层序"};
/** 测试输出
* @param {BiTree} *T 递归输出所用二叉树
* @param {ElemType} * 存放原结果及三种线索化结果的数组
* @return {*}
*/
void TestOutput(BiTree *T, ElemType **res) {
printf("\e[0m递归 "); for (int i = 1; i <= 3; i++) { printf("\e[0m[\e[32m%s\e[0m] \e[33m", args[i - 1]); T->PrintRecursion(i); } cout << endl;
printf("\e[0m非递归 "); for (int i = 1; i <= 3; i++) { printf("\e[0m[\e[32m%s\e[0m] \e[33m", args[i - 1]); res[i - 1] = T->GetOutput(i, true); } cout << endl;
}
void TestInThread(BiTree **Trees) {
printf("->线索化\n");
printf("\e[0m正向输出");
for (int i = 0; i < 3; i++) { printf("\e[0m[\e[32m%s\e[0m] \e[33m", args[i]); Trees[i + 1]->InOrder(); } cout << endl;
printf("\e[0m逆向输出");
for (int i = 0; i < 3; i++) { printf("\e[0m[\e[32m%s\e[0m] \e[33m", args[i]); Trees[i + 1]->RevInOrder(); } cout << endl;
}
void TestPrePost(BiTree **Trees) {
printf("->\e[1;36m前驱\e[1;35m后继\n");
for (int i = 1; i <= 3; i++)
{
BiTree *Tmp = Trees[i]; TNode *p, *q = Tmp->FirstNode();
printf("\e[0m[\e[32m%s\e[0m] ", args[i - 1]);
for (int j = 0; j < Tmp->count; j++) {
p = q;
if (Tmp->PreNode(p)) printf("\e[1;36m%2c\e[0;33m", Tmp->PreNode(p)->data);
else printf("\e[0;36m .\e[0;33m");
printf("%2c", p->data);
if (Tmp->NextNode(p)) printf("\e[1;35m%2c\e[0;33m", Tmp->NextNode(p)->data);
else printf("\e[0;35m .\e[0;33m");
cout << " |";
q = Tmp->NextNode(q);
}
cout << "\b " << endl;
}
}
void TestSimiliar(BiTree *A, BiTree *B) {
printf("两树%s相似\n", A->IsSimiliar(A->T, B->T) ? "" : "不");
}
void test()
{
ElemType *A = (char*)"ABCDEFG";
ElemType *B = (char*)"CBDAFEG";
// ElemType *A = (char*)"ABCDEFGHI", *B = (char*)"BCAEDGHFI";
BiTree *T, *PreBiTree, *InBiTree, *PostBiTree;
// Tree *Tmp = (new BiTree(T))->InThread(1);
T = new BiTree(A, B);
PreBiTree = (new BiTree(A, B))->InThread(1);
InBiTree = (new BiTree(A, B))->InThread(2);
PostBiTree = (new BiTree(A, B))->InThread(3);
BiTree *Trees[4] = {T, PreBiTree, InBiTree, PostBiTree};
ElemType *res[4]; // 存放结果序列的数组
printf("\n\e[0m[\e[32m%s\e[0m输出] \e[33m", args[3]); res[3] = T->GetOutput(4, true); cout << "\e[0m" << endl; T->PrettyPrint(true);
/////////////////////////////////////////////////////////////
TestOutput(T, res);
TestInThread(Trees);
// TestPrePost(Trees);
cout << "\e[0m";
return;
}
int main(int argc, char const *argv[])
{
test();
cout << endl;
(new BiTree())->PrettyPrint(true);
return 0;
}
二叉树源文件
/*
* @Description: 二叉树类文件
* @Version: 1.0
* @Author: hccidec
* @Date: 2021-09-14 20:10:46
* @LastEditors: hccodec
* @LastEditTime: 2021-09-15 16:01:33
*/
#include <iostream>
#include <cstring>
#include <cmath>
#include <queue>
#include <stack>
using namespace std;
#define ElemType char
class Util {
public:
class MyException
{
public:
protected:
int code;
};
static ElemType *BubbleSort(ElemType const X[], int const n) {
return NULL;
ElemType tmp; ElemType *res = (char*)X;
printf("%s %d ", res, n);
for (int i = 0; i < n; i++)
for (int j = 0; j < n - 1; j++)
if (res[j] > res[j + 1]) {
tmp = res[j];
printf(" res[%d] {%c} = res[%d] {%c}", j, res[j], j + 1, res[j + 1]);
res[j] = res[j + 1];
res[j + 1] = tmp;
}
return res;
}
};
struct TNode { ElemType data; TNode *lchild, *rchild, *parent; int ltag, rtag; };
bool print = true;
class BiTree
{
public:
TNode *T = NULL;
int height = 0, width = 0, count = 0, size = 0; // 树的宽、高、节点数和所占位置总数
char *repr_string;
int mode = 0; // 0 表示未被线索化, 1-3 分别表示 先序线索化、中序线索化、后序线索化
BiTree() { Reset(); GetInfo(); }
BiTree(ElemType const *Pre, ElemType const *In, bool bias = 0) {
if (Util::BubbleSort(Pre, strlen(Pre)) - Util::BubbleSort(In, strlen(In)) != 0) {
printf("输入序列\e[32m!\e[0m> 序列 \e[33m%s\e[0m(先序) 与序列 \e[33m%s\e[0m(中序)不合法", Pre, In);
Reset();
}
else {
if (print) printf("\e[32m!\e[0m> 由序列 \e[33m%s\e[0m(先序) \e[33m%s\e[0m(中序)", Pre, In);
// printf("Pre = %s, In = %s, 1 = %d, nPre = %d, 1 = %d, nIn = %d\n", Pre, In, 1, nPre, 1, nIn);
try {
T = PreInCre(Pre, In, 0, strlen(Pre) - 1, 0, strlen(In) - 1); count++;
// throw 0.5;
}
catch(double) {
cerr << "\n\e[1;31m发生异常\e[0m"; exit(0);
}
}
GetInfo();
if (print) printf(" 生成%s\e[0m二叉树\n", IsComplete() ? (IsFull() ? "\e[1;32m满\e[0m" : "完全") : "普通");
}
BiTree(BiTree *T) { this->T = T->T; this->mode = T->mode; GetInfo(); }
/** 获取结点
* @param {ElemType} e 所获结点的数据域的值
* @return {*}
*/
TNode * GetNode(ElemType e) {
queue<TNode*> q; TNode *p = T; q.push(p);
while(!q.empty()) {
if (q.front()->data == e) return q.front();
else {
p = q.front();
if (ExistChild(p, 0)) q.push(p->lchild);
if (ExistChild(p, 1)) q.push(p->rchild);
q.pop();
}
}
printf("未找到结点 %c\n", e);
return NULL;
}
void GetInfo () {
queue<ElemType> q; queue<TNode*> _q; q.push(T->data); _q.push(T); TNode *p = FirstNode(T); int tmp = 0;
while(tmp < count - 1) {
p = _q.front();
if (ExistChild(p, 0)) { _q.push(p->lchild); q.push(p->lchild->data); tmp++; }
else { q.push('^'); _q.push(NewNode('^')); }
if (ExistChild(p, 1)) { _q.push(p->rchild); q.push(p->rchild->data); tmp++; }
else { q.push('^'); _q.push(NewNode('^')); }
_q.pop();
}
size = q.size();
height = floor(log2(size + 1)) + (log2(size + 1) - floor(log2(size + 1)) == 0 ? 0 : 1);
repr_string = new ElemType[size]; for (int i = 0; i < size; i++) { repr_string[i] = q.front(); q.pop(); }
}
/** 创建新结点
* @param {ElemType} e 要创建的结点的数据域的值
* @return {*}
*/
TNode * NewNode(ElemType e) {
TNode *p;
try{
p = new(nothrow) TNode;
}catch(bad_alloc &memExp) {
cerr << memExp.what() << endl;
printf("出现异常");
}
p->data = e;
p->lchild = p->rchild = p->parent = NULL;
p->ltag = p->rtag = 0;
return p;
}
/** 添加新结点
* @param {ElemType} target 其父结点
* @param {ElemType} e 要添加的内容
* @param {int} side 添加位置(左孩子为0,右孩子为1)
* @return {*}
*/
BiTree * AddNode(ElemType target, ElemType e, int side) {
TNode *p = GetNode(target);
TNode *q = NewNode(e);
return AddNode(p, q, side);
}
/** 添加新结点
* @param {TNode} *target 其父结点
* @param {ElemType} e 要添加的内容
* @param {int} side 添加位置(左孩子为0,右孩子为1)
* @return {*}
*/
BiTree * AddNode(TNode *target, ElemType e, int side) {
TNode *q = NewNode(e);
return AddNode(target, q, side);
}
/** 添加新结点
* @param {TNode} *target 其父结点
* @param {TNode} *e 要添加的内容
* @param {int} side 添加位置(左孩子为0,右孩子为1)
* @return {*}
*/
BiTree * AddNode(TNode *target, TNode *e, int side) {
if (!target) { printf("\e[1;31m要添加的位置不存在,无法添加结点‘%c’\e[0m\n", e->data); return this; }
// if (mode != 0) { printf("\e[1;31m暂时不支持向线索化的树\e[0m\n"); return this; }
if(ExistChild(target, side)) {
printf("\e[1;31m结点‘%c’要插入的位置'%c'已有%s结点\e[0m\n", e->data, target->data, side == 0 ? "左" : (side == 1 ? "右" : "×")); return this;}
if (side != 0 && side != 1) { printf("\e[1;31m添加位置不合法,添加位置(左孩子为0,右孩子为1)\e[0m\n"); return this;}
if (side == 0) { target->lchild = e;}
else if (side == 1) { target->rchild = e;}
count++; e->parent = target;
return this;
}
/** 更改指定结点
* @param {ElemType} target 其父结点
* @param {ElemType} e 要添加的内容
* @param {int} side 添加位置(左孩子为0,右孩子为1)
* @return {*}
*/
BiTree * ChangeNode(ElemType target, ElemType e) {
TNode *p = GetNode(target);
return ChangeNode(p, e);
}
/** 更改指定结点
* @param {TNode} *target 其父结点
* @param {ElemType} e 要添加的内容
* @param {int} side 添加位置(左孩子为0,右孩子为1)
* @return {*}
*/
BiTree * ChangeNode(TNode *target, ElemType e) {
if (!target) { printf("\e[1;31m未找到该结点,无法添加\e[0m\n"); return this; }
target->data = e;
return this;
}
/** 判断是否存在子节点
* @param {TNode} *p 要判断的结点
* @param {int} side 0表示左,1表示右
* @return {*}
*/
bool ExistChild(TNode *p, int side) {
if (!p) { printf("结点为空 "); return false; }
switch (side) {
case 0: return p->lchild && p->ltag == 0;
case 1: return p->rchild && p->rtag == 0;
default: printf("程序有误请检查"); return false;
}
}
void Reset()
{
T = NewNode('A'); count++; this
->AddNode('A', 'B', 0)
->AddNode('A', 'C', 1)
->AddNode('B', 'D', 0)
->AddNode('B', 'E', 1)
->AddNode('C', 'F', 0)
->AddNode('D', 'G', 1)
->AddNode('F', 'I', 1)
->AddNode('E', 'H', 0);
}
/** 首结点
* @param {TNode} *p
* @return {*}
*/
TNode * FirstNode(TNode *p = NULL) {
if (!p) p = T;
switch (mode) {
case 1: return p;
case 2: while (p->ltag == 0) { p = p->lchild; } return p;
case 3: while (true) { if (p->ltag == 0) p = p->lchild; else if (p->rtag == 0) p = p->rchild; else return p; } break;
default: break;
}
return T;
}
/** 尾结点
* @param {TNode} *p
* @return {*}
*/
TNode * LastNode(TNode *p = NULL) {
if (!p) p = T;
switch (mode) {
case 1: while (true) { if (p->rtag == 0) p = p->rchild; else if (p->ltag == 0) p = p->lchild; else return p; }
case 2: while (p->rtag == 0) { p = p->rchild; } return p;
case 3: return p;
default: break;
}
return NULL;
}
/** 前驱结点
* @param {TNode} *p
* @return {*}
*/
TNode * PreNode(TNode *p) {
switch (mode) {
case 1:
if (!p->parent) return NULL;
else if (p->parent->lchild == p) return p->parent; // 如果是左节点
else if (p->parent->ltag == 1) return p->parent;
else return LastNode(p->parent->lchild); //左节点存在,返回左子树最后一个结点
case 2:
if (p->ltag == 0) return LastNode(p->lchild);
return p->lchild;
case 3:
if (p->ltag == 0 && p->rtag == 0) return p->rchild;
return p->lchild;
default: break;
}
return NULL;
}
/** 后继结点
* @param {TNode} *p
* @return {*}
*/
TNode * NextNode(TNode *p) {
switch (mode) {
case 1:
if (p->rtag == 0 && p->ltag == 0) return p->lchild;
return p->rchild;
case 2:
if (p->rtag == 0) return FirstNode(p->rchild);
return p->rchild;
case 3:
if (!p->parent) return NULL;
else if (p->parent->rchild == p) return p->parent;
else if (p->parent->rtag == 1) return p->parent;
else return FirstNode(p->parent->rchild);
default: break;
}
return NULL;
}
void InOrder() {
for (TNode *p = FirstNode(T); p; p = NextNode(p)) printf("%c ", p->data);
}
void RevInOrder() {
for (TNode *p = LastNode(T); p; p = PreNode(p)) printf("%c ", p->data);
}
/** 递归打印
* @param {int} type 1-3分别表示【先序、中序、后序】
* @return {*}
*/
void PrintRecursion(int type)
{
switch (type)
{
case 1:
return _Print1(T);
case 2:
return _Print2(T);
case 3:
return _Print3(T);
default:
printf("\e[1;31m[PrintRecursion] 类型错误,请输入正确类型:\e[0;33m1-3分别表示【先序、中序、后序】\e[0m");
}
}
/** 非递归打印
* @param {int} type 1-4 分别表示【先序、中序、后序、层序】
* @param {bool} out out = true 表示输出
* @return {*}
*/
ElemType * GetOutput(int type, bool out = false)
{
if (mode != 0) {
printf("非递归打印不支持已被线索化的二叉树。因代码直接访问 lchild 和 rchild 指针而未对其指向左右孩子或指向线索化的前驱后继这两种情况进行判断。\n");
// printf("(%d) ", mode);
return NULL;
}
TNode *p = T, *pre = NULL; queue<ElemType> q;
stack<TNode *> s; // 辅助栈
int tag = 0; // 入栈tag=0;出栈tag=1
switch (type)
{
case 1:
while (p || !s.empty())
if (p) { if (out) printf("%c ", p->data); q.push(p->data); s.push(p); p = ExistChild(p, 0) ? p->lchild : NULL; }
else { p = s.top(); p = ExistChild(p, 1) ? p->rchild : NULL; s.pop(); }
break;
case 2:
while (p || !s.empty())
if (p) { s.push(p); p = ExistChild(p, 0) ? p->lchild : NULL; }
else
{ p = s.top(); if (out) printf("%c ", p->data); q.push(p->data); s.pop(); p = ExistChild(p, 1) ? p->rchild : NULL; }
break;
case 3:
while (p || !s.empty())
{ // 以下提供了未线索化和已线索化两种实现方式的代码示例
if (mode == 0)
{
if (tag == 0) { // tag表示非递归遍历的当前操作是入栈(tag=0)还是出栈(tag=1)
// 若为入栈操作则左子结点优先于右子结点入栈
if (p->lchild) { s.push(p); pre = p; p = p->lchild; }
else if (p->rchild) { s.push(p); pre = p; p = p->rchild; }
// 否则为叶子结点。将其入栈并通过标记tag=1控制下一操作改为出栈
else { if (out) printf("%c ", p->data); q.push(p->data); pre = p; p = s.top(); tag = 1; }
}
else {
// 出栈,仅需判断当前结点(栈顶元素)是否有未被遍历的右子结点
if (!p->rchild) { pre = p; if (out) printf("%c ", p->data); q.push(p->data); s.pop(); p = s.top(); } // 没有右子结点
else {
if (pre == p->rchild) { if (out) printf("%c ", p->data); q.push(p->data); pre = p; s.pop(); if (!s.empty()) p = s.top(); else break; }
else { pre = p; p = p->rchild; tag = 0; }
}
}
}
else
{
if (p) { s.push(p); p = ExistChild(p, 0) ? p->lchild : NULL; }
else {
p = s.top();
if (ExistChild(p, 1) && p->rchild != pre) p = p->rchild;
else {
p = s.top();
if (out) printf("%c ", p->data);
pre = p;
p = NULL;
s.pop();
}
}
}
}
break;
case 4:
return _Print4(T, true);
default:
printf("检查type变量,type 1-4 分别表示【先序、中序、后序、层序】");
break;
}
int size = q.size();
ElemType *res = new ElemType[size + 1];
for (int i = 1; i <= size; i++)
{
res[i] = q.front();
q.pop();
}
return res;
}
TNode * FindPreByPointer(ElemType e, int type) {
TNode *pre = NULL;
switch (type)
{
case 1:
_FindPreByPointer1(T, e, pre);
break;
case 2:
_FindPreByPointer2(T, e, pre);
break;
case 3:
_FindPreByPointer3(T, e, pre);
break;
default:
printf("\e[1;31m类型错误,请输入正确类型:\e[0;33m1-4分别表示【先序、中序、后序、层序】\e[0m");
break;
}
return final;
}
/** 线索化
* @param {int} type 1-3分别表示【先序、中序、后序】
* @return {*}
*/
BiTree * InThread(int type) {
TNode *pre = NULL;
switch (type)
{
case 1:
if (print) printf("[先序线索化]\n"); _InThread1(T, pre);
mode = 1;
break;
case 2:
if (print) printf("[中序线索化]\n"); _InThread2(T, pre);
mode = 2;
break;
case 3:
if (print) printf("[后序线索化]\n"); _InThread3(T, pre);
mode = 3;
break;
default:
printf("\e[1;31m类型错误,请输入正确类型:\e[0;33m1-3分别表示【先序、中序、后序】\e[0m\n");
mode = type;
break;
}
//关于该 if 语句:分析线索化过程知,先序(根左右)和中序(左根右)的尾结点必再无右子结点
if (pre) if (!(pre->rchild && pre->rtag == 0)) pre->rtag = 1;
return this;
}
/** 去线索化
* @param {*}
* @return {*}
*/
BiTree * UnThread() {
if (mode == 0) return this;
mode = 0;
_UnThread(T);
return this;
}
void _UnThread(TNode *T) {
if (!T) return;
if (T->ltag == 0) _UnThread(T->lchild);
if (T->ltag == 1) { T->lchild = NULL; T->ltag = 0; }
if (T->rtag == 1) { T->rchild = NULL; T->rtag = 0; }
if (T->rtag == 0) _UnThread(T->rchild);
}
/** 按格式打印当前树,支持线索化树
* @param {TNode} *T 根结点
* @return {*}
*/
BiTree * PrettyPrint(bool printinfo = false, TNode *T = NULL) {
if (!T) T = this->T;
else {
queue<ElemType> q; queue<TNode*> _q; q.push(T->data); _q.push(T); TNode *p = FirstNode(T); int tmp = 0;
while(tmp < count - 1) {
p = _q.front();
if (ExistChild(p, 0)) { _q.push(p->lchild); q.push(p->lchild->data); tmp++; }
else { q.push('^'); _q.push(NewNode('^')); }
if (ExistChild(p, 1)) { _q.push(p->rchild); q.push(p->rchild->data); tmp++; }
else { q.push('^'); _q.push(NewNode('^')); }
_q.pop();
}
size = q.size();
height = floor(log2(size + 1)) + (log2(size + 1) - floor(log2(size + 1)) == 0 ? 0 : 1);
repr_string = new ElemType[size]; for (int i = 0; i < size; i++) { repr_string[i] = q.front(); q.pop(); }}
int i = 0, j = 0;
if (printinfo) printf("[结点数] \e[32m%d\e[0m,[所占位置] \e[32m%d\e[0m,[树高(层数)] \e[32m%d\e[0m [序列字符串] \e[32m%s\e[0m \n\e[33m", count, size, height, repr_string);
for (int i = 0; i < 2 * pow(2, height - 1) - 1; i++) printf("--"); cout << endl;
for (i = 1, j = 1; i <= size; i++) {
if (i == pow(2, j - 1)) { for (int k = 0; k < pow(2, height - j) - 1; k++) printf(" "); } // 行前空格(判据:当前是否为行首)
if (repr_string[i - 1] == '^') printf(" ."); else printf("%2c", repr_string[i - 1]);
if (i == pow(2, j) - 1) { cout << endl; j++; } // 换行(判据:当前是否为上一行行尾)
else{
for (int k = 1; k < pow(2, height - j + 1); k++) printf(" ");
} //行中空格
}
if (i != pow(2, j - 1)) cout << endl;
for (int i = 0; i < 2 * pow(2, height - 1) - 1; i++) printf("--");
printf("\e[0m\n");
return this;
}
int GetHeight(TNode *T = NULL, bool print = false) {
if (!T) { if (this->T) T = this->T; } else return 0;
queue<TNode*> q;
TNode *p = T, *last = T; int level = 0;
q.push(p); if (print) cout << "\n";
while (!q.empty())
{
if (print) cout << "[";
p = q.front();
if (ExistChild(p, 0)) q.push(p->lchild);
if (ExistChild(p, 1)) q.push(p->rchild);
if (p == last) { if (print) printf("(到%c)", last->data); level++; last = q.back();}
q.pop();
if (print) { queue <TNode*> Q = q; while(!Q.empty()) { cout<<" "<<Q.front()->data; Q.pop(); } }
if (print) cout << "] ";
}
return level;
}
/** 递归方式实现根据先序和中序序列建立新二叉树
* @param {ElemType *} A 先序序列
* @param {ElemType *} B 中序序列
* @param {int} l1 先序 序列 首 结点下标
* @param {int} h1 先序 序列 尾 结点下标
* @param {int} l2 中序 序列 首 结点下标
* @param {int} h2 中序 序列 尾 结点下标
* @param {int} bias 数组指针偏移量,默认数组从下标 1 开始
* @param {bool} cover 是否覆盖原树,默认为false (不覆盖)
* @return {*}
*/
TNode * PreInCre(ElemType const * A, ElemType const * B, int l1, int h1, int l2, int h2, int bias = 0, bool cover = false) {
// printf("{{欲添加 A[%d] = %c}} l1=%d, l2=%d, h1=%d, h2=%d\n", l1, A[l1], l1, l2, h1, h2);
TNode *p;
try {
p = NewNode(A[l1]); // 根结点
}
catch (exception&) {
throw(33);
}
int i; for (i = l2; B[i] != p->data; i++); // 划分中序序列
// printf("%d:%c ", i, p->data);
int llen = i - l2, rlen = h2 - i;
// printf("{{添加 %c}} llen=%d, rlen=%d, l1=%d, l2=%d, h1=%d, h2=%d\n", p->data, llen, rlen, l1, l2, h1, h2);
if (llen) AddNode(p, PreInCre(A, B, l1 + 1, l1 + llen, l2, l2 + llen - 1), 0);
else p->lchild = NULL;
if (rlen) AddNode(p, PreInCre(A, B, h1 - rlen + 1, h1, h2 - rlen + 1, h2), 1);
else p->rchild = NULL;
return p;
}
/** 判断二叉树是否为完全二叉树
* @param {TNode} *T
* @return {*}
*/
bool IsComplete (TNode *T = NULL) {
if (!T) T = this->T;
queue<TNode*> q; TNode *p = T; q.push(p);
while(!q.empty()) {
p = q.front(); q.pop();
if (p) {
if (p->ltag == 0) q.push(p->lchild);
if (p->rtag == 0) q.push(p->rchild);
}
else while(!q.empty()) {
p = q.front(); q.pop();
if (p) return false;
}
}
return true;
}
/** 判断二叉树是否为满二叉树
* @param {TNode} *T
* @return {*}
*/
bool IsFull (TNode *T = NULL) {
return IsComplete() && count == size;
}
/** 判断两个二叉树是否相似
* @param {TNode} *T1
* @param {TNode} *T2
* @return {*}
*/
bool IsSimiliar(TNode *T1, TNode *T2) {
bool left = 0, right = 0;
if (!T1 && !T2) return true;
if (!T1 || !T2) return false;
left = IsSimiliar(ExistChild(T1, 0) ? T1->lchild : NULL, ExistChild(T2, 0) ? T2->lchild : NULL);
right = IsSimiliar(ExistChild(T1, 1) ? T1->rchild : NULL, ExistChild(T2, 1) ? T2->rchild : NULL);
return left && right;
}
private:
TNode *final = NULL; // 用土办法找到中序前驱的结果
// 递归打印 start //////////////////////////////
void _Print1(TNode *T)
{
if (T)
{
printf("%c ", T->data);
if (ExistChild(T, 0)) _Print1(T->lchild);
if (ExistChild(T, 1)) _Print1(T->rchild);
}
}
void _Print2(TNode *T)
{
if (T)
{
if (ExistChild(T, 0)) _Print2(T->lchild);
printf("%c ", T->data);
if (ExistChild(T, 1)) _Print2(T->rchild);
}
}
void _Print3(TNode *T)
{
if (T)
{
if (ExistChild(T, 0)) _Print3(T->lchild);
if (ExistChild(T, 1)) _Print3(T->rchild);
printf("%c ", T->data);
}
}
ElemType * _Print4(TNode *T, bool out = false)
{
queue<ElemType> q; // 存放最终结果的队列
queue<TNode *> _q; // 层序遍历的辅助队列
_q.push(T);
while (!_q.empty())
{
q.push(_q.front()->data);
if (ExistChild(_q.front(), 0)) _q.push(_q.front()->lchild);
if (ExistChild(_q.front(), 1)) _q.push(_q.front()->rchild);
_q.pop();
}
int size = q.size();
ElemType *res = new ElemType[size];
for (int i = 0; i < size; i++)
{
res[i] = q.front();
if (out) printf("%c ", q.front());
q.pop();
}
return res;
}
// 递归打印 end /////////////////////////////////
// 指针法找前驱 start ///////////////////////////
void _FindPreByPointer1(TNode *T, ElemType e, TNode *&pre)
{
if (mode == 0 && T)
{
if (T->data == e) final = pre; pre = T;
_FindPreByPointer1(T->lchild, e, pre);
_FindPreByPointer1(T->rchild, e, pre);
}
else if (mode != 0) { printf("\e[31m此二叉树已被线索化 "); }
}
void _FindPreByPointer2(TNode *T, ElemType e, TNode *&pre)
{
if (mode == 0 && T)
{
_FindPreByPointer2(T->lchild, e, pre);
if (T->data == e) final = pre; pre = T;
_FindPreByPointer2(T->rchild, e, pre);
}
else if (mode != 0) { printf("\e[31m此二叉树已被线索化 "); }
}
void _FindPreByPointer3(TNode *T, ElemType e, TNode *&pre)
{
if (mode == 0 && T)
{
_FindPreByPointer3(T->lchild, e, pre);
_FindPreByPointer3(T->rchild, e, pre);
if (T->data == e) final = pre; pre = T;
}
else if (mode != 0) { printf("\e[31m此二叉树已被线索化 "); }
}
// 指针法找前驱 end /////////////////////////////
// 线索化 start ////////////////////////////////
void _InThread1(TNode *T, TNode *&pre)
{
if (!T) return;
if (!T->lchild) { T->lchild = pre; T->ltag = 1; }
if (pre && !pre->rchild) { pre->rchild = T; pre->rtag = 1; }
pre = T; //printf("%c ", pre->data);
if (T->ltag == 0) _InThread1(T->lchild, pre);
if (T->rtag == 0) _InThread1(T->rchild, pre);
}
void _InThread2(TNode *T, TNode *&pre)
{
if (T)
{
_InThread2(T->lchild, pre);
if (!T->lchild) { T->lchild = pre; T->ltag = 1; }
if (pre && !pre->rchild) { pre->rchild = T; pre->rtag = 1; }
pre = T; //printf("%c ", pre->data);
_InThread2(T->rchild, pre);
}
}
void _InThread3(TNode *T, TNode *&pre)
{
if (!T) return;
_InThread3(T->lchild, pre);
_InThread3(T->rchild, pre);
if (!T->lchild) { T->lchild = pre; T->ltag = 1;
// printf("%c->lchild ==> %c\n", T->data, pre?pre->data:'+');
}
if (pre && !pre->rchild) { pre->rchild = T; pre->rtag = 1;
// printf("%c->rchild ==> %c\n", pre ? pre->data : '+', T->data);
}
// else { printf(" %c->lchild = %c,且 pre ", T->data, T->lchild ? T->lchild->data : '+'); pre ? printf("= %c\n", pre->data) : printf("不存在\n"); }
pre = T;
}
// 线索化代码区 end /////////////////////////////
};

 把二叉树的代码简单整理了一下,在此记录
把二叉树的代码简单整理了一下,在此记录

