201871030109-韩诚 实验二 个人项目
| 项目 | 内容 |
|---|---|
| 课程班级博客链接 | 班级博客 |
| 这个作业要求链接 | 作业要求 |
| 我的课程学习目标 | 1. 熟悉和掌握github的操作 2.增强自己的动手能力 |
| 这个作业在哪些方面帮助我实现学习目标 | 1. 更加熟练git的相关操作 2. 熟练Typora编辑器的使用方法 |
| 项目Github的仓库链接地址 | GitHub仓库链接 |
博客正文
任务一：
已按照作业要求，对四名同学的Blog作业点评链接
任务二：
详细阅读《构建之法》第1章、第2章，掌握PSP流程。（已完成）
| 任务内容 | 计划共完成需要的时间(min) | 实际完成需要的时间(min) |
|---|---|---|
| 计划 | 80 | 60 |
| 查阅相关资料 | 40 | 30 |
| 规划PSP流程 | 50 | 30 |
| 开发 | 600 | 720 |
| 实现问题求解 | 120 | 160 |
| 排错 | 100 | 130 |
| 报告 | 120 | 100 |
| 编写博客 | 60 | 70 |
| 上传代码 | 10 | 10 |
| 总结流程 | 30 | 20 |
任务三：
项目开发背景：
-
背包问题（Knapsack Problem，KP）是NP Complete问题，也是一个经典的组合优化问题，有着广泛而重要的应用背景。{０-1}背包问题（{0-1 }Knapsack Problem，{0-1}KP）是最基本的KP问题形式，它的一般描述为：从若干具有价值系数与重量系数的物品（或项）中，选择若干个装入一个具有载重限制的背包，如何选择才能使装入物品的重量系数之和在不超过背包载重前提下价值系数之和达到最大？
-
D{0-1} KP 是经典{ 0-1}背包问题的一个拓展形式，用以对实际商业活动中折扣销售、捆绑销售等现象进行最优化求解，达到获利最大化。D{0-1}KP数据集由一组项集组成，每个项集有3项物品可供背包装入选择，其中第三项价值是前两项之和，第三项的重量小于其他两项之和，算法求解过程中，如果选择了某个项集，则需要确定选择项集的哪个物品，每个项集的三个项中至多有一个可以被选择装入背包，D{0-1} KP问题要求计算在不超过背包载重量 的条件下，从给定的一组项集中选择满足要求装入背包的项，使得装入背包所有项的价值系数之和达到最大；D{0-1}KP instances数据集是研究D{0-1}背包问题时，用于评测和观察设计算法性能的标准数据集；动态规划算法、回溯算法是求解D{0-1}背包问题的经典算法。查阅相关资料，设计一个采用动态规划算法、回溯算法求解D{0-1}背包问题的程序，
功能设计
- 读入文件
- 将txt中的数据存入列表
- 动态规划法求解背包问题
- 画出关于重量与价值的散点图
设计实现：
- 重要代码：
{
int i,j;
for(i=0; i<=n; i++)
V[i][0]=0;
for(j=0; j<=C; j++)
V[0][j]=0;
for(i=0; i<=n-1; i++)
for(j=0; j<=C; j++)
if(j<w[i])
V[i][j]=V[i-1][j];
else
V[i][j]=max(V[i-1][j],V[i-1][j-w[i]]+v[i]);
j=C;
for(i=n-1; i>=0; i--)
{
if(V[i][j]>V[i-1][j])
{
x[i]=1;
j=j-w[i];
}
else
x[i]=0;
}
cout << "选中的物品时：" << endl;
for(i=0; i<n; i++)
cout << x[i];
cout << endl;
return V[n-1][C];
}
代码提交
- 代码已经上传到GitHub仓库。
实验截图
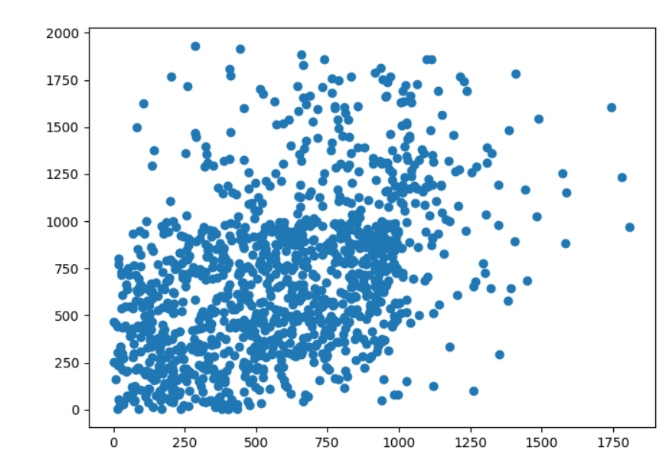
实验总结
- 这次的实验内容多并且复。在完成作业的过程中，我遇到了很多的困难，，在这个过程中，我通过上网查阅了很多的资料以及询问了同学，收获颇多。任务一和任务二没有什么难度，主要是任务三难度比想象中的困难及复杂，因为自己大的编程水平不是很好，完成了一部分的要求，加之网络的原因代码未能成功的上传到GitHub库里面，所以就没有按时完成，后续我会继续努力学习并完善，提高自己的编程水平。
