[BZOJ2127]happiness
Description
高一一班的座位表是个n*m的矩阵,经过一个学期的相处,每个同学和前后左右相邻的同学互相成为了好朋友。这学期要分文理科了,每个同学对于选择文科与理科有着自己的喜悦值,而一对好朋友如果能同时选文科或者理科,那么他们又将收获一些喜悦值。作为计算机竞赛教练的scp大老板,想知道如何分配可以使得全班的喜悦值总和最大。
Input
第一行两个正整数n,m。接下来是六个矩阵第一个矩阵为n行m列 此矩阵的第i行第j列的数字表示座位在第i行第j列的同学选择文科获得的喜悦值。第二个矩阵为n行m列 此矩阵的第i行第j列的数字表示座位在第i行第j列的同学选择理科获得的喜悦值。第三个矩阵为n-1行m列 此矩阵的第i行第j列的数字表示座位在第i行第j列的同学与第i+1行第j列的同学同时选择文科获得的额外喜悦值。第四个矩阵为n-1行m列 此矩阵的第i行第j列的数字表示座位在第i行第j列的同学与第i+1行第j列的同学同时选择理科获得的额外喜悦值。第五个矩阵为n行m-1列 此矩阵的第i行第j列的数字表示座位在第i行第j列的同学与第i行第j+1列的同学同时选择文科获得的额外喜悦值。第六个矩阵为n行m-1列 此矩阵的第i行第j列的数字表示座位在第i行第j列的同学与第i行第j+1列的同学同时选择理科获得的额外喜悦值。
Output
输出一个整数,表示喜悦值总和的最大值
Sample Input
1 2
1 1
100 110
1
1000
Sample Output
1210
Solution
二元组建图,2016集训队候选队论文题,详见《网络流的一些建图方法》但是网上好像找不到
对于每个人建一个点,然后类似于这样的连边:
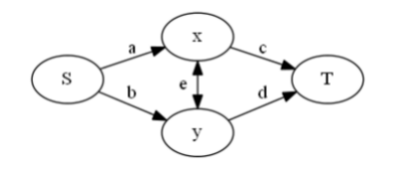
其中\(x,y\)为相邻的两个点,\(s,t\)为源汇点,那么枚举每人选文还是理有\(4\)种情况,然后可以根据损失情况列出方程:(注意这里忽略了每人选文还是理的单独的贡献)
解出来可得:
那么就可以得到建图了。
具体可以看代码的主函数部分,注意没有必要处理小数,直接整体乘2就好了。
#include<bits/stdc++.h>
using namespace std;
void read(int &x) {
x=0;int f=1;char ch=getchar();
for(;!isdigit(ch);ch=getchar()) if(ch=='-') f=-f;
for(;isdigit(ch);ch=getchar()) x=x*10+ch-'0';x*=f;
}
void print(int x) {
if(x<0) putchar('-'),x=-x;
if(!x) return ;print(x/10),putchar(x%10+48);
}
void write(int x) {if(!x) putchar('0');else print(x);putchar('\n');}
const int maxn = 2e5+10;
const int inf = 1e9;
int n,m,s,t,tot=1;
int head[maxn],vis[maxn],dis[maxn];
int l[102][102],r[102][102],a[102][102],b[102][102];
struct edge{int to,nxt,w;}e[maxn<<1];
void add(int u,int v,int w) {e[++tot]=(edge){v,head[u],w},head[u]=tot;}
void ins(int u,int v,int w) {add(u,v,w),add(v,u,0);}
void ins2(int u,int v,int w) {ins(u,v,w),ins(v,u,w);}
int bfs() {
memset(vis,0,(t+1)*10);
memset(dis,63,(t+1)*10);
queue<int > q;q.push(s);vis[s]=1;
while(!q.empty()) {
int now=q.front();q.pop();
for(int i=head[now];i;i=e[i].nxt)
if(!vis[e[i].to]&&e[i].w>0) {
dis[e[i].to]=dis[now]+1;
if(e[i].to==t) return 1;
q.push(e[i].to),vis[e[i].to]=1;
}
}return 0;
}
int dfs(int x,int f) {
if(x==t) return f;
int used=0;
for(int i=head[x];i;i=e[i].nxt)
if(e[i].w>0&&dis[e[i].to]==dis[x]+1) {
int d=dfs(e[i].to,min(f-used,e[i].w));
if(d>0) e[i].w-=d,e[i^1].w+=d,used+=d;
if(used==f) break;
}dis[x]=-1;return used;
}
int dinic() {
int flow=0;
while(bfs()) flow+=dfs(s,inf);
return flow;
}
int p(int x,int y) {return (x-1)*m+y;}
int main() {
read(n),read(m);int ans=0;
s=n*m+2,t=s+1;
for(int i=1,x;i<=n;i++)
for(int j=1;j<=m;j++) read(x),l[i][j]+=x<<1,ans+=x;
for(int i=1,x;i<=n;i++)
for(int j=1;j<=m;j++) read(x),r[i][j]+=x<<1,ans+=x;
for(int i=1,x;i<=n-1;i++)
for(int j=1;j<=m;j++)
read(x),l[i][j]+=x,l[i+1][j]+=x,a[i][j]+=x,ans+=x;
for(int i=1,x;i<=n-1;i++)
for(int j=1;j<=m;j++)
read(x),r[i][j]+=x,r[i+1][j]+=x,a[i][j]+=x,ans+=x;
for(int i=1,x;i<=n;i++)
for(int j=1;j<=m-1;j++)
read(x),l[i][j]+=x,l[i][j+1]+=x,b[i][j]+=x,ans+=x;
for(int i=1,x;i<=n;i++)
for(int j=1;j<=m-1;j++)
read(x),r[i][j]+=x,r[i][j+1]+=x,b[i][j]+=x,ans+=x;
for(int i=1;i<=n-1;i++)
for(int j=1;j<=m;j++) ins2(p(i,j),p(i+1,j),a[i][j]);
for(int i=1;i<=n;i++)
for(int j=1;j<=m-1;j++) ins2(p(i,j),p(i,j+1),b[i][j]);
for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) ins(s,p(i,j),l[i][j]),ins(p(i,j),t,r[i][j]);
write(ans-(dinic()>>1));
return 0;
}

