高斯消元

题目地址：戳这
上面那个是假的，数据太水,不过可以做做，来看看真题
这才是真题，数据比刚刚那道强多了

首先来看一道例题：

                                            

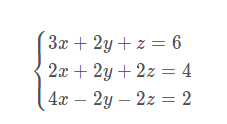
大家会觉得这到题是初中水题，看一眼就出来了，甚至有些人小学就会了。但是你们有没有想过如果有很多未知数的话怎么办能，手动消元？怎么可能。这复杂度太高了。于是便把目光转向了计算机。没错计算机可以很快的算出答案，但是计算机却没有人类这种思路，不能看题而来，而是去编写一个程序，来面对所有的问题。接下来就用这到题来讲讲高斯消元。

• 首先我们用矩阵来进行高斯消元。先把方程写成如下形式：

                                                    

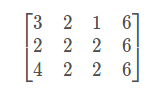
• 第二步对矩阵进行初等变换，初等变换包括如下几个操作：
  1.将某行同乘或同除一个非零实数
  2.将某一行加到另一行
• 第三步将矩阵变为上三角矩阵，就是把主对角线全变为1，主对角线下的数都变为零。形式如下：

                                                  

到这一步后就差不多没了，只要从最后一行往上带求出每个接并存入数组中就可以了

但是要注意一点，每次消元的时候找系数最大的那个。

代码如下

#include<bits/stdc++.h>
using namespace std;
double a[101][101];
int ABS(double x){
    return x<0?-x:x;
}
int main() {
    int n;
    scanf("%d",&n);
    for(int i=1; i<=n; i++)
        for(int j=1; j<=n+1; j++)
            scanf("%lf",&a[i][j]);
    for(int i=1; i<=n; i++) {
        int bj=i;
        for(int j=i+1; j<=n; j++)
            if(ABS(a[j][i])>ABS(a[bj][i]))
                bj=j;
        for(int j=1; j<=n+1; j++)
            swap(a[bj][j],a[i][j]);//找到系数最大的一个
        if(!a[i][i])
            continue;
        double p=a[i][i];
        for(int j=1;j<=n+1;j++)
            a[i][j]/=p;
        for(int j=1;j<=n;j++)
            if(i!=j){
                double o=a[j][i];
                for(int k=1;k<=n+1;k++)
                    a[j][k]-=a[i][k]*o;
            }
    }
    int bj2=0,bj1=0;
    for(int i=1; i<=n; i++) {
        int ans=0;
        for(int j=1; j<=n+1; j++) {
            if(!a[i][j])
                ans++;
        }
        if(ans==n&&a[i][n+1])
            bj2=1;
        
        if(ans==n+1)
            bj1=1;
    }
    if(bj2)
        printf("-1"),exit(0);//无解,因为在一行中的未知数系数为0，但结果不为0
    if(bj1)
        printf("0"),exit(0);//有无数解，因为在一行中的未知数系数为0，但结果为0。所以和未知数无关，答案一直为0，所以无论去未知数何值都满足条件
    for(int i=n-1; i>=1; i--)
        for(int j=i+1; j<=n; j++)
            a[i][n+1]-=a[j][n+1]*a[i][j];//往回带，求出答案
    for(int i=1; i<=n; i++) {
        if(a[i][n+1]==0)
            printf("x%d=0\n",i);
        else
            printf("x%d=%.2lf\n",i,a[i][n+1]);
    }
    return 0;
}