博客作业06--图
1.学习总结(2分)
1.1图的思维导图
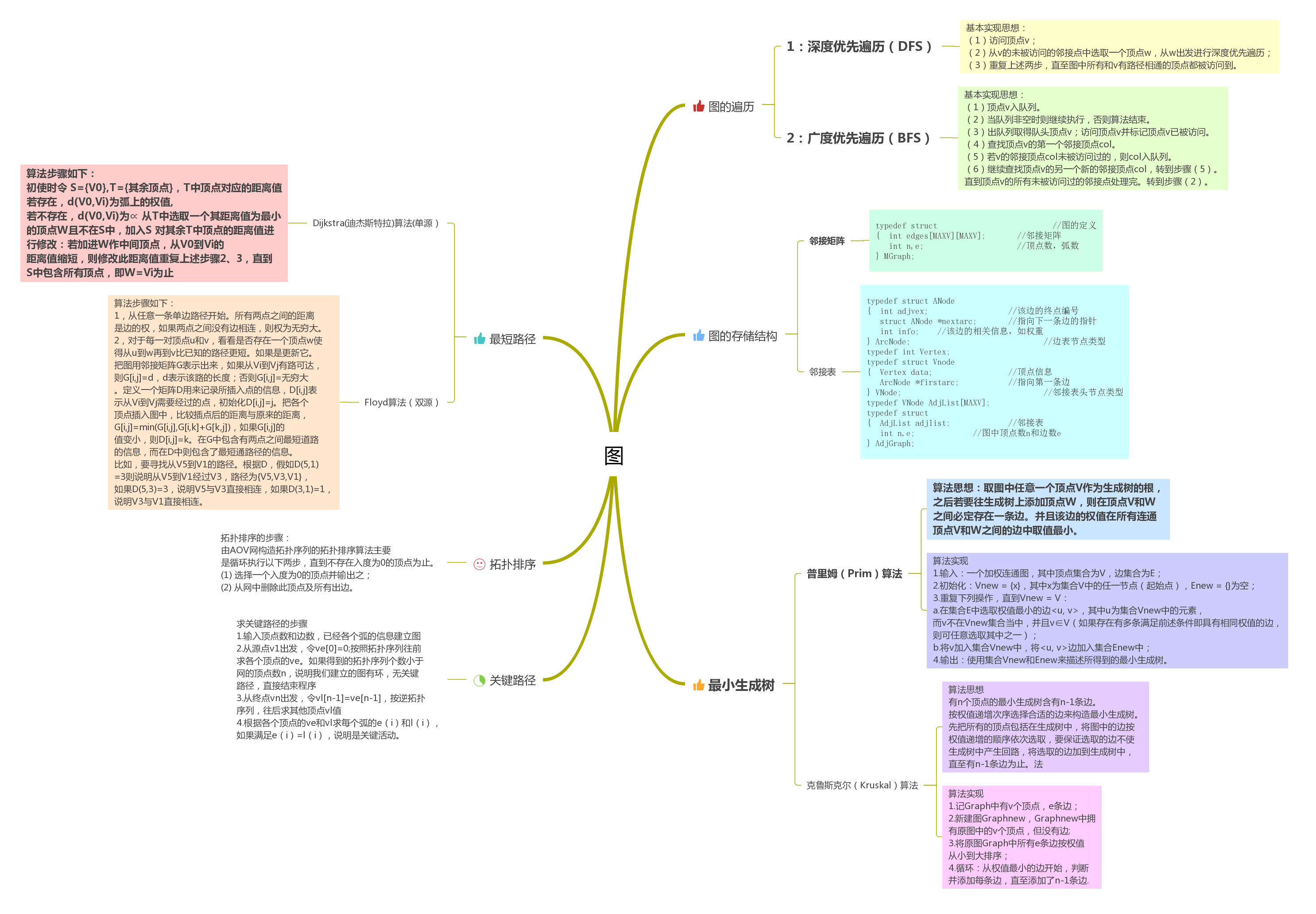
1.2 图结构学习体会
谈谈你对图结构中的几个经典算法学习体会。具体有:
深度和广度比较简单,一个递归,一个用队
Prim和Kruscal算法,理解的话还是可以理解,但是代码写起来就没那么顺畅
Dijkstra算法,比较复杂,至今还不是很懂
拓扑排序算法简单易懂,加一个入度然后用栈
2.PTA实验作业(4分)
2.1 题目1:7-3 六度空间
2.2 设计思路(伪代码或流程图)
建一个队,level标记层数,tail记录本层最后
一个结点,last判断本层是否遍历完
while(队不空)
{
出队头;
遍历本层,全部入队
遍历完一层,level++
更新last
if到6层了跳出循环
}
2.3 代码截图(注意,截图、截图、截图。代码不要粘贴博客上。不用用···语法去渲染)

2.4 PTA提交列表说明。

最大联通图段错误,这种大数据很难改,因为没办法测试,只能把遍历的条件那里初值或者满足条件改一下,一个个试过去,运气好就试出来了
2.1 题目2:7-6 修建道路
2.2 设计思路(伪代码或流程图)
初始化图结构,将已经修好的路的长度置为0
for(i=1 to n)
第i个点到已经标记点的集合的距离最小且这个点还没有被标记
index记录下一个将被标记的点
更新sum,计算要修的路的长度
for(i=1 to n)
更新最短距离
2.3 代码截图(注意,截图、截图、截图。代码不要粘贴博客上。不用用···语法去渲染)

2.4 PTA提交列表说明。

刚开始没什么思路,想得有点复杂,还想着比较最小值什么的,后来一想修好的不是不用修吗,那不就是0,就豁然开朗了
2.1 题目2:7-7 旅游规划
2.2 设计思路(伪代码或流程图)
建图时多一个费用
然后初始化时对角线置为0
其他为极大值
然后用Floyd算法,就是判断时候多一个判断要费用最少的
for k=0 to n-1
for j=0 to n-1
for i=0 to n-1
{
if 长度更短或者长度一样但是花费少
更新之
}
2.3 代码截图(注意,截图、截图、截图。代码不要粘贴博客上。不用用···语法去渲染)

2.4 PTA提交列表说明。
这题还有一个测试点没有过,最大时运行超时,上课时炳辉同学介绍了用Dijkstra算法做,但是我就觉的Floyd算法代码量更少,就是不知道为什么运行超时
有空了再用Dijkstra算法做一下
3.截图本周题目集的PTA最后排名(3分)
本次题目集总分:310分
3.1 PTA排名(截图带自己名字的排名)

3.2 我的总分:251
- 阅读代码(必做,1分)
Bellman-Ford:
求单源最短路,可以判断有无负权回路(若有,则不存在最短路),
时效性较好,时间复杂度O(VE)。
#include <iostream>
#include <algorithm>
#include <cmath>
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <queue>
using namespace std;
int dis[10010];
int book[10010];
int origin[10010],destination[10010],value[10010];
int n,m;
int total;
int next[10010],head[10010];
void adl(int a,int b,int c)//邻接表
{
total++;
origin[total]=a;
destination[total]=b;
value[total]=c;
next[total]=head[a];
head[a]=total;
}
void Bellman_ford(int a)
{
memset(book,0,sizeof(book));//book[i]表示i号点是否在队列里
memset(dis,88,sizeof(dis));
queue <int> q;
q.push(a);
book[a]=1;
dis[a]=0;
while(!q.empty())//当队列不为空时更新
{
for(int e=head[q.front()];e;e=next[e])//枚举队首点相邻的每一个点
{
if(dis[destination[e]]>dis[origin[e]]+value[e])
{
dis[destination[e]]=dis[origin[e]]+value[e];
if(book[destination[e]]==0)
{
q.push(destination[e]);//将更新的这一个点入队
book[destination[e]]=1;
}
}
}
q.pop();//弹出队首元素
}
}
int main()
{
cin>>n>>m;
for(int i=1;i<=m;i++)
{
int a,b,c;
cin>>a>>b>>c;
adl(a,b,c);
}
Bellman_ford(1);
for(int i=1;i<=n;i++)
cout<<dis[i]<<" ";
}
该算法是利用动态规划的思想。该算法以自底向上的方式计算最短路径。
它首先计算最多一条边时的最短路径(对于所有顶点)。然后,计算最多两条边时的最短路径。
dijkstra固然很好用,但是却解决不了负权边,想要解决这个问题,就要用到Bellman-ford.



