NNDL 实验1

邱锡鹏，神经网络与深度学习，机械工业出版社，https://nndl.github.io/, 2020.

https://github.com/nndl/practice-in-paddle/

第1章实践基础

深度学习在很多领域中都有非常出色的表现，在图像识别、语音识别、自然语言处理、机器人、广告投放、医学诊断和金融等领域都有广泛应用。而目前深度学习的模型还主要是各种各样的神经网络。随着网络越来越复杂，从底层开始一步步实现深度学习系统变得非常低效，其中涉及模型搭建、梯度求解、并行计算、代码实现等多个环节。每一个环节都需要进行精心实现和检查，需要耗费开发人员很多的精力。为此，深度学习框架（也常称为机器学习框架）应运而生，它有助于研发人员聚焦任务和模型设计本身，省去大量而烦琐的代码编写工作，其优势主要表现在如下两个方面：

实现简单：深度学习框架屏蔽了底层实现，用户只需关注模型的逻辑结构，同时简化了计算逻辑，降低了深度学习入门门槛。
使用高效：深度学习框架具备灵活的移植性，在不同设备（CPU、GPU或移动端）之间无缝迁移，使得深度学习框架会使模型训练以及部署更高效。

本书使用飞桨框架作为实践的基础框架。飞桨（PaddlePaddle）框架是一套面向深度学习的基础训练和推理框架。飞桨于2016年正式开源，是主流深度学习开源框架中一款完全国产化的产品。目前，飞桨框架已经非常成熟并且易用，可以很好地支持本书的实践设计。

在讲解本书主要内容之前，本章先对实践环节的基础知识进行介绍，主要介绍以下内容：

张量（Tensor）：深度学习中表示和存储数据的主要形式。在动手实践机器学习之前，需要熟悉张量的概念、性质和运算规则，以及了解飞桨中张量的各种API。
算子（Operator）：构建神经网络模型的基础组件。每个算子有前向和反向计算过程，前向计算对应一个数学函数，而反向计算对应这个数学函数的梯度计算。有了算子，我们就可以很方便地通过算子来搭建复杂的神经网络模型，而不需要手工计算梯度。

此外，本章还汇总了在本书中自定义的一些算术、数据集以及轻量级训练框架Runner类。

1.1 如何运行本书的代码

笔记

本书涉及大量代码实践，通过运行代码理解如何构建模型及训练网络。本书中代码有两种运行方式：本地运行AI Studio运行。下面我们分别介绍两种运行方式的环境准备及操作方法。

1.1.1 本地运行

1.1.1.1 环境准备

本书代码基于Python语言与飞桨框架开发，如选择在本地运行请首先确认本机的操作系统、Python及pip版本是否满足飞桨支持的环境。目前飞桨支持的环境如下：

Linux 版本（64 bit）
- CentOS 7（GPU版本支持CUDA 10.1/10.2/11.0/11.1/11.2）
- Ubuntu 16.04（GPU版本支持CUDA 10.1/10.2/11.0/11.1/11.2）
- Ubuntu 18.04（GPU版本支持CUDA 10.1/10.2/11.0/11.1/11.2）
- Ubuntu 20.04（GPU版本支持CUDA 10.1/10.2/11.0/11.1/11.2）
Python版本3.6/3.7/3.8/3.9（64 bit）
pip或pip3版本20.2.2或更高版本（64 bit）

可以使用如下命令查看本机的操作系统和位数信息：

uname -m && cat /etc/*release

使用如下命令确认Python版本是否为3.6/3.7/3.8/3.9:

python --version

使用如下命令确认pip版本是否满足要求：

python -m ensurepip
python -m pip --version

确认Python和pip是64bit版本，且处理器架构是x86_64（或称作x64、Intel 64、AMD64）架构。需要注意，目前飞桨不支持arm64架构。

python -c "import platform;print(platform.architecture()[0]);print(platform.machine())"

该命令第一行输出为“64bit”，第二行输出为“x86_64”“x64”或“AMD64”即符合要求。

1.1.1.2 快速安装

本书第1章内容使用CPU即可完成，无须其他硬件设备。但从第2章开始，建议使用支持CUDA的GPU，书中代码默认在32G RAM的Tesla V100上运行，如使用其他配置的GPU可适当调整模型训练参数或直接通过AI Studio平台运行代码。

笔记
在GPU上运行模型训练代码可以大幅缩短模型训练时间，但使用GPU并不是必需的。如果电脑没有GPU硬件设备，本书内代码在仅使用CPU的情况下仍可以跑通，只是模型训练所需时间会增加。在这种情况下，可以使用AI Studio平台的免费GPU算力运行代码。使用方法详见第1.1.2节。

目前推荐使用飞桨开源框架v2.2版本，后续可在飞桨官网查看最新稳定版本。通过如下命令安装CPU版本：

python -m pip install paddlepaddle==2.2.2 -i https://mirror.baidu.com/pypi/simple

通过如下命令安装GPU版本：

python -m pip install paddlepaddle-gpu==2.2.2 -i https://mirror.baidu.com/pypi/simple

默认GPU环境为CUDA 10.2，如需安装基于其他CUDA版本的飞桨框架，可在2.2.2后面加入版本后缀，比如CUDA 10.1版本的飞桨框架对应为paddlepaddle-gpu==2.2.2.post101。

动手练习1.1

使用python命令进入python解释器，输入import paddle，验证安装是否成功。
输入paddle.__version__验证版本安装是否正确。
输入paddle.utils.run_check()，如出现“PaddlePaddle is installed successfully!”，则说明已正确安装。

1.1.2 AI Studio运行

AI Studio是基于飞桨的人工智能学习与实训社区，提供免费的算力支持，本书的内容在AI Studio上提供配套的BML Codelab项目。BML Codelab是面向个人和企业开发者的AI开发工具，基于Jupyter提供了在线的交互式开发环境。

BML Codelab目前默认使用飞桨2.2.2版本，无须额外安装。如图1.1所示，通过选择“启动环境”\(\rightarrow\)“基础版”即可在CPU环境下运行，选择“至尊版GPU”即可在32G RAM的Tesla V100上运行代码，至尊版GPU每天有8小时的免费使用时间。

图1.1 AI Studio项目运行环境选择

选择环境进入项目后，项目整体布局如图1.2所示。项目页面（Notebook）由侧边栏、菜单栏、快捷工具栏、状态监控栏和代码编辑区组成。这里我们重点介绍代码编辑区和快捷工具栏，其余边栏的使用方法可参见BML Codelab环境使用说明。

图1.2 BML Codelab项目布局

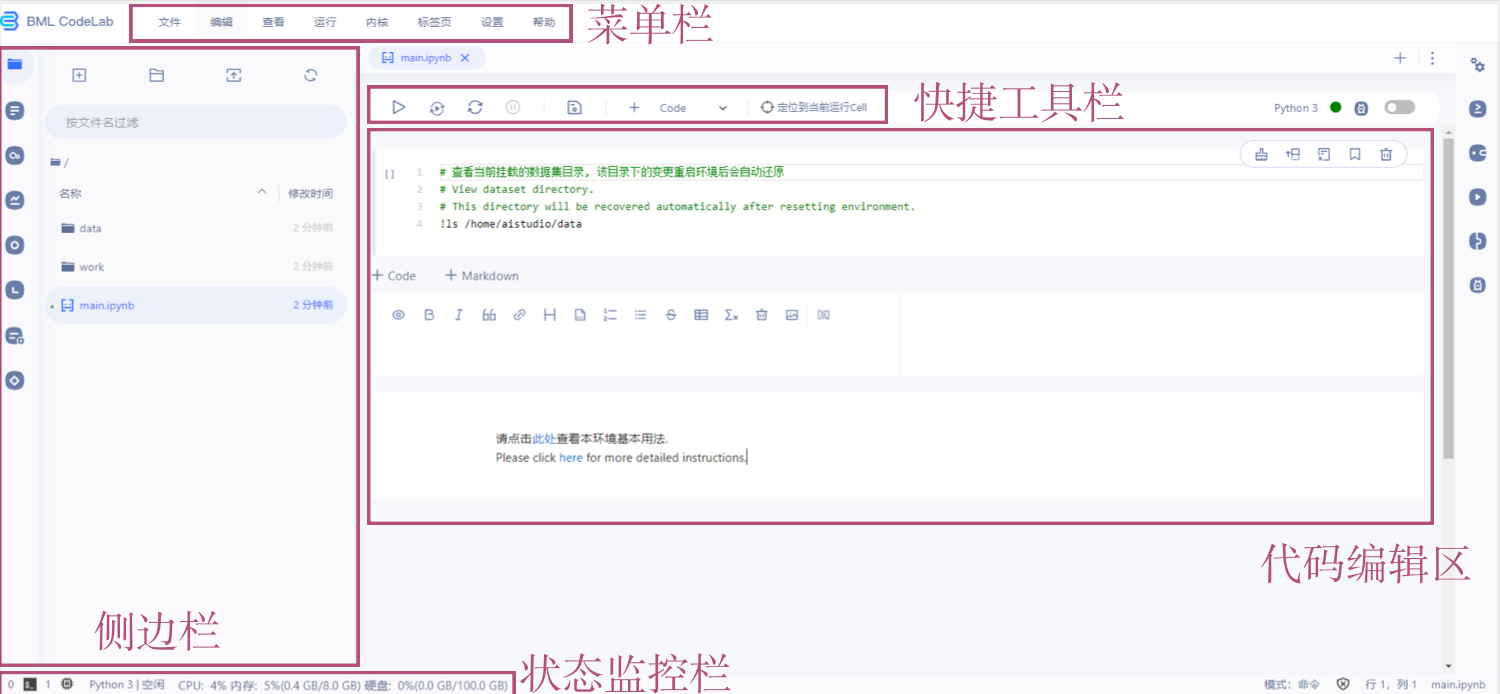
代码编辑区主要由代码编写单元(Code Cell)组成，在代码编写单元内编写Python代码或shell命令，点击“运行”按钮，代码或命令将在云端执行，并将结果返回到代码编写单元，直接显示在项目页面中。图1.3中我们简单定义两行代码，通过运行代码编写单元，得到输出结果。

图1.3 代码编写单元交互式运行

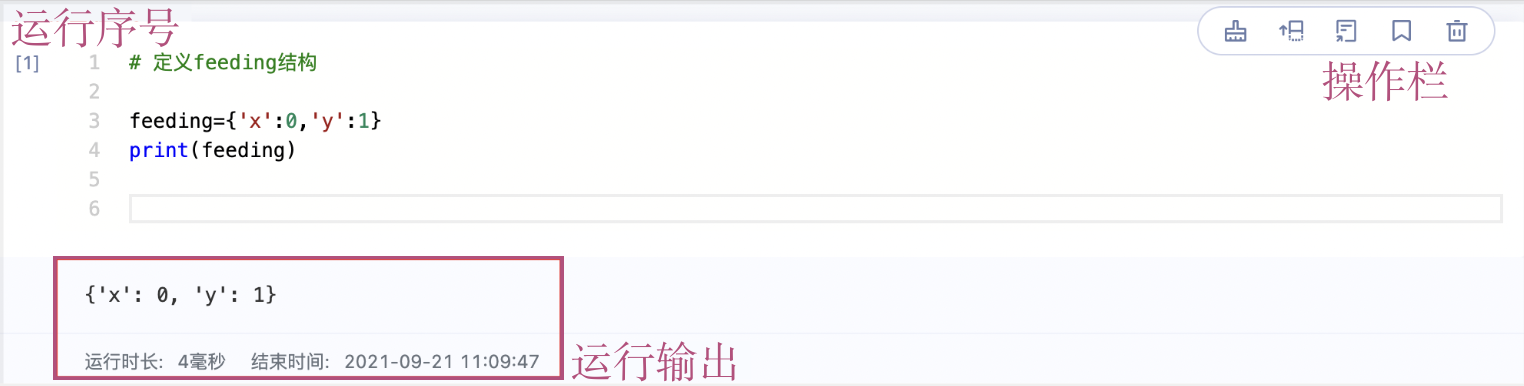
快捷工具栏内工具如图1.4所示，工具功能为：

运行：运行当前选中的代码编写单元。
停止运行：停止Notebook的运行状态。
重启内核：重启代码内核，清空环境中的环境变量、缓存变量、输出结果等.
保存：保存Notebook项目文件.
插入：添加指定类型的单元，支持Code和Markdown两种类型。
定位：定位到正在执行的单元。

图1.4 快捷工具栏

1.2 张量

在深度学习的实践中，我们通常使用向量或矩阵运算来提高计算效率。比如\(w_1x_1 + w_2 x_2 +\cdots +w_N x_N\)的计算可以用\(\bm w^\top \bm x\)来代替（其中\(\bm w=[w_1 w_2 \cdots w_N]^\top，\bm x=[x_1 x_2 \cdots x_N]^\top\)），这样可以充分利用计算机的并行计算能力，特别是利用GPU来实现高效矩阵运算。

在深度学习框架中，数据经常用张量(Tensor)的形式来存储。张量是矩阵的扩展与延伸，可以认为是高阶的矩阵。1阶张量为向量，2阶张量为矩阵。如果你对Numpy熟悉，那么张量是类似于Numpy的多维数组(ndarray)的概念，可以具有任意多的维度。

笔记

注意：这里的“维度”是“阶”的概念，和线性代数中向量的“维度”含义不同。

张量的大小可以用形状（shape）来描述。比如一个三维张量的形状是 \([2, 2, 5]\)，表示每一维（也称为轴（axis））的元素的数量，即第0轴上元素数量是2，第1轴上元素数量是2，第2轴上的元素数量为5。

图1.5给出了3种纬度的张量可视化表示。

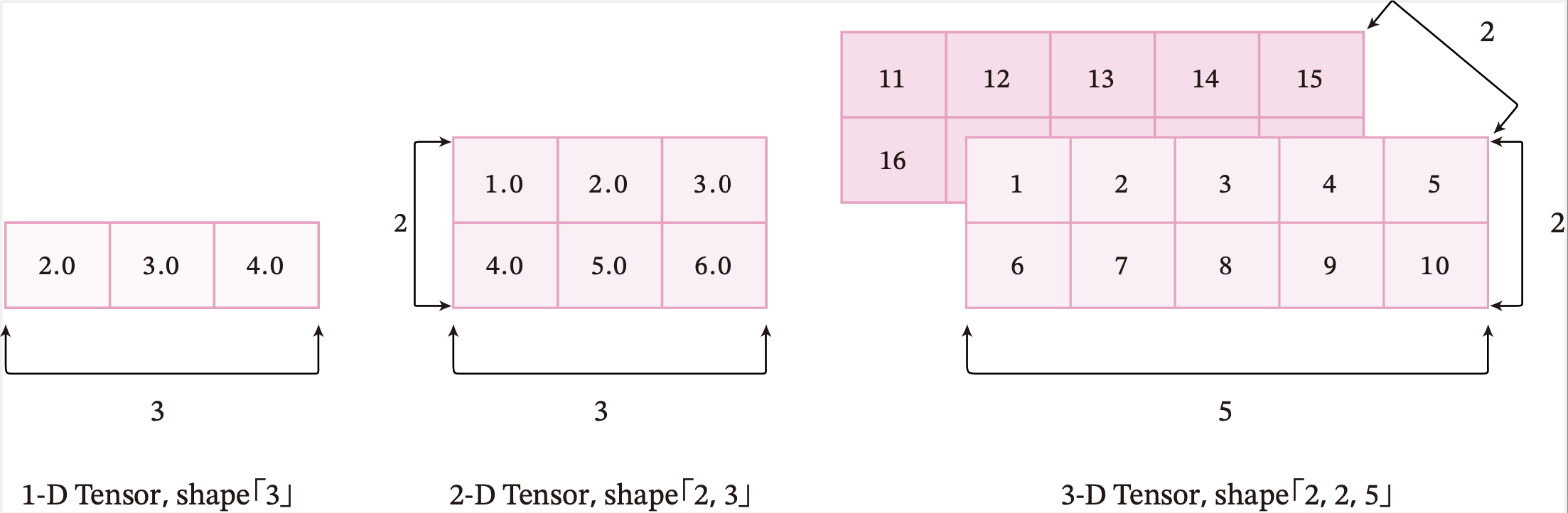
图1.5 不同维度的张量可视化表示

张量中元素的类型可以是布尔型数据、整数、浮点数或者复数，但同一张量中所有元素的数据类型均相同。因此我们可以给张量定义一个数据类型(dtype)来表示其元素的类型。

1.2.1 创建张量

创建一个张量可以有多种方式，如：指定数据创建、指定形状创建、指定区间创建等。

1.2.1.1 指定数据创建张量

通过给定Python列表数据，可以创建任意维度的张量。

（1）通过指定的Python列表数据[2.0, 3.0, 4.0]，创建一个一维张量。

# 导入PaddlePaddle
import paddle
# 创建一维Tensor
ndim_1_Tensor = paddle.to_tensor([2.0, 3.0, 4.0])
print(ndim_1_Tensor)

Tensor(shape=[3], dtype=float32, place=CPUPlace, stop_gradient=True,
       [2., 3., 4.])

（2）通过指定的Python列表数据来创建类似矩阵（matrix）的二维张量。

# 创建二维Tensor
ndim_2_Tensor = paddle.to_tensor([[1.0, 2.0, 3.0],
                                  [4.0, 5.0, 6.0]])
print(ndim_2_Tensor)

Tensor(shape=[2, 3], dtype=float32, place=CPUPlace, stop_gradient=True,
       [[1., 2., 3.],
        [4., 5., 6.]])

（3）同样地，还可以创建维度为3、4...N等更复杂的多维张量。

# 创建多维Tensor
ndim_3_Tensor = paddle.to_tensor([[[1, 2, 3, 4, 5],
                                   [6, 7, 8, 9, 10]],
                                  [[11, 12, 13, 14, 15],
                                   [16, 17, 18, 19, 20]]])
print(ndim_3_Tensor)

Tensor(shape=[2, 2, 5], dtype=int64, place=CPUPlace, stop_gradient=True,
       [[[1 , 2 , 3 , 4 , 5 ],
         [6 , 7 , 8 , 9 , 10]],

        [[11, 12, 13, 14, 15],
         [16, 17, 18, 19, 20]]])

需要注意的是，张量在任何一个维度上的元素数量必须相等。下面尝试定义一个在同一维度上元素数量不等的张量。

# 尝试定义在不同维度上元素数量不等的Tensor
ndim_2_Tensor = paddle.to_tensor([[1.0, 2.0],
                                  [4.0, 5.0, 6.0]])

输出结果为：

ValueError:
        Faild to convert input data to a regular ndarray :
         - Usually this means the input data contains nested lists with different lengths.

从输出结果看，这种定义情况会抛出异常，提示在任何维度上的元素数量必须相等。

1.2.1.2 指定形状创建

如果要创建一个指定形状、元素数据相同的张量，可以使用paddle.zeros、paddle.ones、paddle.full等API。

m, n = 2, 3

# 使用paddle.zeros创建数据全为0，形状为[m, n]的Tensor
zeros_Tensor = paddle.zeros([m, n])

# 使用paddle.ones创建数据全为1，形状为[m, n]的Tensor
ones_Tensor = paddle.ones([m, n])

# 使用paddle.full创建数据全为指定值，形状为[m, n]的Tensor，这里我们指定数据为10
full_Tensor = paddle.full([m, n], 10)

print('zeros Tensor: ', zeros_Tensor)
print('ones Tensor: ', ones_Tensor)
print('full Tensor: ', full_Tensor)

zeros Tensor:  Tensor(shape=[2, 3], dtype=float32, place=CPUPlace, stop_gradient=True,
       [[0., 0., 0.],
        [0., 0., 0.]])
ones Tensor:  Tensor(shape=[2, 3], dtype=float32, place=CPUPlace, stop_gradient=True,
       [[1., 1., 1.],
        [1., 1., 1.]])
full Tensor:  Tensor(shape=[2, 3], dtype=float32, place=CPUPlace, stop_gradient=True,
       [[10., 10., 10.],
        [10., 10., 10.]])

1.2.1.3 指定区间创建

如果要在指定区间内创建张量，可以使用paddle.arange、paddle.linspace等API。

# 使用paddle.arange创建以步长step均匀分隔数值区间[start, end)的一维Tensor
arange_Tensor = paddle.arange(start=1, end=5, step=1)

# 使用paddle.linspace创建以元素个数num均匀分隔数值区间[start, stop]的Tensor
linspace_Tensor = paddle.linspace(start=1, stop=5, num=5)

print('arange Tensor: ', arange_Tensor)
print('linspace Tensor: ', linspace_Tensor)

arange Tensor:  Tensor(shape=[4], dtype=int64, place=CPUPlace, stop_gradient=True,
       [1, 2, 3, 4])
linspace Tensor:  Tensor(shape=[5], dtype=float32, place=CPUPlace, stop_gradient=True,
       [1., 2., 3., 4., 5.])

1.2.2 张量的属性

1.2.2.1 张量的形状

张量具有如下形状属性：

Tensor.ndim：张量的维度，例如向量的维度为1，矩阵的维度为2。
Tensor.shape：张量每个维度上元素的数量。
Tensor.shape[n]：张量第\(n\)维的大小。第\(n\)维也称为轴（axis）。
Tensor.size：张量中全部元素的个数。

为了更好地理解ndim、shape、axis、size四种属性间的区别，创建一个如图1.6所示的四维张量。

图1.6 形状为[2, 3, 4, 5]的四维张量

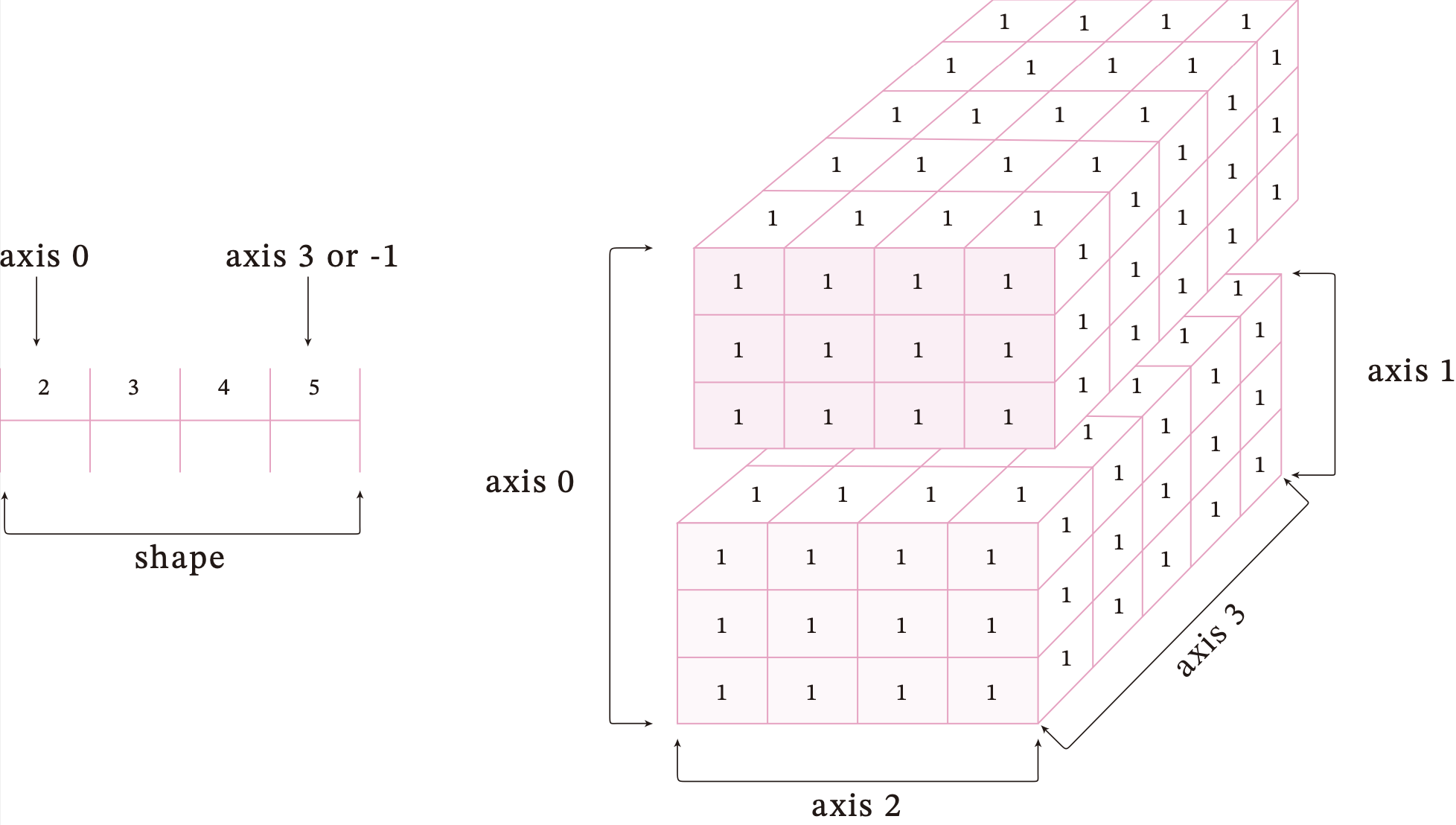
创建一个四维张量，并打印出shape、ndim、shape[n]、size属性。

ndim_4_Tensor = paddle.ones([2, 3, 4, 5])

print("Number of dimensions:", ndim_4_Tensor.ndim)
print("Shape of Tensor:", ndim_4_Tensor.shape)
print("Elements number along axis 0 of Tensor:", ndim_4_Tensor.shape[0])
print("Elements number along the last axis of Tensor:", ndim_4_Tensor.shape[-1])
print('Number of elements in Tensor: ', ndim_4_Tensor.size)

Number of dimensions: 4
Shape of Tensor: [2, 3, 4, 5]
Elements number along axis 0 of Tensor: 2
Elements number along the last axis of Tensor: 5
Number of elements in Tensor:  120

1.2.2.2 形状的改变

除了查看张量的形状外，重新设置张量的在实际编程中也具有重要意义，飞桨提供了paddle.reshape接口来改变张量的形状。

# 定义一个shape为[3,2,5]的三维Tensor
ndim_3_Tensor = paddle.to_tensor([[[1, 2, 3, 4, 5],
                                   [6, 7, 8, 9, 10]],
                                  [[11, 12, 13, 14, 15],
                                   [16, 17, 18, 19, 20]],
                                  [[21, 22, 23, 24, 25],
                                   [26, 27, 28, 29, 30]]])
print("the shape of ndim_3_Tensor:", ndim_3_Tensor.shape)

# paddle.reshape 可以保持在输入数据不变的情况下，改变数据形状。这里我们设置reshape为[2,5,3]
reshape_Tensor = paddle.reshape(ndim_3_Tensor, [2, 5, 3])
print("After reshape:", reshape_Tensor)

the shape of ndim_3_Tensor: [3, 2, 5]
After reshape: Tensor(shape=[2, 5, 3], dtype=int64, place=CPUPlace, stop_gradient=True,
       [[[1 , 2 , 3 ],
         [4 , 5 , 6 ],
         [7 , 8 , 9 ],
         [10, 11, 12],
         [13, 14, 15]],

        [[16, 17, 18],
         [19, 20, 21],
         [22, 23, 24],
         [25, 26, 27],
         [28, 29, 30]]])

从输出结果看，将张量从[3, 2, 5]的形状reshape为[2, 5, 3]的形状时，张量内的数据不会发生改变，元素顺序也没有发生改变，只有数据形状发生了改变。

笔记

使用reshape时存在一些技巧，比如：

-1表示这个维度的值是从张量的元素总数和剩余维度推断出来的。因此，有且只有一个维度可以被设置为-1。
0表示实际的维数是从张量的对应维数中复制出来的，因此shape中0所对应的索引值不能超过张量的总维度。

分别对上文定义的ndim_3_Tensor进行reshape为[-1]和reshape为[0, 5, 2]两种操作，观察新张量的形状。

new_Tensor1 = ndim_3_Tensor.reshape([-1])
print('new Tensor 1 shape: ', new_Tensor1.shape)
new_Tensor2 = ndim_3_Tensor.reshape([0, 5, 2])
print('new Tensor 2 shape: ', new_Tensor2.shape)

new Tensor 1 shape:  [30]
new Tensor 2 shape:  [3, 5, 2]

从输出结果看，第一行代码中的第一个reshape操作将张量reshape为元素数量为30的一维向量；第四行代码中的第二个reshape操作中，0对应的维度的元素个数与原张量在该维度上的元素个数相同。

除使用paddle.reshape进行张量形状的改变外，还可以通过paddle.unsqueeze将张量中的一个或多个维度中插入尺寸为1的维度。

ones_Tensor = paddle.ones([5, 10])
new_Tensor1 = paddle.unsqueeze(ones_Tensor, axis=0)
print('new Tensor 1 shape: ', new_Tensor1.shape)
new_Tensor2 = paddle.unsqueeze(ones_Tensor, axis=[1, 2])
print('new Tensor 2 shape: ', new_Tensor2.shape)

new Tensor 1 shape:  [1, 5, 10]
new Tensor 2 shape:  [5, 1, 1, 10]

1.2.2.3 张量的数据类型

飞桨中可以通过Tensor.dtype来查看张量的数据类型，类型支持bool、float16、float32、float64、uint8、int8、int16、int32、int64和复数类型数据。

1）通过Python元素创建的张量，可以通过dtype来指定数据类型，如果未指定：

对于Python整型数据，则会创建int64型张量。
对于Python浮点型数据，默认会创建float32型张量。

2）通过Numpy数组创建的张量，则与其原来的数据类型保持相同。通过paddle.to_tensor()函数可以将Numpy数组转化为张量。

# 使用paddle.to_tensor通过已知数据来创建一个Tensor
print("Tensor dtype from Python integers:", paddle.to_tensor(1).dtype)
print("Tensor dtype from Python floating point:", paddle.to_tensor(1.0).dtype)

Tensor dtype from Python integers: paddle.int64
Tensor dtype from Python floating point: paddle.float32

如果想改变张量的数据类型，可以通过调用paddle.castAPI来实现。

# 定义dtype为float32的Tensor
float32_Tensor = paddle.to_tensor(1.0)
# paddle.cast可以将输入数据的数据类型转换为指定的dtype并输出。支持输出和输入数据类型相同。
int64_Tensor = paddle.cast(float32_Tensor, dtype='int64')
print("Tensor after cast to int64:", int64_Tensor.dtype)

Tensor after cast to int64: paddle.int64

1.2.2.4 张量的设备位置

初始化张量时可以通过place来指定其分配的设备位置，可支持的设备位置有三种：CPU、GPU和固定内存。

固定内存也称为不可分页内存或锁页内存，它与GPU之间具有更高的读写效率，并且支持异步传输，这对网络整体性能会有进一步提升，但它的缺点是分配空间过多时可能会降低主机系统的性能，因为它减少了用于存储虚拟内存数据的可分页内存。当未指定设备位置时，张量默认设备位置和安装的飞桨版本一致，如安装了GPU版本的飞桨，则设备位置默认为GPU。

如下代码分别创建了CPU、GPU和固定内存上的张量，并通过Tensor.place查看张量所在的设备位置。

# 创建CPU上的Tensor
cpu_Tensor = paddle.to_tensor(1, place=paddle.CPUPlace())
# 通过Tensor.place查看张量所在设备位置
print('cpu Tensor: ', cpu_Tensor.place)
# 创建GPU上的Tensor
gpu_Tensor = paddle.to_tensor(1, place=paddle.CUDAPlace(0))
print('gpu Tensor: ', gpu_Tensor.place)
# 创建固定内存上的Tensor
pin_memory_Tensor = paddle.to_tensor(1, place=paddle.CUDAPinnedPlace())
print('pin memory Tensor: ', pin_memory_Tensor.place)

输出结果为：

cpu Tensor:  CPUPlace
gpu Tensor:  CUDAPlace(0)
pin memory Tensor:  CUDAPinnedPlace

1.2.3 张量与Numpy数组转换

张量和Numpy数组可以相互转换。第1.2.2.3节中我们了解到paddle.to_tensor()函数可以将Numpy数组转化为张量，也可以通过Tensor.numpy()函数将张量转化为Numpy数组。

ndim_1_Tensor = paddle.to_tensor([1., 2.])
# 将当前 Tensor 转化为 numpy.ndarray
print('Tensor to convert: ', ndim_1_Tensor.numpy())

Tensor to convert:  [1. 2.]

1.2.4 张量的访问

1.2.4.1 索引和切片

我们可以通过索引或切片方便地访问或修改张量。飞桨使用标准的Python索引规则与Numpy索引规则，具有以下特点：

基于\(0-n\)的下标进行索引，如果下标为负数，则从尾部开始计算。
通过冒号“:”分隔切片参数start:stop:step来进行切片操作，也就是访问start到stop范围内的部分元素并生成一个新的序列。其中start为切片的起始位置，stop为切片的截止位置，step是切片的步长，这三个参数均可缺省。

1.2.4.2 访问张量

针对一维张量，对单个轴进行索引和切片。

# 定义1个一维Tensor
ndim_1_Tensor = paddle.to_tensor([0, 1, 2, 3, 4, 5, 6, 7, 8])

print("Origin Tensor:", ndim_1_Tensor)
print("First element:", ndim_1_Tensor[0])
print("Last element:", ndim_1_Tensor[-1])
print("All element:", ndim_1_Tensor[:])
print("Before 3:", ndim_1_Tensor[:3])
print("Interval of 3:", ndim_1_Tensor[::3])
print("Reverse:", ndim_1_Tensor[::-1])

Origin Tensor: Tensor(shape=[9], dtype=int64, place=CPUPlace, stop_gradient=True,
       [0, 1, 2, 3, 4, 5, 6, 7, 8])
First element: Tensor(shape=[1], dtype=int64, place=CPUPlace, stop_gradient=True,
       [0])
Last element: Tensor(shape=[1], dtype=int64, place=CPUPlace, stop_gradient=True,
       [8])
All element: Tensor(shape=[9], dtype=int64, place=CPUPlace, stop_gradient=True,
       [0, 1, 2, 3, 4, 5, 6, 7, 8])
Before 3: Tensor(shape=[3], dtype=int64, place=CPUPlace, stop_gradient=True,
       [0, 1, 2])
Interval of 3: Tensor(shape=[3], dtype=int64, place=CPUPlace, stop_gradient=True,
       [0, 3, 6])
Reverse: Tensor(shape=[9], dtype=int64, place=CPUPlace, stop_gradient=True,
       [8, 7, 6, 5, 4, 3, 2, 1, 0])

针对二维及以上维度的张量，在多个维度上进行索引或切片。索引或切片的第一个值对应第0维，第二个值对应第1维，以此类推，如果某个维度上未指定索引，则默认为“:”。

# 定义1个二维Tensor
ndim_2_Tensor = paddle.to_tensor([[0, 1, 2, 3],
                                  [4, 5, 6, 7],
                                  [8, 9, 10, 11]])
print("Origin Tensor:", ndim_2_Tensor)
print("First row:", ndim_2_Tensor[0])
print("First row:", ndim_2_Tensor[0, :])
print("First column:", ndim_2_Tensor[:, 0])
print("Last column:", ndim_2_Tensor[:, -1])
print("All element:", ndim_2_Tensor[:])
print("First row and second column:", ndim_2_Tensor[0, 1])

Origin Tensor: Tensor(shape=[3, 4], dtype=int64, place=CPUPlace, stop_gradient=True,
       [[0 , 1 , 2 , 3 ],
        [4 , 5 , 6 , 7 ],
        [8 , 9 , 10, 11]])
First row: Tensor(shape=[4], dtype=int64, place=CPUPlace, stop_gradient=True,
       [0, 1, 2, 3])
First row: Tensor(shape=[4], dtype=int64, place=CPUPlace, stop_gradient=True,
       [0, 1, 2, 3])
First column: Tensor(shape=[3], dtype=int64, place=CPUPlace, stop_gradient=True,
       [0, 4, 8])
Last column: Tensor(shape=[3], dtype=int64, place=CPUPlace, stop_gradient=True,
       [3 , 7 , 11])
All element: Tensor(shape=[3, 4], dtype=int64, place=CPUPlace, stop_gradient=True,
       [[0 , 1 , 2 , 3 ],
        [4 , 5 , 6 , 7 ],
        [8 , 9 , 10, 11]])
First row and second column: Tensor(shape=[1], dtype=int64, place=CPUPlace, stop_gradient=True,
       [1])

1.2.4.3 修改张量

与访问张量类似，可以在单个或多个轴上通过索引或切片操作来修改张量。

提醒
慎重通过索引或切片操作来修改张量，此操作仅会原地修改该张量的数值，且原值不会被保存。如果被修改的张量参与梯度计算，将仅会使用修改后的数值，这可能会给梯度计算引入风险。

# 定义1个二维Tensor
ndim_2_Tensor = paddle.ones([2, 3], dtype='float32')
print('Origin Tensor: ', ndim_2_Tensor)
# 修改第1维为0
ndim_2_Tensor[0] = 0
print('change Tensor: ', ndim_2_Tensor)
# 修改第1维为2.1
ndim_2_Tensor[0:1] = 2.1
print('change Tensor: ', ndim_2_Tensor)
# 修改全部Tensor
ndim_2_Tensor[...] = 3
print('change Tensor: ', ndim_2_Tensor)

Origin Tensor:  Tensor(shape=[2, 3], dtype=float32, place=CPUPlace, stop_gradient=True,
       [[1., 1., 1.],
        [1., 1., 1.]])
change Tensor:  Tensor(shape=[2, 3], dtype=float32, place=CPUPlace, stop_gradient=True,
       [[0., 0., 0.],
        [1., 1., 1.]])
change Tensor:  Tensor(shape=[2, 3], dtype=float32, place=CPUPlace, stop_gradient=True,
       [[2.09999990, 2.09999990, 2.09999990],
        [1.        , 1.        , 1.        ]])
change Tensor:  Tensor(shape=[2, 3], dtype=float32, place=CPUPlace, stop_gradient=True,
       [[3., 3., 3.],
        [3., 3., 3.]])

1.2.5 张量的运算

张量支持包括基础数学运算、逻辑运算、矩阵运算等100余种运算操作，以加法为例，有如下两种实现方式：
1）使用飞桨API paddle.add(x,y)。
2）使用张量类成员函数x.add(y)。

# 定义两个Tensor
x = paddle.to_tensor([[1.1, 2.2], [3.3, 4.4]], dtype="float64")
y = paddle.to_tensor([[5.5, 6.6], [7.7, 8.8]], dtype="float64")
# 第一种调用方法，paddle.add逐元素相加算子，并将各个位置的输出元素保存到返回结果中
print('Method 1: ', paddle.add(x, y))
# 第二种调用方法
print('Method 2: ', x.add(y))

Method 1:  Tensor(shape=[2, 2], dtype=float64, place=CPUPlace, stop_gradient=True,
       [[6.60000000 , 8.80000000 ],
        [11.        , 13.20000000]])
Method 2:  Tensor(shape=[2, 2], dtype=float64, place=CPUPlace, stop_gradient=True,
       [[6.60000000 , 8.80000000 ],
        [11.        , 13.20000000]])

从输出结果看，使用张量类成员函数和飞桨API具有相同的效果。

笔记
由于张量类成员函数操作更为方便，以下均从张量类成员函数的角度，对常用张量操作进行介绍。

笔记
更多张量操作相关的API，请参考飞桨官方文档。

1.2.5.1 数学运算

张量类的基础数学函数如下：

x.abs()                       # 逐元素取绝对值
x.ceil()                      # 逐元素向上取整
x.floor()                     # 逐元素向下取整
x.round()                     # 逐元素四舍五入
x.exp()                       # 逐元素计算自然常数为底的指数
x.log()                       # 逐元素计算x的自然对数
x.reciprocal()                # 逐元素求倒数
x.square()                    # 逐元素计算平方
x.sqrt()                      # 逐元素计算平方根
x.sin()                       # 逐元素计算正弦
x.cos()                       # 逐元素计算余弦
x.add(y)                      # 逐元素加
x.subtract(y)                 # 逐元素减
x.multiply(y)                 # 逐元素乘（积）
x.divide(y)                   # 逐元素除
x.mod(y)                      # 逐元素除并取余
x.pow(y)                      # 逐元素幂
x.max()                       # 指定维度上元素最大值，默认为全部维度
x.min()                       # 指定维度上元素最小值，默认为全部维度
x.prod()                      # 指定维度上元素累乘，默认为全部维度
x.sum()                       # 指定维度上元素的和，默认为全部维度

同时，为了更方便地使用张量，飞桨对Python数学运算相关的魔法函数进行了重写，以下操作与上述结果相同。

x + y  -> x.add(y)            # 逐元素加
x - y  -> x.subtract(y)       # 逐元素减
x * y  -> x.multiply(y)       # 逐元素乘（积）
x / y  -> x.divide(y)         # 逐元素除
x % y  -> x.mod(y)            # 逐元素除并取余
x ** y -> x.pow(y)            # 逐元素幂

1.2.5.2 逻辑运算

张量类的逻辑运算函数如下：

x.isfinite()                  # 判断Tensor中元素是否是有限的数字，即不包括inf与nan
x.equal_all(y)                # 判断两个Tensor的全部元素是否相等，并返回形状为[1]的布尔类Tensor
x.equal(y)                    # 判断两个Tensor的每个元素是否相等，并返回形状相同的布尔类Tensor
x.not_equal(y)                # 判断两个Tensor的每个元素是否不相等
x.less_than(y)                # 判断Tensor x的元素是否小于Tensor y的对应元素
x.less_equal(y)               # 判断Tensor x的元素是否小于或等于Tensor y的对应元素
x.greater_than(y)             # 判断Tensor x的元素是否大于Tensor y的对应元素
x.greater_equal(y)            # 判断Tensor x的元素是否大于或等于Tensor y的对应元素
x.allclose(y)                 # 判断两个Tensor的全部元素是否接近

同样地，飞桨对Python逻辑比较相关的魔法函数也进行了重写，这里不再赘述。

1.2.5.3 矩阵运算

张量类还包含了矩阵运算相关的函数，如矩阵的转置、范数计算和乘法等。

x.t()                         # 矩阵转置
x.transpose([1, 0])           # 交换第 0 维与第 1 维的顺序
x.norm('fro')                 # 矩阵的弗罗贝尼乌斯范数
x.dist(y, p=2)                # 矩阵（x-y）的2范数
x.matmul(y)                   # 矩阵乘法

有些矩阵运算中也支持大于两维的张量，比如matmul函数，对最后两个维度进行矩阵乘。比如x是形状为[j,k,n,m]的张量，另一个y是[j,k,m,p]的张量，则x.matmul(y)输出的张量形状为[j,k,n,p]。

1.2.5.4 广播机制

飞桨的一些API在计算时支持广播(Broadcasting)机制，允许在一些运算时使用不同形状的张量。通常来讲，如果有一个形状较小和一个形状较大的张量，会希望多次使用较小的张量来对较大的张量执行某些操作，看起来像是形状较小的张量首先被扩展到和较大的张量形状一致，然后再做运算。

广播机制的条件

飞桨的广播机制主要遵循如下规则（参考Numpy广播机制）：

1）每个张量至少为一维张量。

2）从后往前比较张量的形状，当前维度的大小要么相等，要么其中一个等于1，要么其中一个不存在。

# 当两个Tensor的形状一致时，可以广播
x = paddle.ones((2, 3, 4))
y = paddle.ones((2, 3, 4))
z = x + y
print('broadcasting with two same shape tensor: ', z.shape)

x = paddle.ones((2, 3, 1, 5))
y = paddle.ones((3, 4, 1))
# 从后往前依次比较：
# 第一次：y的维度大小是1
# 第二次：x的维度大小是1
# 第三次：x和y的维度大小相等，都为3
# 第四次：y的维度不存在
# 所以x和y是可以广播的
z = x + y
print('broadcasting with two different shape tensor:', z.shape)

broadcasting with two same shape tensor:  [2, 3, 4]
broadcasting with two different shape tensor: [2, 3, 4, 5]

从输出结果看，x与y在上述两种情况中均遵循广播规则，因此在张量相加时可以广播。我们再定义两个shape分别为[2, 3, 4]和[2, 3, 6]的张量，观察这两个张量是否能够通过广播操作相加。

x = paddle.ones((2, 3, 4))
y = paddle.ones((2, 3, 6))
z = x + y

输出结果为：

ValueError: (InvalidArgument) Broadcast dimension mismatch.

从输出结果看，此时x和y是不能广播的，因为在第一次从后往前的比较中，4和6不相等，不符合广播规则。

广播机制的计算规则

现在我们知道在什么情况下两个张量是可以广播的。两个张量进行广播后的结果张量的形状计算规则如下：

1）如果两个张量shape的长度不一致，那么需要在较小长度的shape前添加1，直到两个张量的形状长度相等。

2）保证两个张量形状相等之后，每个维度上的结果维度就是当前维度上较大的那个。

以张量x和y进行广播为例，x的shape为[2, 3, 1，5]，张量y的shape为[3，4，1]。首先张量y的形状长度较小，因此要将该张量形状补齐为[1, 3, 4, 1]，再对两个张量的每一维进行比较。从第一维看，x在一维上的大小为2，y为1，因此，结果张量在第一维的大小为2。以此类推，对每一维进行比较，得到结果张量的形状为[2, 3, 4, 5]。

由于矩阵乘法函数paddle.matmul在深度学习中使用非常多，这里需要特别说明一下它的广播规则：

1）如果两个张量均为一维，则获得点积结果。

2）如果两个张量都是二维的，则获得矩阵与矩阵的乘积。

3）如果张量x是一维，y是二维，则将x的shape转换为[1, D]，与y进行矩阵相乘后再删除前置尺寸。

4）如果张量x是二维，y是一维，则获得矩阵与向量的乘积。

5）如果两个张量都是N维张量（N > 2），则根据广播规则广播非矩阵维度（除最后两个维度外其余维度）。比如：如果输入x是形状为[j,1,n,m]的张量，另一个y是[k,m,p]的张量，则输出张量的形状为[j,k,n,p]。

x = paddle.ones([10, 1, 5, 2])
y = paddle.ones([3, 2, 5])
z = paddle.matmul(x, y)
print('After matmul: ', z.shape)

After matmul:  [10, 3, 5, 5]

从输出结果看，计算张量乘积时会使用到广播机制。

笔记
飞桨的API有原位（inplace）操作和非原位操作之分。原位操作即在原张量上保存操作结果，非原位操作则不会修改原张量，而是返回一个新的张量来表示运算结果。在飞桨框架V2.1及之后版本，部分API有对应的原位操作版本，在API后加上'_'表示，如：x.add(y)是非原位操作，x.add_(y)为原位操作。

动手练习1.2
尝试和熟悉本节中的各种张量运算，特别是掌握张量计算时的广播机制。

1.3 算子

一个复杂的机器学习模型（比如神经网络）可以看作一个复合函数，输入是数据特征，输出是标签的值或概率。简单起见，假设一个由\(L\)个函数复合的神经网络定义为：

\[y=f_L(\cdots f_2(f_1(x))), \]

其中\(f_l(\cdot)\)可以为带参数的函数，也可以为不带参数的函数，\(x\)为输入特征，\(y\)为某种损失。
我们将从\(x\)到\(y\)的计算看作一个前向计算过程。而神经网络的参数学习需要计算损失关于所有参数的偏导数（即梯度）。假设函数\(f_l(\cdot)\)包含参数\(\theta_l\)，根据链式法则，

\[\begin{aligned} \frac{\partial y}{\partial \theta_l} &= {\frac{\partial f_l}{\partial \theta_l}} \frac{\partial y}{\partial f_l} \\ &= \frac{\partial f_l}{\partial \theta_l} \frac{\partial f_{l+1}}{\partial f_l} \cdots \frac{\partial f_L}{\partial f_{L-1}} . \end{aligned} \]

在实践中，一种比较高效的计算\(y\)关于每个函数\(f_l\)的偏导数的方式是利用递归进行反向计算。令\(\delta_l\triangleq \frac{\partial y}{\partial f_l}\)，则有

\[\delta_{l-1} = \frac{\partial f_l}{\partial f_{l-1}} \delta_{l}. \]

如果将函数\(f_l(\cdot)\)称为前向函数，则\(\delta_{l-1}\)的计算称为函数\(f(x)\)的反向函数。

如果我们实现每个基础函数的前向函数和反向函数，就可以非常方便地通过这些基础函数组合出复杂函数，并通过链式法则反向计算复杂函数的偏导数。
在深度学习框架中，这些基本函数的实现称为算子(Operator，Op)。有了算子，就可以像搭积木一样构建复杂的模型。

1.3.1 算子定义

算子是构建复杂机器学习模型的基础组件，包含一个函数\(f(x)\)的前向函数和反向函数。为了可以更便捷地进行算子组合，本书中定义算子Op}的接口如下：

class Op(object):
    def __init__(self):
        pass

    def __call__(self, inputs):
        return self.forward(inputs)

    # 前向函数
    # 输入：张量inputs
    # 输出：张量outputs
    def forward(self, inputs):
        # return outputs
        raise NotImplementedError

    # 反向函数
    # 输入：最终输出对outputs的梯度outputs_grads
    # 输出：最终输出对inputs的梯度inputs_grads
    def backward(self, outputs_grads):
        # return inputs_grads
        raise NotImplementedError

在上面的接口中，forward是自定义Op的前向函数，必须被子类重写，它的参数为输入对象，参数的类型和数量任意；backward是自定义Op的反向函数，必须被子类重写，它的参数为forward输出张量的梯度outputs_grads，它的输出为forward输入张量的梯度inputs_grads。

笔记
在飞桨中，可以直接调用模型的forward()方法进行前向执行，也可以调用__call__，从而执行在forward()中定义的前向计算逻辑。

下面以\(g = \exp(a \times b+c \times d)\)为例，分别实现加法、乘法和指数运算三个算子，通过算子组合计算\(y\)值。

1.3.1.1 加法算子

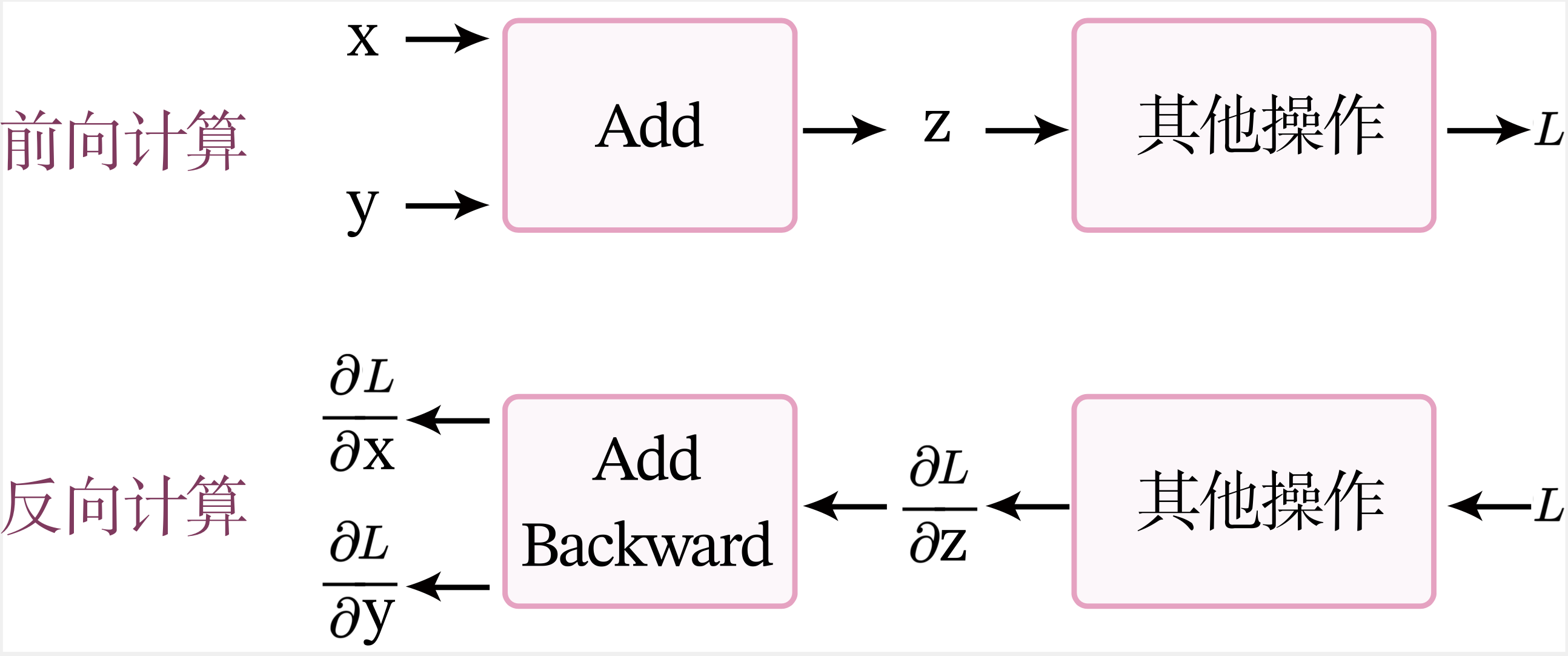
图1.7展示了加法算子的前反向计算过程。

图1.7 加法算子的前反向函数

前向计算

当进行前向计算时，加法计算输出\(z=x+y\)。

反向计算

假设经过一个其他操作后，最终输出为\(L\)，令\(\delta_z=\frac{\partial L}{\partial z}\)，\(\delta_x=\frac{\partial L}{\partial x}\)，\(\delta_y=\frac{\partial L}{\partial y}\)。
加法算子的反向计算的输入是梯度\(\delta_z\)，输出是梯度\(\delta_x\)和\(\delta_y\)。

根据链式法则，\(\delta_x = \delta_z \times 1\)，\(\delta_y = \delta_z \times 1\)。
加法算子的代码实现如下：

class add(Op):
    def __init__(self):
        super(add, self).__init__()

    def __call__(self, x, y):
        return self.forward(x, y)

    def forward(self, x, y):
        self.x = x
        self.y = y
        outputs = x + y
        return outputs

    def backward(self, grads):
        grads_x = grads * 1
        grads_y = grads * 1
        return grads_x, grads_y

定义\(x=1\)、\(y=4\)，根据反向计算，得到\(x\)、\(y\)的梯度。

x = 1
y = 4
add_op = add()
z = add_op(x, y)
grads_x, grads_y = add_op.backward(grads=1)
print("x's grad is: ", grads_x)
print("y's grad is: ", grads_y)

x's grad is:  1
y's grad is:  1

1.3.1.2 乘法算子

同理，乘法算子的代码实现如下：

class multiply(Op):
    def __init__(self):
        super(multiply, self).__init__()

    def __call__(self, x, y):
        return self.forward(x, y)

    def forward(self, x, y):
        self.x = x
        self.y = y
        outputs = x * y
        return outputs

    def backward(self, grads):
        grads_x = grads * self.y
        grads_y = grads * self.x
        return grads_x, grads_y

1.3.1.3 指数算子

同理，指数算子的代码实现如下：

import math

class exponential(Op):
    def __init__(self):
        super(exponential, self).__init__()

    def forward(self, x):
        self.x = x
        outputs = math.exp(x)
        return outputs

    def backward(self, grads):
        grads = grads * math.exp(self.x)
        return grads

分别指定\(a、b、c、d\)的值，通过实例化算子，调用加法、乘法和指数运算算子，计算得到\(y\)。

a, b, c, d = 2, 3, 2, 2
# 实例化算子
multiply_op = multiply()
add_op = add()
exp_op = exponential()
y = exp_op(add_op(multiply_op(a, b), multiply_op(c, d)))
print('y: ', y)

y:  22026.465794806718

动手练习1.3

执行上述算子的反向过程，并验证梯度是否正确。

1.3.2 自动微分机制

目前大部分深度学习平台都支持自动微分（Automatic Differentiation），即根据forward()函数来自动构建backward()函数。

笔记

自动微分的原理是将所有的数值计算都分解为基本的原子操作，并构建\mykey{计算图}{Computational Graph}。计算图上每个节点都是一个原子操作，保留前向和反向的计算结果，很方便通过链式法则来计算梯度。自动微分的详细介绍可以参考《神经网络与深度学习》第4.5节。

飞桨的自动微分是通过trace的方式，记录各种算子和张量的前向计算，并自动创建相应的反向函数和反向变量，来实现反向梯度的计算。

笔记

在飞桨中，可以通过paddle.grad()API或张量类成员函数x.grad来查看张量的梯度。

下面用一个比较简单的例子来了解整个过程。定义两个张量a和b，并用stop_gradient属性用来设置是否传递梯度。将a的stop_gradient属性设为False，会自动为a创建一个反向张量，将b的stop_gradient属性设为True，即不会为b创建反向张量。

# 定义张量a，stop_gradient=False代表进行梯度传导
a = paddle.to_tensor(2.0, stop_gradient=False)
# 定义张量b，stop_gradient=True代表不进行梯度传导
b = paddle.to_tensor(5.0, stop_gradient=True)
c = a * b
# 自动计算反向梯度
c.backward()
print("Tensor a's grad is: {}".format(a.grad))
print("Tensor b's grad is: {}".format(b.grad))
print("Tensor c's grad is: {}".format(c.grad))

Tensor a's grad is: Tensor(shape=[1], dtype=float32, place=CPUPlace, stop_gradient=False,
       [5.])
Tensor b's grad is: None
Tensor c's grad is: Tensor(shape=[1], dtype=float32, place=CPUPlace, stop_gradient=False,
       [1.])


/opt/conda/envs/python35-paddle120-env/lib/python3.7/site-packages/paddle/fluid/dygraph/varbase_patch_methods.py:392: UserWarning: [93m
Warning:
tensor.grad will return the tensor value of the gradient. This is an incompatible upgrade for tensor.grad API.  It's return type changes from numpy.ndarray in version 2.0 to paddle.Tensor in version 2.1.0.  If you want to get the numpy value of the gradient, you can use :code:`x.grad.numpy()` [0m
  warnings.warn(warning_msg)

下面我们解释下上面代码的执行逻辑。

1.3.2.1 前向执行

在上面代码中，第7行c.backward()被执行前，会为每个张量和算子创建相应的反向张量和反向函数。

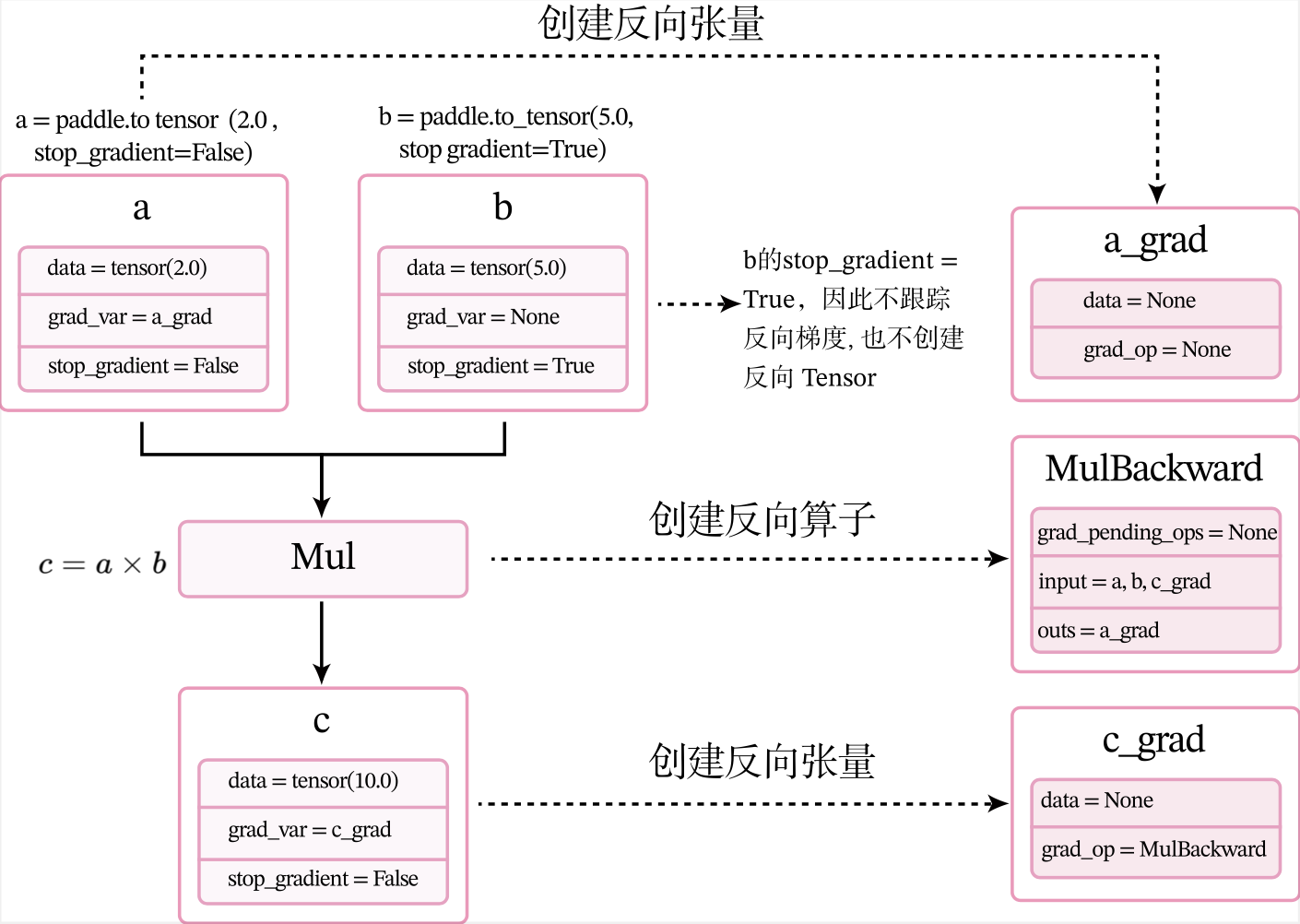
当创建张量或执行算子的前向计算时，会自动创建反向张量或反向算子。这里以上面代码中乘法为例来进行说明。

当创建张量a时，由于其属性stop_gradient=False，因此会自动为a创建一个反向张量，也就是图1.8中的a_grad。由于a不依赖其它张量或算子，a_grad的grad_op为None。
当创建张量b时，由于其属性stop_gradient=True，因此不会为b创建一个反向张量。
执行乘法\(c=a\times b\) 时，\(\times\)是一个前向算子Mul，为其构建反向算子MulBackward。由于Mul的输入是a和b，输出是c，对应反向算子MulBackward的输入是张量c的反向张量c_grad，输出是a和b的反向张量。如果输入定义stop_gradient=True，反向张量即为None。在此例子中就是a_grad和None。
反向算子MulBackward中的grad_pending_ops用于在自动构建反向网络时，明确该反向算子的下一个可执行的反向算子。可以理解为在反向计算中，该算子衔接的下一个反向算子。
当c通过乘法算子Mul被创建后，c会创建一个反向张量c_grad，它的grad_op为该乘法算子的反向算子，即MulBackward。

由于此时还没有进行反向计算，因此这些反向张量和反向算子中的具体数值为空(data = None)。此时，上面代码对应的计算图状态如图1.8所示。

图1.8 调用backward()前的计算图状态

1.3.2.2 反向执行

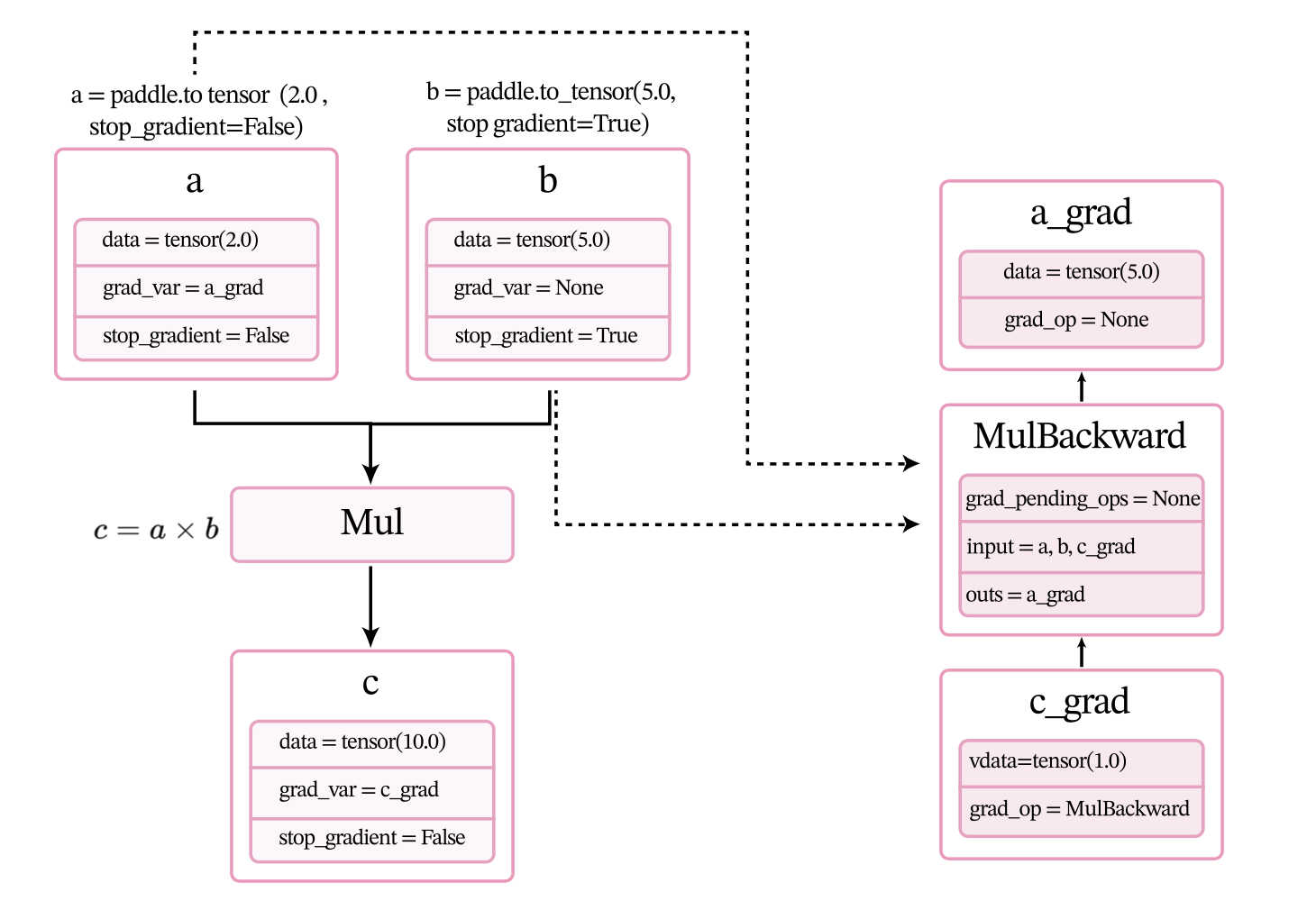
调用backward()后，执行计算图上的反向过程，即通过链式法则自动计算每个张量或算子的微分，计算过程如图1.9所示。经过自动反向梯度计算，获得c_grad和a_grad的值。

图1.9 调用backward()后的计算图状态

1.3.3 预定义的算子

从零开始构建各种复杂的算子和模型是一个很复杂的过程，在开发的过程中也难以避免地会出现很多冗余代码，因此飞桨提供了基础算子和中间算子，可以便捷地实现复杂模型。

在深度学习中，大多数模型都是以各种神经网络为主，由一系列层(Layer)组成，层是模型的基础逻辑执行单元。飞桨提供了paddle.nn.Layer类来方便快速地实现自己的层和模型。模型和层都可以基于paddle.nn.Layer扩充实现，模型只是一种特殊的层。

当我们实现的算子继承paddle.nn.Layer类时，就不用再定义backward函数。飞桨的自动微分机制可以自动完成反向传播过程，让我们只关注模型构建的前向过程，不必再进行烦琐的梯度求导。

1.3.4 本书中实现的算子

更深入的理解深度学习的模型和算法，在本书中，我们也手动实现自己的算子库：nndl，并基于自己的算子库来构建机器学习模型。本书中的自定义算子分为两类：一类是继承在第1.3.1节中定义Op类，这些算子是为了进行更好的展示模型的实现细节，需要自己动手计算并实现其反向函数；另一类是继承飞桨的paddle.nn.Layer类，更方便地搭建复杂算子，并和飞桨预定义算子混合使用。

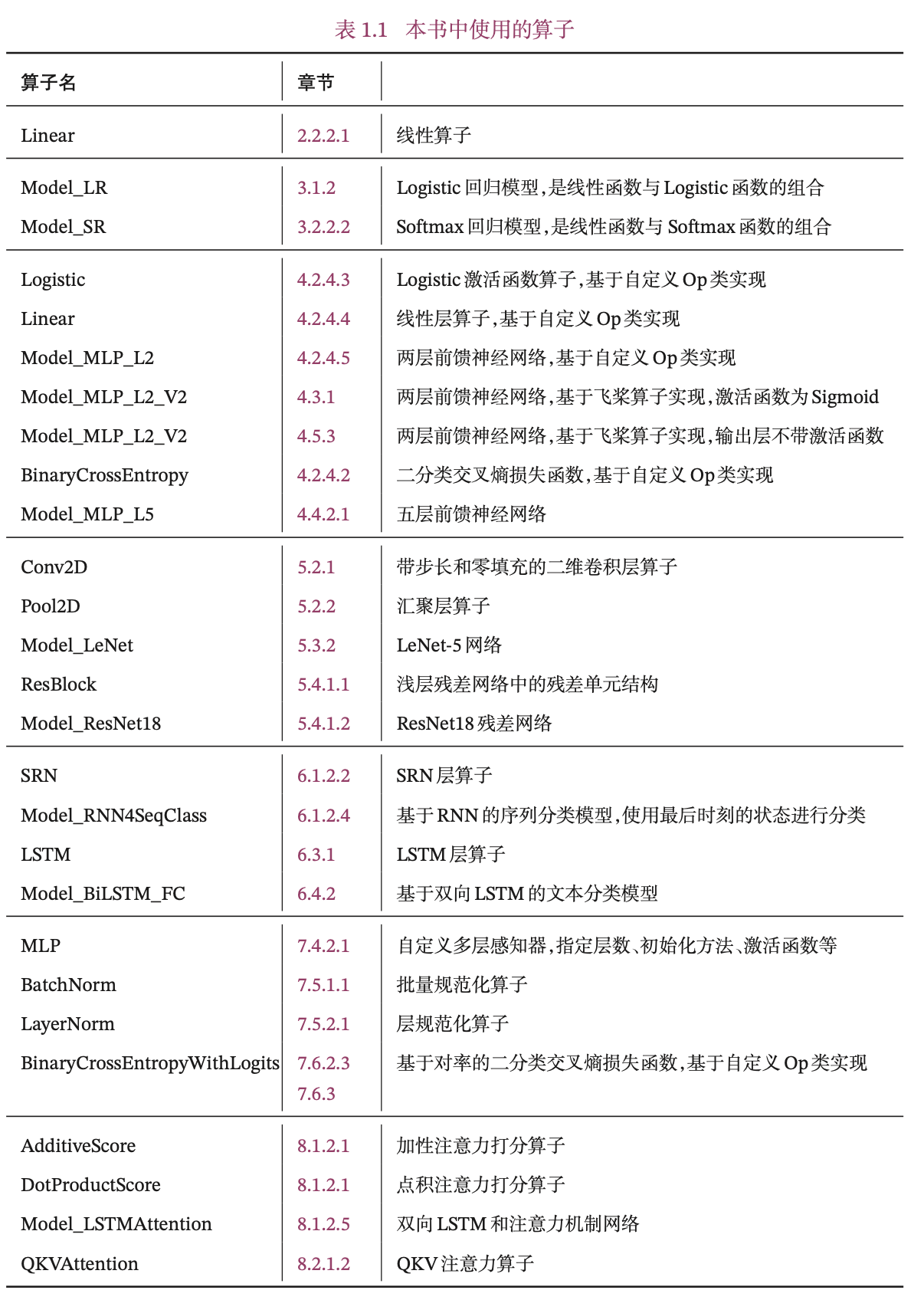
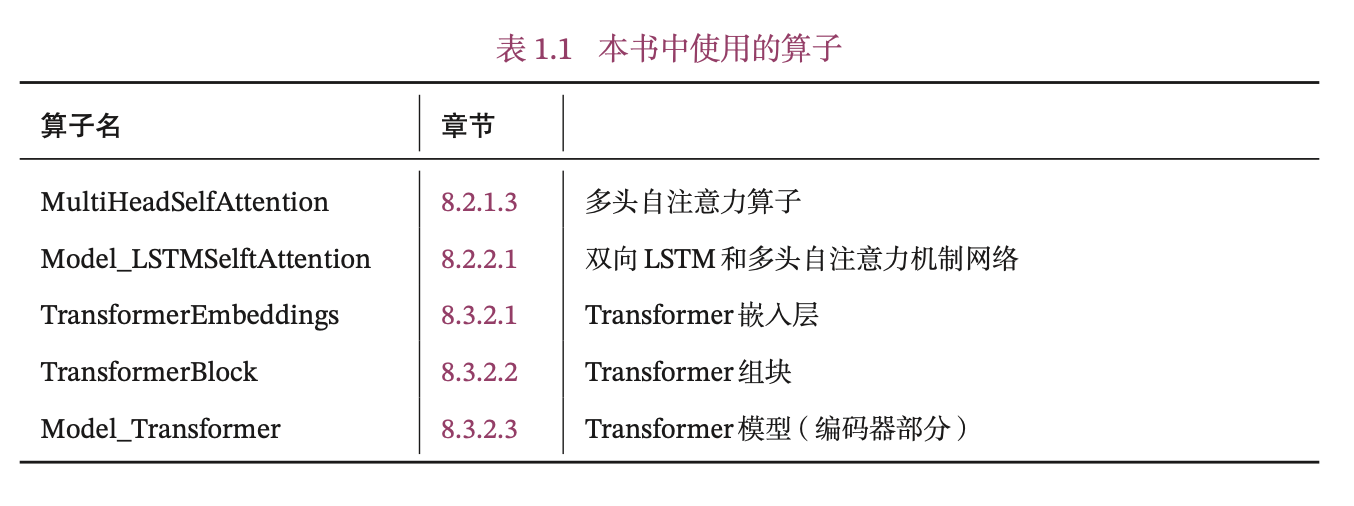
本书中实现的算子见表1.1所示，其中Model_开头为完整的模型。

表1.1 本书中使用的算子

1.3.5 本书中实现的优化器

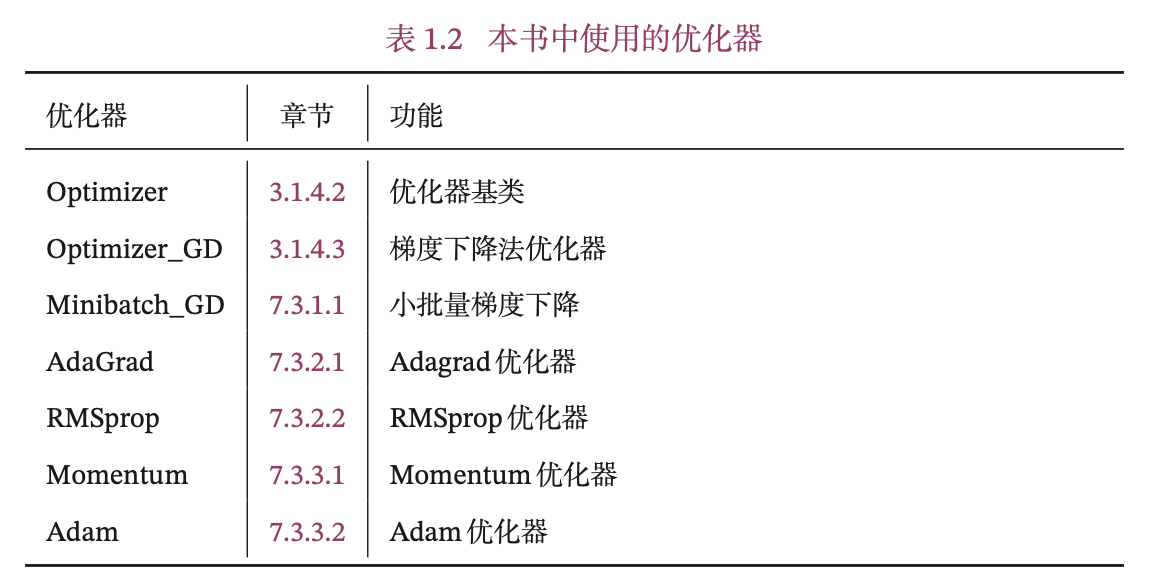
针对继承Op类的算子的优化，本书还实现了自定义的优化器，见表1.2所示。

表1.2 本书中使用的优化器

1.4 本书中实现的DataSet类

为了更好地实践，本书在模型解读部分主要使用简单任务和数据集，在案例实践部分主要使用公开的实际案例数据集。下面介绍我们用到的数据集以及对应构建的DataSet类。

1.4.1 数据集

本书中使用的数据集如下：

线性回归数据集ToyLinear150：在第2.2.1.2节中构建，用于简单的线性回归任务。ToyLinear150数据集包含150条带噪音的样本数据，其中训练集100条、测试集50条，由在第2.2.1.2节中create_toy_data函数构建。
非线性回归数据集ToySin25：在第2.3.1节中构建，用于简单的多项式回归任务.ToySin25数据集包含25条样本数据，其中训练集15条、测试集10条。ToySin25数据集同样使用在第2.2.1.1节中create_toy_data函数进行构建。
波士顿房价预测数据集：波士顿房价预测数据集共506条样本数据，每条样本包含了12种可能影响房价的因素和该类房屋价格的中位数。该数据集在第2.5节中使用。
二分类数据集Moon1000：在第3.1中构建，二分类数据集Moon1000数据是从两个带噪音的弯月形状数据分布中采样得到，每个样本包含2个特征，其中训练集640条、验证集160条、测试集200条。该数据集在本书第3.1节和第4.2节中使用。数据集构建函数make_moons在第7.4.2.3节和第7.6节中使用。
三分类数据集Multi1000：在第3.2.1节中构建三分类数据集集Multi1000，其中训练集640条、验证集160条、测试集200条。该数据集来自三个不同的簇，每个簇对应一个类别。
鸢尾花数据集：鸢尾花数据集包含了3种鸢尾花类别(Setosa、Versicolour、Virginica)，每种类别有50个样本，共计150个样本。每个样本中包含了4个属性：花萼长度、花萼宽度、花瓣长度以及花瓣宽度。该数据集在第3.3节和第4.5节使用。
MNIST数据集：MNIST手写数字识别数据集是计算机视觉领域的经典入门数据集，包含了训练集60 000条、测试集10 000条。MNIST数据集在第5.3.1节和第7.2节中使用。
CIFAR-10 数据集：CIFAR-10数据集是计算机视觉领域的经典数据集，包含了10种不同的类别、共 60 000 张图像，其中每个类别的图像都是6 000 张，图像大小均为32×32像素。CIFAR-10数据集在第5.5节中使用.
IMDB电影评论数据集：IMDB电影评论数据集是一份关于电影评论的经典二分类数据集。IMDB按照评分的高低筛选出了积极评论和消极评论，如果评分≥7，则认为是积极评论；如果评分≤4，则认为是消极评论。数据集包含训练集和测试集数据，数量各为25 000 条，每条数据都是一段用户关于某个电影的真实评价，以及观众对这个电影的情感倾向。IMDB数据集在第6.4节、第8.1节和第8.2节中使用.
数字求和数据集DigitSum：在第6.1.1节中构建，包含用于数字求和任务的不同长度的数据集。数字求和任务的输入是一串数字，前两个位置的数字为0-9，其余数字随机生成(主要为0)，预测目标是输入序列中前两个数字的加和，用来测试模型的对序列数据的记忆能力。
LCQMC通用领域问题匹配数据集：LCQMC数据集是百度知道领域的中文问题匹配数据集，目的是为了解决在中文领域大规模问题匹配数据集的缺失。该数据集从百度知道不同领域的用户问题中抽取构建数据。LCQMC数据集共包含训练集238 766条、验证集8 802条和测试集12 500 条。LCQMC数据集在第8.3节中使用。

1.4.2 Dataset类

为了更好地支持使用随机梯度下降进行参数学习，我们构建了DataSet类，以便可以更好地进行数据迭代。

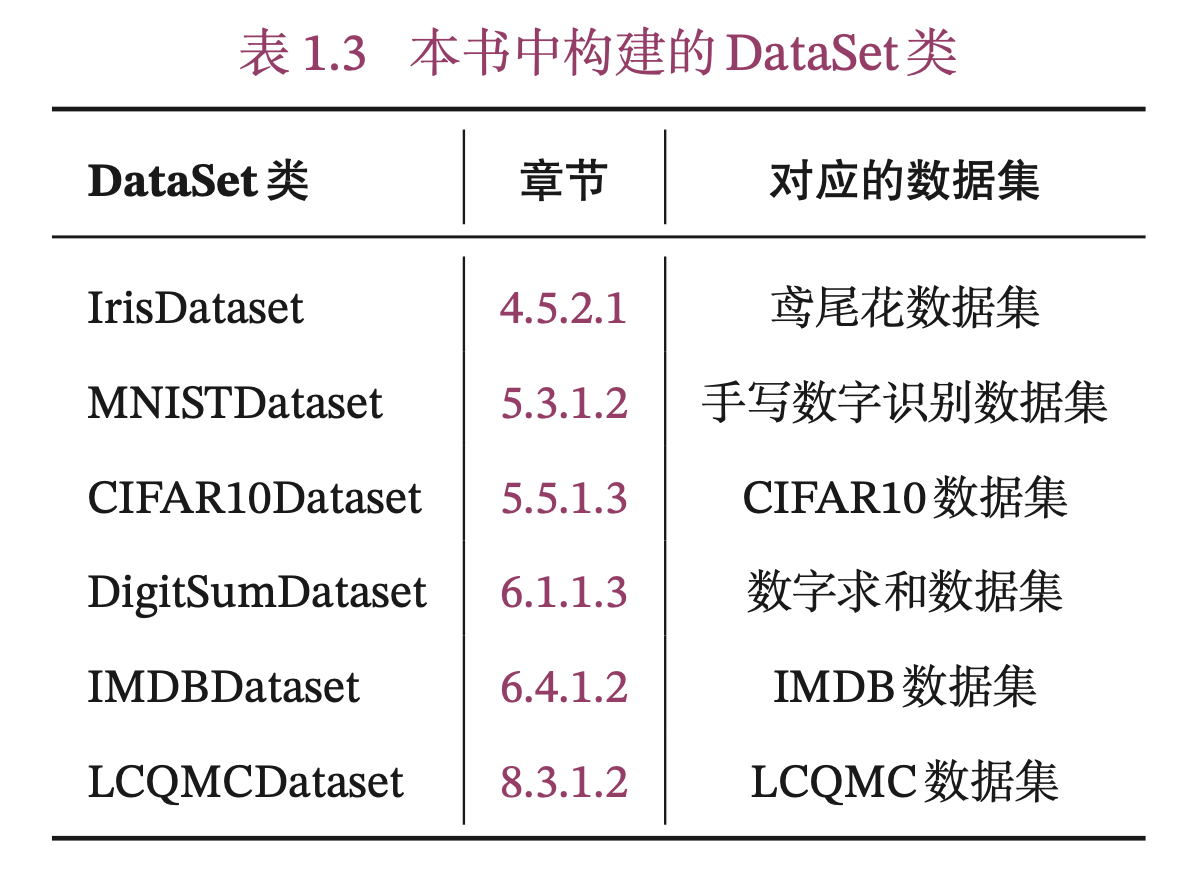
本书中构建的DataSet类见表1.3。关于Dataset类的具体介绍见第4.5.1.1节。

表1.3 本书中构建的DataSet类

1.5 本书中使用的Runner类

在一个任务上应用机器学习方法的流程基本上包括：数据集构建、模型构建、损失函数定义、优化器定义、评价指标定义、模型训练、模型评价和模型预测等环节。为了将上述环节规范化，我们将机器学习模型的基本要素封装成一个Runner类，使得我们可以更方便进行机器学习实践。除上述提到的要素外，Runner类还包括模型保存、模型加载等功能。Runner类的具体介绍可参见第2节.
这里我们对本书中用到的三个版本的Runner类进行汇总，说明每一个版本Runner类的构成方式.

RunnerV1：在第2节中实现，用于线性回归模型的训练，其中训练过程通过直接求解解析解的方式得到模型参数，没有模型优化及计算损失函数过程，模型训练结束后保存模型参数。
RunnerV2：在第3.1.6节中实现。RunnerV2主要增加的功能为：

在训练过程引入梯度下降法进行模型优化；
模型训练过程中计算在训练集和验证集上的损失及评价指标并打印，训练过程中保存最优模型。我们在第4.3.2节和第4.3.2节分别对RunnerV2进行了完善，加入自定义日志输出、模型阶段控制等功能。

RunnerV3：在第4.5.4节中实现。RunnerV3主要增加三个功能：使用随机梯度下降法进行参数优化；训练过程使用DataLoader加载批量数据；模型加载与保存中，模型参数使用state_dict方法获取，使用state_dict加载。

1.6 小结

本节介绍了我们在后面实践中需要的一些基础知识。在后续章节中，我们会逐步学习和了解更多的实践知识。此外，如需查阅张量、算子或其他飞桨的知识，可参阅飞桨的帮助文档。

posted on 2022-08-23 18:35 HBU_DAVID 阅读(449) 评论(0) 编辑收藏举报

刷新页面返回顶部

Notebook

NNDL 实验1

第1章 实践基础

1.1 如何运行本书的代码

1.1.1 本地运行

1.1.1.1 环境准备

1.1.1.2 快速安装

1.1.2 AI Studio运行

1.2 张量

1.2.1 创建张量

1.2.1.1 指定数据创建张量

1.2.1.2 指定形状创建

1.2.1.3 指定区间创建

1.2.2 张量的属性

1.2.2.1 张量的形状

1.2.2.2 形状的改变

1.2.2.3 张量的数据类型

1.2.2.4 张量的设备位置

1.2.3 张量与Numpy数组转换

1.2.4 张量的访问

1.2.4.1 索引和切片

1.2.4.2 访问张量

1.2.4.3 修改张量

1.2.5 张量的运算

1.2.5.1 数学运算

1.2.5.2 逻辑运算

1.2.5.3 矩阵运算

1.2.5.4 广播机制

广播机制的条件

广播机制的计算规则

1.3 算子

1.3.1 算子定义

1.3.1.1 加法算子

前向计算

反向计算

1.3.1.2 乘法算子

1.3.1.3 指数算子

1.3.2 自动微分机制

1.3.2.1 前向执行

1.3.2.2 反向执行

1.3.3 预定义的算子

1.3.4 本书中实现的算子

1.3.5 本书中实现的优化器

1.4 本书中实现的DataSet类

1.4.1 数据集

1.4.2 Dataset类

1.5 本书中使用的Runner类

1.6 小结

导航

第1章实践基础