神经网络与深度学习（邱锡鹏）编程练习4 FNN 反向传播 梯度下降 pytorch

题目介绍，见：神经网络与深度学习（邱锡鹏）编程练习4 FNN 反向传播 梯度下降 numpy - HBU_DAVID - 博客园 (cnblogs.com)

 

用框架，省时省力。

numpy实现：紧扣理论，推导公式，实现公式。计算机相关专业必须掌握底层理论。

pytorch实现：框架降低了DL编程门槛，减轻了程序员负担，提高了编程效率。 backward( )、optim.SGD( )免去了繁琐的BP、GD计算过程。

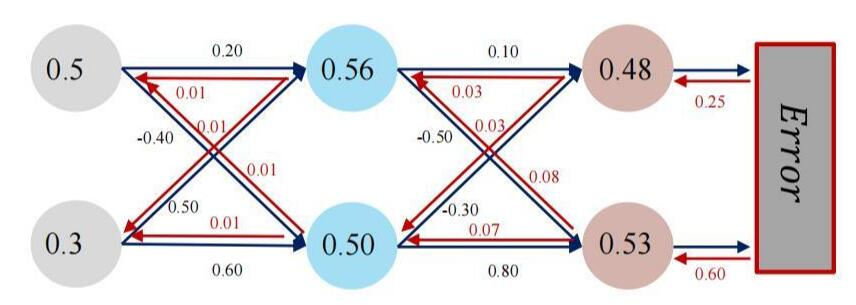
实验源码使用了 Sigmoid + MSE + SGD 

实验要求：读懂实验源代码，跟numpy源代码作比较，并尝试以下工作：

1. 激活函数Sigmoid改变为Relu，观察、总结并陈述。
2. 损失函数MSELoss()交叉熵 torch.nn.BCELoss()，观察、总结并陈述。
3. 改变步长（学习率），训练次数，观察、总结并陈述。
4. 权值不初始化。即：删除w1-w8初始值。对比 权值初始化 和 权值不初始化 结果，观察、总结并陈述。
5. 优化器SGD（随机梯度下降），换成Adam试试。观察、总结并陈述。 
6. 全面总结反向传播原理和编码实现，认真写心得体会。

 

import torch
import torch.nn as nn
import torch.optim as optim
import matplotlib.pyplot as plt


class Net(nn.Module):
    # 初始化网络结构
    def __init__(self, input_size, hidden_size, num_classes):
        super(Net, self).__init__()
        # print(input_size, hidden_size, num_classes)
        self.fc1 = nn.Linear(input_size, hidden_size)  # 输入层，线性（liner）关系
        self.sigmoid = torch.nn.Sigmoid()  # 隐藏层，使用ReLU函数
        self.fc2 = nn.Linear(hidden_size, num_classes)  # 输出层，线性（liner）关系

    # forward 参数传递函数，网络中数据的流动
    def forward(self, x, w1, w2):
        self.fc1.weight.data = w1
        self.fc1.bias.data = torch.Tensor([0.0])
        out = self.fc1(x)
        out = self.sigmoid(out)
        self.fc2.weight.data = w2
        self.fc2.bias.data = torch.Tensor([0.0])
        out = self.fc2(out)
        out = self.sigmoid(out)
        return out


net = Net(2, 2, 2)

if __name__ == "__main__":
    x = torch.tensor([0.5, 0.3])
    y = torch.tensor([0.23, -0.07])  # y0, y1 = 0.23, -0.07
    w1 = torch.Tensor([[0.2, 0.5], [-0.4, 0.6]])    # 一般情况下，参数无需初始化，让机器自己学习。 有时，初始化参数可提高效率。
    w2 = torch.Tensor([[0.1, -0.3], [-0.5, 0.8]])
    w1.requires_grad = True
    w2.requires_grad = True

    eli = []
    lli = []
    loss_fuction = torch.nn.MSELoss()  # 使用pytorch的MSE
    optimizer = optim.SGD(net.parameters(), lr=1)  # 优化函数：随机梯度下降
    for i in range(10):
        print("=====第" + str(i) + "轮=====")
        y_pred = net(x, w1, w2)  # 前向传播
        L = loss_fuction(y_pred, y)  #
        print("损失函数：", L.data)
        L.backward()  # 反向传播，求出计算图中所有梯度存入w中
        optimizer.step()  # 自动更新参数. 不需要人工编程实现。

        eli.append(i)
        lli.append(L.data.numpy())

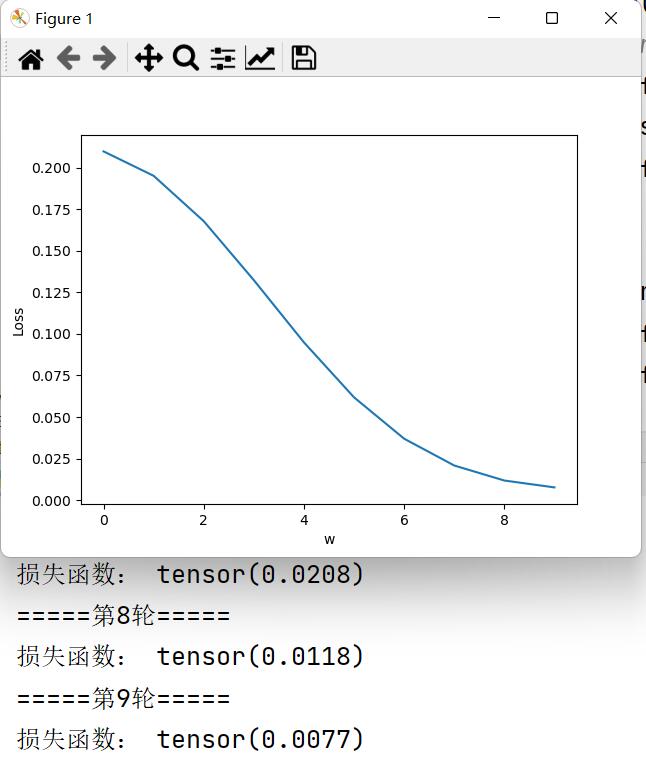
    plt.plot(eli, lli)
    plt.ylabel('Loss')
    plt.xlabel('w')
    plt.show()