神经网络与深度学习(邱锡鹏)编程练习 2 线性回归的参数优化 基函数回归 Jupyter导出版
ref:https://www.cnblogs.com/douzujun/p/13282073.html
按照“填空顺序编号”分别完成“参数优化”,“不同基函数”的实现
import numpy as np
import matplotlib.pyplot as plt
def load_data(filename):
"""载入数据。"""
xys = []
with open(filename, 'r') as f:
for line in f:
xys.append(map(float, line.strip().split()))
xs, ys = zip(*xys)
return np.asarray(xs), np.asarray(ys)
不同的基函数 (basis function)的实现
填空顺序 2: 请分别在这里实现“多项式基函数”以及“高斯基函数”
其中以及训练集的x的范围在0-25之间
def identity_basis(x):
print("线性回归")
ret = np.expand_dims(x, axis=1)
return ret
def multinomial_basis(x, feature_num=10):
print("多项式基函数")
x = np.expand_dims(x, axis=1) # shape(N, 1)
feat = [x]
for i in range(2, feature_num+1):
feat.append(x**i)
ret = np.concatenate(feat, axis=1)
return ret
def gaussian_basis(x, feature_num=10):
print("高斯基函数")
centers = np.linspace(0, 25, feature_num)
width = 1.0 * (centers[1] - centers[0])
x = np.expand_dims(x, axis=1)
x = np.concatenate([x]*feature_num, axis=1)
out = (x-centers)/width
ret = np.exp(-0.5 * out ** 2)
return ret
返回一个训练好的模型
填空顺序 1 用最小二乘法进行模型优化
填空顺序 3 用梯度下降进行模型优化
先完成最小二乘法的优化 (参考书中第二章 2.3中的公式)
再完成梯度下降的优化 (参考书中第二章 2.3中的公式)
在main中利用训练集训练好模型的参数,并且返回一个训练好的模型。
计算出一个优化后的w,请分别使用最小二乘法以及梯度下降两种办法优化w
def main(x_train, y_train):
"""
训练模型,并返回从x到y的映射。
【注意】basis_func 三选一。用一个,注释掉其他两个。
"""
# basis_func = identity_basis # 线性回归
# basis_func = multinomial_basis # 多项式基函数
basis_func = gaussian_basis # 高斯基函数
phi0 = np.expand_dims(np.ones_like(x_train), axis=1)
phi1 = basis_func(x_train)
phi = np.concatenate([phi0, phi1], axis=1)
# 【注意】最小二乘 和 梯度下降 ,选用一个,注释掉另一个。
#========== '''计算出一个优化后的w,最小二乘法优化w'''
# w = np.dot(np.linalg.pinv(phi), y_train) # np.linalg.pinv(phi)求phi的伪逆矩阵(phi不是列满秩) w.shape=[2,1]
#========== '''计算出一个优化后的w,梯度下降优化w'''
def dJ(theta, phi, y):
return phi.T.dot(phi.dot(theta)-y)*2.0/len(phi)
def gradient(phi, y, initial_theta, eta=0.001, n_iters=10000):
w = initial_theta
for i in range(n_iters):
gradient = dJ(w, phi, y) #计算梯度
w = w - eta *gradient #更新w
return w
initial_theta = np.zeros(phi.shape[1])
w = gradient(phi, y_train, initial_theta)
#==========
def f(x):
phi0 = np.expand_dims(np.ones_like(x), axis=1)
phi1 = basis_func(x)
phi = np.concatenate([phi0, phi1], axis=1)
y = np.dot(phi, w)
return y
return f
评估结果
没有需要填写的代码,但是建议读懂
def evaluate(ys, ys_pred):
"""评估模型。"""
std = np.sqrt(np.mean(np.abs(ys - ys_pred) ** 2))
return std
# 程序主入口(建议不要改动以下函数的接口)
if __name__ == '__main__':
train_file = 'train.txt'
test_file = 'test.txt'
# 载入数据
x_train, y_train = load_data(train_file)
x_test, y_test = load_data(test_file)
print(x_train.shape)
print(x_test.shape)
# 使用线性回归训练模型,返回一个函数f()使得y = f(x)
f = main(x_train, y_train)
y_train_pred = f(x_train)
std = evaluate(y_train, y_train_pred)
print('训练集预测值与真实值的标准差:{:.1f}'.format(std))
# 计算预测的输出值
y_test_pred = f(x_test)
# 使用测试集评估模型
std = evaluate(y_test, y_test_pred)
print('预测值与真实值的标准差:{:.1f}'.format(std))
#显示结果
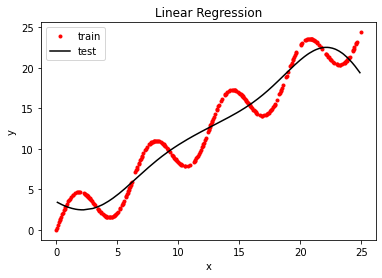
plt.plot(x_train, y_train, 'ro', markersize=3)
# plt.plot(x_test, y_test, 'k')
plt.plot(x_test, y_test_pred, 'k')
plt.xlabel('x')
plt.ylabel('y')
plt.title('Linear Regression')
plt.legend(['train', 'test', 'pred'])
plt.show()
(300,)
(200,)
高斯基函数
高斯基函数
训练集预测值与真实值的标准差:1.9
高斯基函数
预测值与真实值的标准差:2.1