维特比算法 Viterbi
维特比算法
-
一种动态规划算法(动态规划 Dynamic Programming,是运筹学的一个分支,是求解决策过程最优化的过程。)
-
用于寻找最有可能产生观测事件序列的-维特比路径-隐含状态序列
-
特别是在马尔可夫信息源上下文和隐马尔可夫模型中
在计算机科学领域,应用动态规划的思想解决的最基本的一个问题就是:寻找有向无环图(篱笆网络Lattice)中两个点之间的最短路径。
从两个点之间找一条最短的路径,除了遍历完所有路径,还有什么更好的方法?答案:viterbi (维特比)算法。
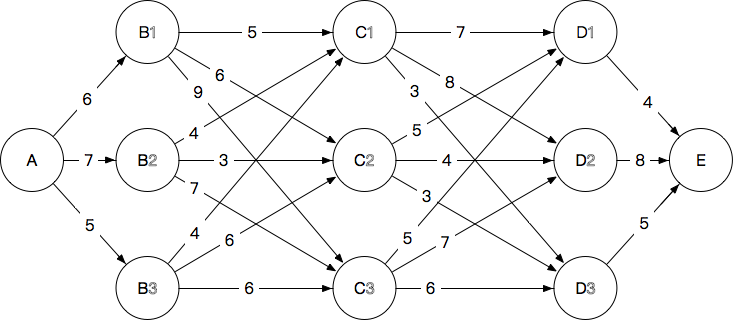
A→E 的最短路径
穷举法(遍历):每条路径需要计算4次加法,共3×3×3=27条路径,共4×27=108次计算。
维特比算法需要多少次计算?
A→B
6,7, 5
A→B→C
C1: 6+5=11,7+4=11,5+4=09, 最终选择A→B3→C1,抛弃其他到C1的路径,长度09
C2: 6+6=12,7+3=10,5+6=11, 最终选择A→B2→C2,抛弃其他到C2的路径,长度10
C3: 6+9=15,7+7=14,5+6=11, 最终选择A→B3→C3,抛弃其他到C3的路径,长度11
A(→B)→C→D
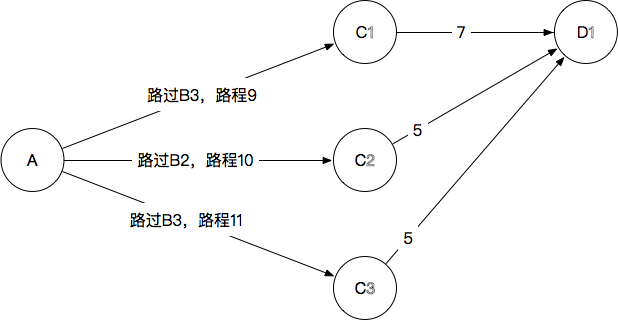

D1:9+7=16,10+5=15,11+5=16,最终选择A→B2→C2→D1,抛弃其他到D1的路径,长度15
D2:9+8=17,10+4=14,11+7=18,最终选择A→B2→C2→D2,抛弃其他到D2的路径,长度14
D3:9+3=12,10+3=13,11+6=17,最终选择A→B3→C1→D3,抛弃其他到D3的路径,长度12
A(→B→C)→D→E
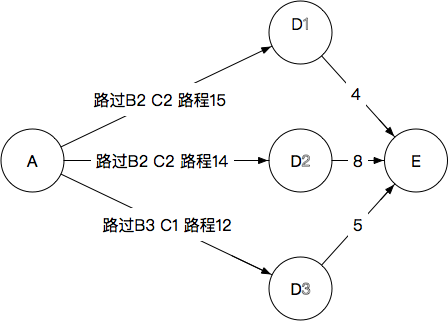

15+4=19
14+8=22
12+5=17
选择D3
完整路径: A→B3→C1→D3→E
计算的次数大约是多少?
从A到B有3条路径,每一条需要算到每一个C的最短距离,所以是:2(路径加法数)×3(A→B)×3(B→C)=18,
确定了每一个到C的最短距离,剩下的事情就可以从C开始考虑:每一个C需要确定到每一个D的最短距离:2(路径加法数)×3(C个数)×3(D个数)=18,
最终再加上D到E的距离:2×3=6
总计:18+18+3=39
远远小于穷举法的108次
核心思想:步步为营
每一步把最短路径找出来,以后就不必再重新计算这一步,节约了时间。
类似于DB优化中的选择尽量先做,没必要带着一堆没用的数据“负重前行”。
初始状态:
P(身体状态=正常)=0.7
P(身体状态=轻感冒)=0.2
P(身体状态=重感冒)=0.1
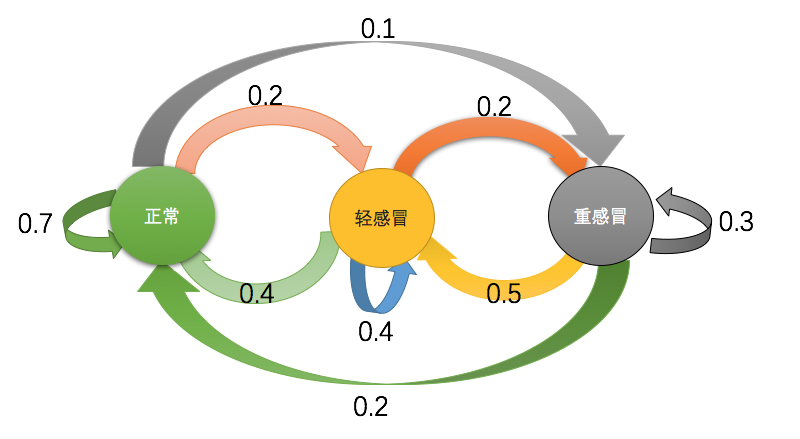
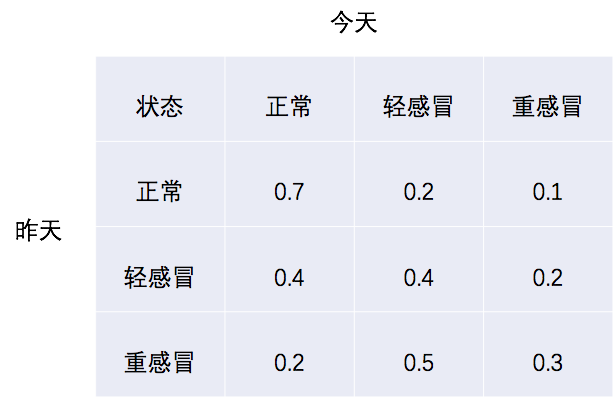
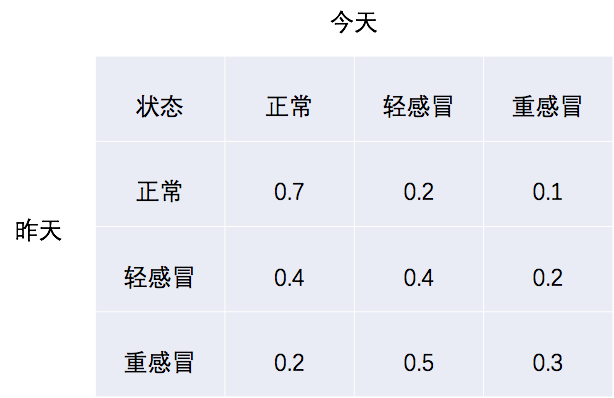
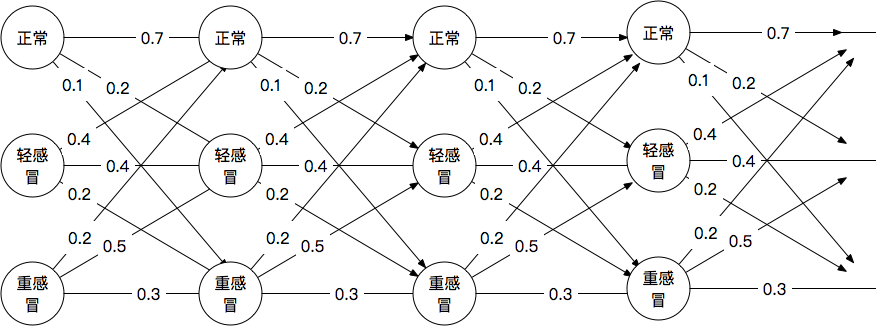
状态转移矩阵

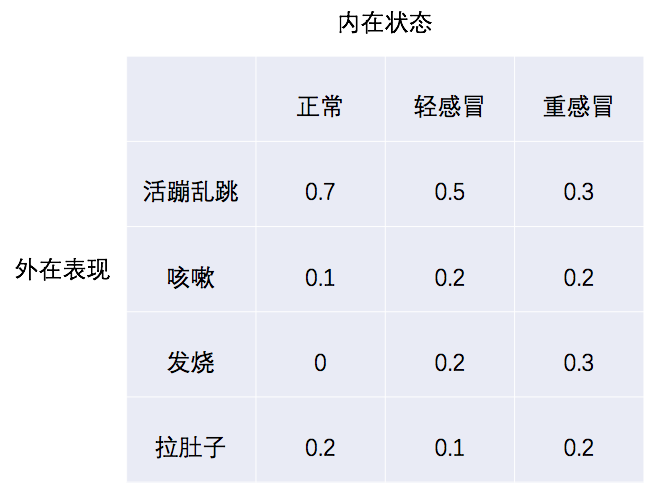
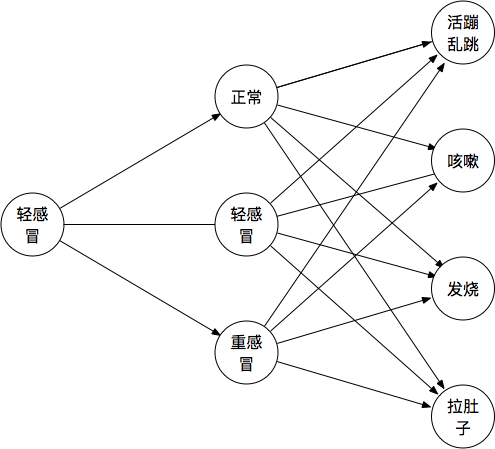
发散矩阵
观测序列:(咳嗽、发烧、拉肚子、活蹦乱跳)
问题:
已知观测序列,求这个人的状态序列
代码解决问题:
# https://blog.csdn.net/Luzichang/article/details/91365752 import math # 状态的样本空间 states = ('没毛病','轻感冒','重感冒') # 观测的样本空间 observations = ( '活跃', '咳嗽','发烧','腹泻') #observations = ( '读书', '读书','读书','读书') #observations = ( '打球', '打球','打球','打球') #observations = ( '访友', '访友','访友','访友') #observations = ( '访友', '访友','读书','访友', '访友','访友','读书') # 起始个状态概率 start_probability = {'没毛病':0.7, '轻感冒':0.2,'重感冒':0.1} # 状态转移概率 transition_probability = { '没毛病': {'没毛病':0.7, '轻感冒':0.2,'重感冒':0.1}, '轻感冒': {'没毛病':0.4, '轻感冒':0.4,'重感冒':0.2}, '重感冒': {'没毛病':0.2, '轻感冒':0.5,'重感冒':0.3}, } # 状态->观测的发散概率 emission_probability = { '没毛病': { '活跃': 0.7,'咳嗽': 0.1, '发烧': 0.0, '腹泻': 0.2}, '轻感冒': { '活跃': 0.5,'咳嗽': 0.2, '发烧': 0.2, '腹泻': 0.1}, '重感冒': { '活跃': 0.3,'咳嗽': 0.2, '发烧': 0.3, '腹泻': 0.2}, } # 计算以E为底的幂 def E(x): #return math.pow(math.e,x) return x def display_result(observations,result_m):#较为友好清晰的显示结果 # 从结果中找出最佳路径 #print(result_m) infered_states = [] final = len(result_m) - 1 (p, pre_state), final_state = max(zip(result_m[final].values(), result_m[final].keys())) infered_states.insert(0, final_state) infered_states.insert(0, pre_state) for t in range(final - 1, 0, -1): _, pre_state = result_m[t][pre_state] infered_states.insert(0, pre_state) print(format("Viterbi Result", "=^80s")) head = format("观测序列", " ^7s") head += format("推断状态", " ^16s") for s in states: head += format(s, " ^15s") print(head) print(format("", "-^80s")) for obs,result,infered_state in zip(observations,result_m,infered_states): item = format(obs," ^10s") item += format(infered_state," ^18s") for s in states: item += format(result[s][0]," >12.8f") if infered_state == s: item += "(*)" else: item +=" " print(item) print(format("", "=^80s")) def viterbi(obs, states, start_p, trans_p, emit_p): result_m = [{}] # 存放结果,每一个元素是一个字典,每一个字典的形式是 state:(p,pre_state) # 其中state,p分别是当前状态下的概率值,pre_state表示该值由上一次的那个状态计算得到 for s in states: # 对于每一个状态 result_m[0][s] = (E(start_p[s]*emit_p[s][obs[0]]),None) # 把第一个观测节点对应的各状态值计算出来 #print('11',result_m[0][s]) for t in range(1,len(obs)): result_m.append({}) # 准备t时刻的结果存放字典,形式同上 for s in states: # 对于每一个t时刻状态s,获取t-1时刻每个状态s0的p,结合由s0转化为s的转移概率和s状态至obs的发散概率 # 计算t时刻s状态的最大概率,并记录该概率的来源状态s0 # max()内部比较的是一个tuple:(p,s0),max比较tuple内的第一个元素值 result_m[t][s] = max([(E(result_m[t-1][s0][0]*trans_p[s0][s]*emit_p[s][obs[t]]),s0) for s0 in states]) #print(result_m[t][s]) return result_m # 所有结果(包括最佳路径)都在这里,但直观的最佳路径还需要依此结果单独生成,在显示的时候生成 if __name__ == "__main__": result_m = viterbi( observations, states, start_probability, transition_probability, emission_probability) display_result(observations,result_m)
输出结果如下:
=================================Viterbi Result================================= 观测序列 推断状态 没毛病 轻感冒 重感冒 -------------------------------------------------------------------------------- 活跃 没毛病 0.49000000(*) 0.10000000 0.03000000 咳嗽 轻感冒 0.03430000 0.01960000(*) 0.00980000 发烧 轻感冒 0.00000000 0.00156800(*) 0.00117600 腹泻 没毛病 0.00012544(*) 0.00006272 0.00007056 ================================================================================
结果分析:
递推过程,顺向。选择每一步最短路径(最大概率),然后进行下一步。步步为营。
注意:“每一步的最短路径”不是“最终的最短路径”,“最终的最短路径”是回溯得到的。
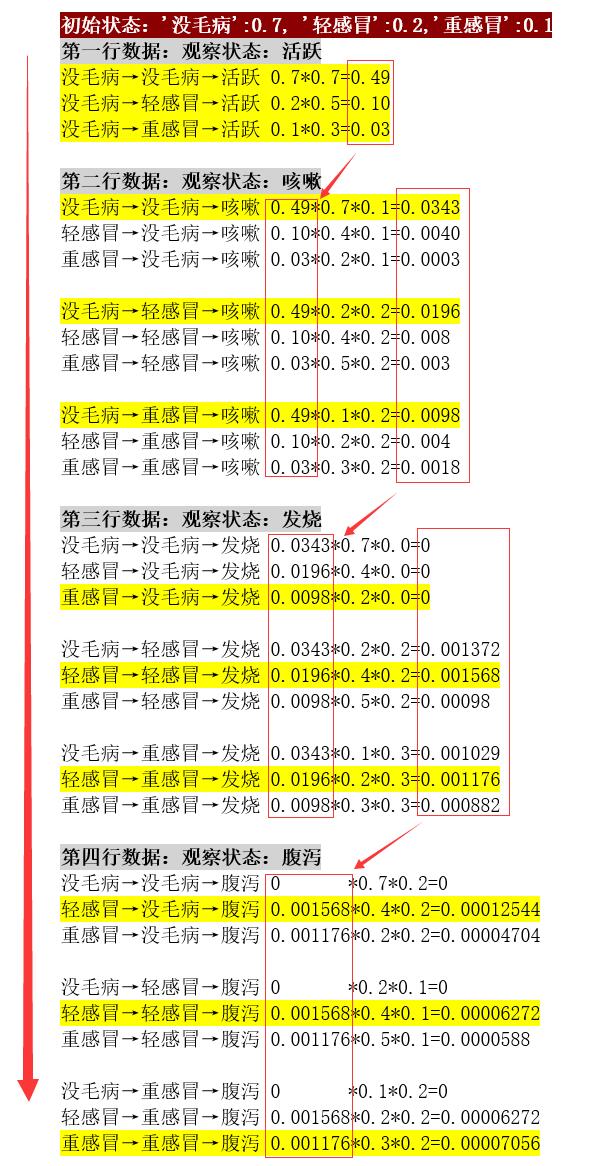
回溯过程,逆向。找到最终结果的最大概率,然后逆流而上,继续找上一步的最大概率,形成一条链路,这条链路就是“最终的最短路径”。
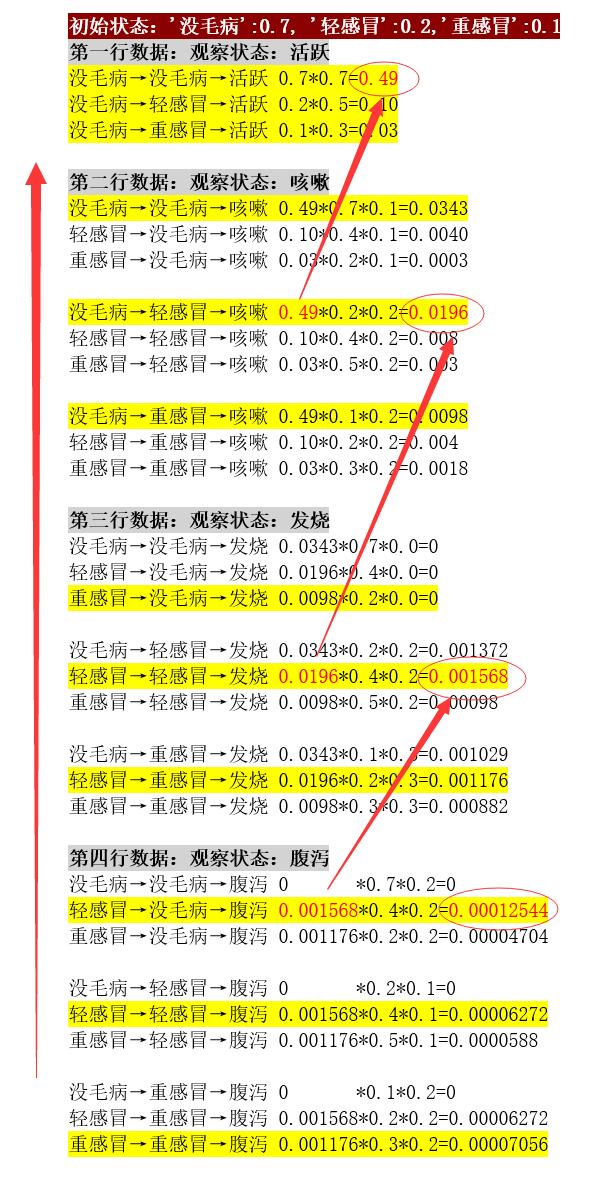
REF:

————————————————
REF:
https://blog.csdn.net/athemeroy/article/details/79339546
https://www.zhihu.com/question/20136144
posted on 2020-07-05 18:39 HBU_DAVID 阅读(1039) 评论(0) 编辑 收藏 举报




