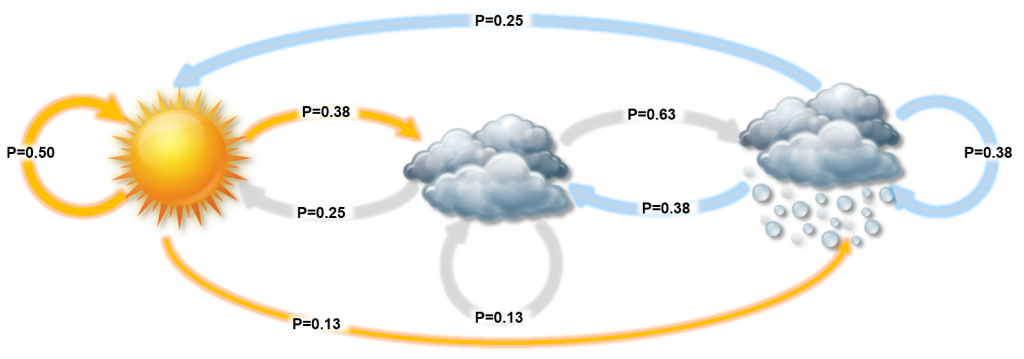
隐马尔可夫模型(Hidden Markov model, HMM)
开篇就是“大量公式+抽象算法+密密麻麻文字”的帖子,实在是读不下去。
网上搜搜讲的有趣点的,有图的,例子计较通俗易懂的。
不要一开篇就是 \(x_1,x_2 ...,x_n\) ,非常打击积极性。
循序渐进,从具体的例子,慢慢的再到抽象的公式。
阶梯型的学习,才是正确的学习方法。

隐马模型(Hidden Markov model, HMM)
- 结构最简单的动态贝叶斯网的生成模型
- 著名的有向图模型
- 典型的自然语言中处理标注问题的统计机器学模型
隐马模型发明者:不是马尔科夫,而是鲍姆(【Leonard Esau Baum】 August 23, 1931 – August 14, 2017)
鲍姆-韦尔奇算法(Baum-Welch算法)
https://www.cnblogs.com/skyme/p/4651331.html
骰子举例,讲的挺好
假设三个不同的骰子。
- 第一个骰子是我们平常见的骰子(称这个骰子为D6),6个面,每个面(1,2,3,4,5,6)出现的概率是1/6。
- 第二个骰子是个四面体(称这个骰子为D4),每个面(1,2,3,4)出现的概率是1/4。
- 第三个骰子有八个面(称这个骰子为D8),每个面(1,2,3,4,5,6,7,8)出现的概率是1/8。
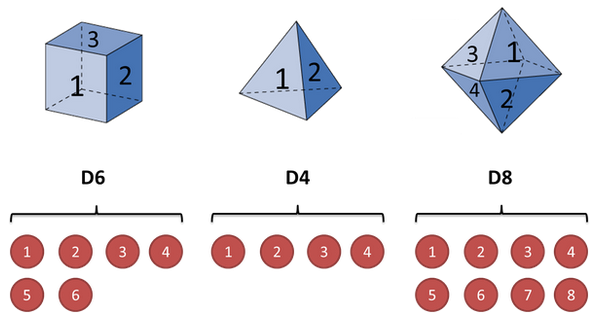
开始掷骰子,先从三个骰子里挑一个,挑到每一个骰子的概率都是1/3。
继续掷骰子,得到一个数字,1,2,3,4,5,6,7,8中的一个。
不停的重复上述过程,我们会得到一串数字,每个数字都是1,2,3,4,5,6,7,8中的一个。
可能得到这么一串数字(掷骰子10次):1 6 3 5 2 7 3 5 2 4 ,这串数字叫做可见状态链。
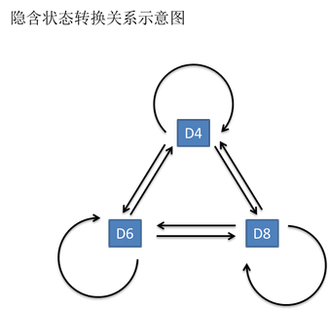
但是在隐马尔可夫模型中,不仅仅有这么一串可见状态链,还有一串隐含状态链。
在这个例子里,这串隐含状态链就是你用的骰子的序列。比如,隐含状态链有可能是:D6 D8 D8 D6 D4 D8 D6 D6 D4 D8 。
一般来说,HMM中说到的马尔可夫链其实是指隐含状态链,因为隐含状态(骰子)之间存在转换概率(transition probability)。
在我们这个例子里,D6的下一个状态是D4,D6,D8的概率都是1/3。D4,D8的下一个状态是D4,D6,D8的转换概率也都一样是1/3。
这样设定是为了最开始容易说清楚,但是我们其实是可以随意设定转换概率的。
比如,我们可以这样定义,D6后面不能接D4,D6后面是D6的概率是0.9,是D8的概率是0.1。
这样就是一个新的HMM。
同样的,尽管可见状态之间没有转换概率,但是隐含状态和可见状态之间有一个概率叫做输出概率(emission probability)。
就我们的例子来说,六面骰(D6)产生1的输出概率是1/6。产生2,3,4,5,6的概率也都是1/6。
我们同样可以对输出概率进行其他定义。比如,我有一个被赌场动过手脚的六面骰子,掷出来是1的概率更大,是1/2,掷出来是2,3,4,5,6的概率是1/10。

https://blog.csdn.net/z2536083458/article/details/99696875
较为经典的讲解
简单描述一下这个例子:
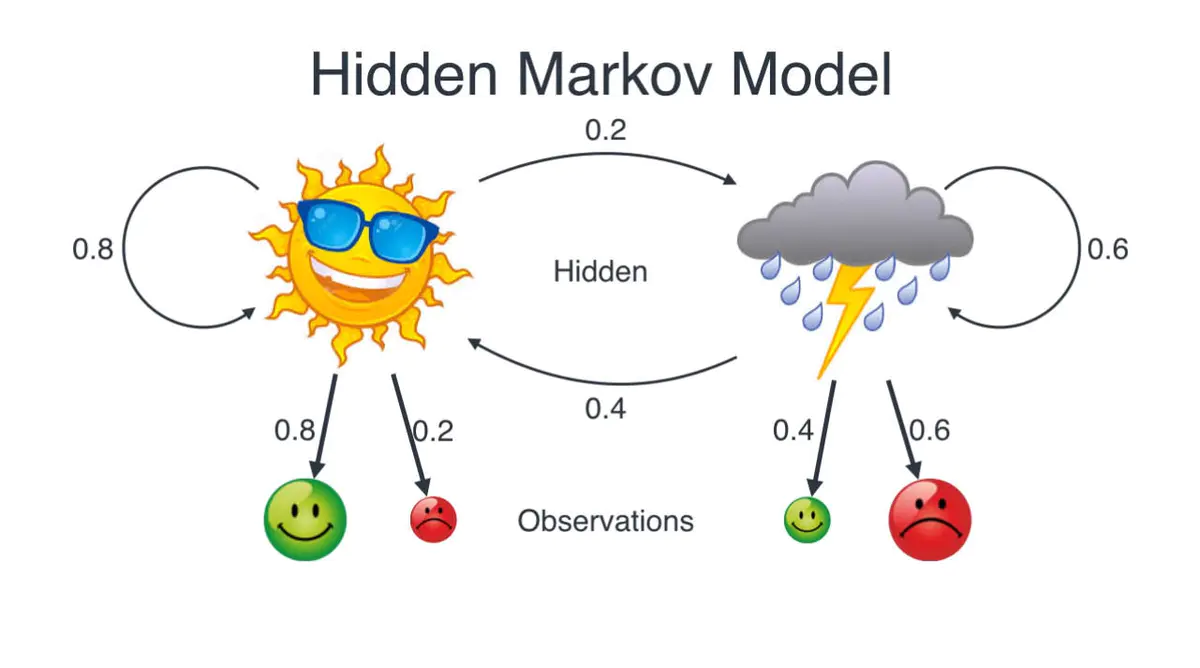
假设A与B是两个处于不同地方的朋友,
A关心B每天干了什么事情(观测序列)「散步,购物,大扫除」,
想要通过B干的事情去推断出B处地的天气变化(隐藏序列)「晴天,雨天」
隐藏序列集合:\(S_{hidden}=\{晴天,雨天\}\)
观测序列集合:\(S_{observations}=\{散步,购物,大扫除\}\)
初始状态概率矩阵:
\(M_{start\_probability}=\{雨天:0.6,晴天:0.4\}\)
状态转移矩阵:
\(M_{transition\_probability}=\{雨天:\{晴天:0.3,雨天:0.7\},晴天:\{晴天:0.6,雨天:0.4\}\}\)
发射概率矩阵:
\(M_{emission\_probability}=\{雨天:\{散步:0.1,购物:0.4,大扫除:0.5\},晴天:\{散步:0.6,购物:0.3,大扫除:0.1\}\}\)
隐藏序列:表示无法直接观测到的状态,就上述例子而言就是对方的天气状态;
观测序列:可以直接观测到的状态,就上述例子而言就是获取到的B执行的事情;
初始状态概率矩阵:表示B第一次告诉A的时候,得到的隐藏状态集合中每个状态发生的概率;
状态转移矩阵:表示从一个状态到另一个状态变化的概率,如在上述例子中,从雨天到晴天的概率为0.3;
发射状态矩阵:表示B在相应隐藏状态(天气)下,去执行得到观测状态(执行的动作)的概率,如在雨天,B去散步的概率为0.1;
HMM模型综上描述起来就是五个要素:
两个序列:隐藏序列、观测序列
三个矩阵:初始状态矩阵、发射状态矩阵、状态转移矩阵
https://www.jianshu.com/p/e6a2282089f8
配图很棒,值得一读
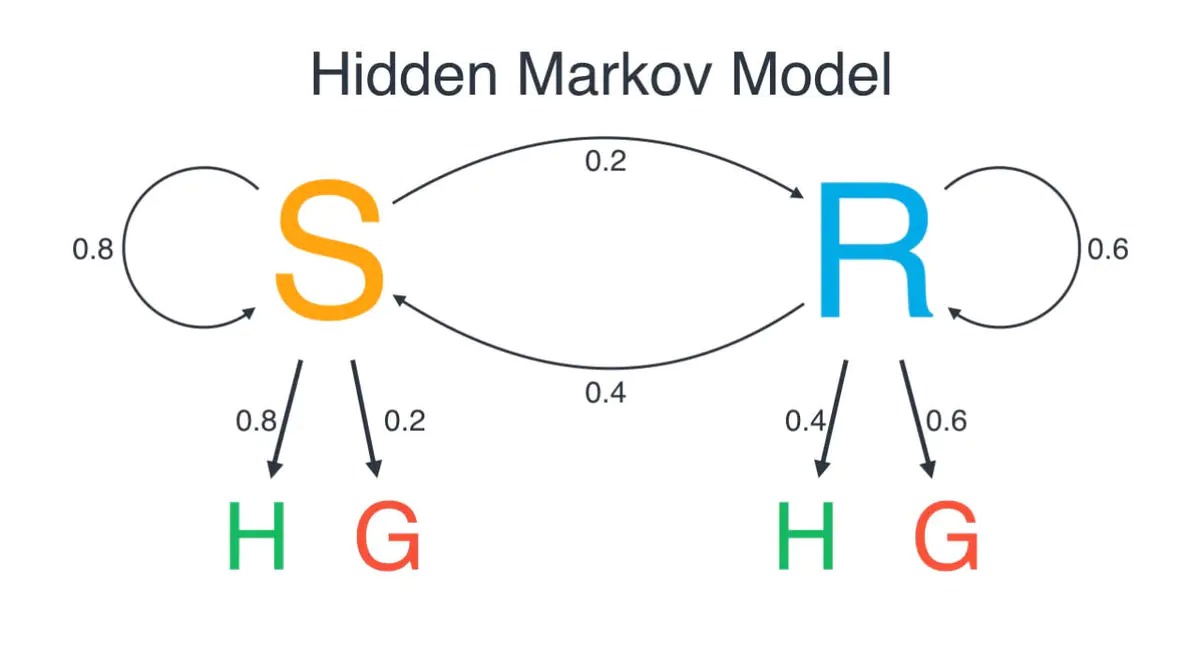
https://www.jianshu.com/p/ca483c79182e
带有算法实现,编程演示,cool~
http://bluewhale.cc/2016-06-02/hidden-markov-model-1.html
图文并茂,推荐