概率论与数理统计基础<1>:随机事件与随机变量

Part1. 随机事件

1-1.随机试验

随机试验:可以在相同条件下重复进行，每次试验的结果不止一个，事先知道所有可能的结果但不确定是哪一个的试验。
举例：重复的抛出一枚均匀的硬币就是一个随机试验，事先知道它的结果，但是不知道究竟是正面还是反面。

1-2.随机事件

定义1：随机试验可能的结果，称为样本空间，它的子集就叫做随机事件。
定义2：在一定条件下，可能发生也可能不发生的事件叫做随机事件。
举例：抛出硬币后可能正面落地，可能反面落地，那么“抛出硬币后正面落地”就是一个随机事件，它可能发生，也可能不发生。

1-3.频率与概率

频率：\(n\)次重复试验，事件A发生的次数为\(n_A\)，则\(n_A/n\)就是事件A发生的频率。
概率：当重复试验次数n越来越大时，事件A发生的频率\(n_A/n\)就会越来越稳定于一个常数；当试验次数趋向无穷大时，频率就等于这个常数，这个常数就被称为概率。
概率是一个随机事件的固有属性，它代表一个随机事件发生的可能程度，而频率是一个随机事件在一系列试验中发生的结果情况，是一个统计值。

1-4.古典概型（等可能概型）

古典概型：如果一个随机试验的结果有限，并且每一种结果发生的可能性相同，那么这个概率模型就是古典概型，也称为等可能概型。

1-5.条件概率与全概率

条件概率：

\[P(B|A)=\frac{P(AB)} {P(A)}, 其中P(A)>0 \]

事件A发生的情况下事件B发生的概率，称为条件概率。
全概率：

\[P(A)=P(A|B_1)P(B_1)+P(A|B_2)P(B_2)+…+P(A|B_n)P(B_n) \]

其中，\(B_i \cap B_j= \emptyset,i \neq j,i,j=1,2…n;B_1\cup B_2 \cup … \cup B_n = S.\)

1-6.贝叶斯公式

\[P(B_i|A)=\frac{P(B_iA)}{P(A)}=\frac{P(A|B_i)P(B_i)}{\sum\limits_{j=1}^n{P(A|B_j)P(B_j)}},i=1,2…n. \]

其中，\(P(A)>0,P(B_i)>0(i=1,2…n)\)

1-7.先验概率与后验概率

先验概率：\(P(Y)\)
后验概率：\(P(Y|X)\)
先验概率是事前概率，是历史数据统计得到的预判概率；后验概率是一个事件发生后另外一个事件发生的概率，是条件概率。
举例：
根据历史统计数据，这个季节下雨的概率为\(P(A)\)，而打雷后下雨的概率为\(P(A|B)\)，前者为先验概率，后者为后验概率。
贝叶斯公式就是一种通过先验概率计算后验概率的方法。

1-8.独立事件

相互独立：
设A、B是两个随机事件，如果满足\(P(AB)=P(A)P(B)\)，则称A、B相互独立。
定理1：
设A、B是两个随机事件，且\(P(A)>0\)，则A、B相互独立等价于\(P(B|A)=P(B)\)。
如果两个时间相互独立，那么一个事件是否发生对另一个事件发生没有影响。
定理2：
如果A、B相互独立，则\(\bar A\)与\(B\)、\(\bar A\)与\(\bar B\)、\(A\)与\(\bar B\)均为相互独立事件。
推广到n个事件：
设\(A_1,A_2,……,A_n\)是\(n(n \geq 2)\)个事件，如果其中任意多个事件的积事件的概率，都等于各事件的概率之积，则称\(A_1,A_2,……,A_n\)相互独立。

---

Part2. 随机变量

2-1.随机变量

随机试验可能的结果形成了样本空间S，随机事件就是样本空间S的某个子集，而样本空间S中每个元素e都会对应一个实数，这种映射关系可以定义为一个函数f(e)，那么这个函数就c称为随机变量。
这样定义随机变量：随机变量是随机试验样本空间上的单值实数函数。
因此，随机变量的取值是由随机试验的结果确定，具有概率性。
举例：
重复的抛出一枚均匀的硬币，其结果可能是正面朝上，也可以能是反面朝上，结果可能情况提前知道但不确定具体是哪种结果，所以说，这是一个随机试验。
"结果正面朝上"是其中一种结果，是一个随机事件，可能发生，也可能不发生。
如果定义“抛出一枚硬币，正面朝上的次数”为X，那么，“结果正面朝上”时，X=1；“结果反面朝上”时，X=0。那么X就是一个随机变量。

2-2.连续型随机变量与离散型随机变量

离散型随机变量：取值可以一一列举，有限个或者可列举的无限多个。
连续型随机变量：取值不能一一列举，可能取值连续的充满了某一区间。

2-3.离散型随机变量的分布律

定义：设离散型随机变量\(X\)所有可能的取值为\(x_k(k=1,2,…)\)，X取各个可能值的概率为：

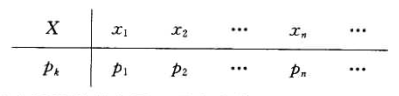
\[P\{X=x_k\}=p_k,k=1,2,… $$其中$p_k$满足两个条件：1）$p_k \geq 0,k=1,2…$；2）$\sum\limits_{k=1}^\infty{p_k}=1$。 可以将分布律用表格表示：  <br> ##2-4.随机变量的分布函数 定义：设X是一个随机变量，x是任意实数，函数: $$F(X)=P\{X \geq x\}, -\infty < x < +\infty $$ 称为$X$的**分布函数**。 有以下性质： 1）对于任意实数，$x_1,x_2(x_1 \leq x_2)$，有: \]

P{x_1< X \leq x_2}=P{X \leq x_2}-P{X \leq x_1}=F(x_2)-F(x_1)

\[2）$F(X)$是一个不减函数； 3）$F(-\infty)=0,F(+\infty)=0$； 4）$F(X)$是一个右连续函数； <br> ##2-5.连续型随机变量的概率密度函数 对于一个连续型随机变量$X$,其分布函数为$F(X)$，如果存在非负函数$f(x)$，并且对于任意实数$x$，有： \]

F(X)=\int_{-\infty}^x {f(t)}{\rm d}t

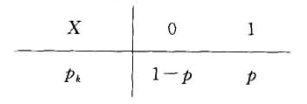
\[那么就称$f(x)$为随机变量$X$的**概率密度函数**。 有以下性质： 1）$f(x) \geq 0$； 2）$\int_{-\infty}^{+\infty} {f(x)}{\rm d}x=1$； 3）对于任意实数$x_1,x_2(x_1 \leq x_2)$，有$P\{x_1<X \leq x_2\}=F(x_2)-F(x_1)=\int_{x_1}^{x_2} {f(x)}{\rm d}x$； 4）若$f(x)$在点$x$处连续，则有$F'(X)=f(x)$。 <br> ##2-6.重要的随机变量分布 ###（1）0-1分布 **定义**：随机变量$X$只可能取两个值：0或者1，分布律为： \]

P{X=x_k}=p^k{(1-p){1-k}},k=0,1,其中0<p<1.

\[ ###（2）二项分布 **伯努利试验**：某一个试验只有两种可能的结果，独立的进行n次重复试验，称为**n重伯努利试验**。 两个特点：1）重复：两个可能的结果及其概率不变；2）独立：两两试验之间互不影响。 **定义**：随机变量$X$表示n重复伯努利试验中某事件A发生的次数，那么它的概率为： \]

P{X=k}={n \choose k}{p^k}{(1-p){n-k}},k=0,1,…,n

\[ 其中，$p$为事件A发生的概率。 我们称$X$服从(n,p)的**二项分布**，当n=1时，即为0-1分布。 ###（3）几何分布 **定义**：随机变量$X$表示n重复伯努利试验中某事件A第一次发生时的试验次数，那么它的概率为： \]

P{X=k}=(1-p)^{k-1}p,k=1,2,…

\[ 其中，$p$为事件A发生的概率。 我们称$X$服从**几何分布**，记为$X~G(p)$。 ###（4）泊松分布 **定义**：随机变量X所有可能取值为0,1,2,…，如果各个取值的概率为： \]

P{X=k}=\frac{\lambda ^k{e{-\lambda}}}{k!},\lambda > 0

\[ 则称随机变量$X$服从**泊松分布**，记为$X$~$\pi(\lambda)$。 ###（5）均匀分布 **定义**：如果连续型随机变量X具有概率密度函数： \]

f(x)=\begin{cases}
\frac{1}{b-a},\quad a \leq x\leq b\
0, \quad 其他
\end{cases}

\[则称$X$在区间$[a,b]$上服从**均匀分布**，记为$X$~$U(a,b)$。 均匀分布的概率大小只与区间长度有关，与区间位置无关。 ###（6）指数分布 **定义**：如果连续型随机变量X具有概率密度函数： \]

f(x)=\begin{cases}
\frac{1}{\theta}e^{-x/\theta},\quad x>0\
0, \quad 其他
\end{cases}

\[其中，$\theta>0$为常数，则称$X$服从参数为$\theta$的**指数分布**。 具有以下性质： 对于任意的$s,t>0$，有$P\{X>s+t|X>s\}=P\{X>t\}$ ###（7）正态分布 **定义**：如果连续型随机变量$X$的概率密度函数为： $$f(x)= \frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2{\sigma}^2}}, -\infty <x< +\infty $$ 其中$\mu,\sigma(\sigma>0)$为常数，则称X服从参数为$\mu,\sigma$的**正态分布（高斯分布**），记为$X$~$N(\mu,{\sigma}^2)$。 具有以下性质： 1）图像关于$x=\mu$轴对称，$x=\mu$取到最值$\frac{1}{\sqrt{2\pi}\sigma}$； 2）$\sigma$越小，曲线越尖瘦，越大越矮胖。 其分布函数为： \]

F(X)=\frac{1}{\sqrt{2\pi}\sigma} \int_{-\infty}^xe{-\frac{(t-\mu)^2}{2{\sigma}2}}dt

\[**标准正态分布**： 当$\mu=0,\sigma=1$时，随机变量X服从**标准正态分布**。 其概率密度函数为： \]

f(x)=\frac{1}{\sqrt{2\pi}}e^{-\frac{x2}{2}}, -\infty <x< +\infty

\[其分布函数为： \]

F(X)=\frac{1}{\sqrt{2\pi}} \int_{-\infty}^xe{2}}dt

\[普通正态分布函数转为标准正态分布函数： \]

F(X)=\Phi(\frac{X-\mu}{\sigma})

\[**$3\sigma$原则**： 如果一个随机变量服从正态分布$N(\mu,{\sigma}^2)$，那么其99.74%的概率会分布在$(\mu-3\sigma,\mu+3\sigma)$范围内。 <br> <br> ---------- ##Part3. 随机变量的数学特征 ###3-1.期望 期望，又称均值，由随机变量$X$的概率分布确定。 对于一个离散型随机变量$X$，其分布律为$P\{X=x_k\}=p_k,k=1,2,…$，则其期望为： \]

E(X)=\sum_{k=1}^{+\infty}{x_k}{p_k}

\[对于一个连续型随机变量$X$，其概率密度函数为$f(x)$，则其期望为： \]

E(X)=\int_{-\infty}^{+\infty} x{f(x)}dx

\[期望的性质： 1）设$C$为常数，则有$E(C)=C$； 2）设$X$是一个随机变量，C是常数，则有$E(CX)=CE(X)$； 3）设$X,Y$是两个随机变量，则有$E(X+Y)=E(X)+E(Y)$，可推广到任意有限个随机变量之和； 4）设$X,Y$是相互独立的随机变量，则有$E(XY)=E(X)E(Y)$，可推广到任意有限个相互独立的随机变量之积。 <br> ###3-2.方差 方差，用来度量随机变量X与其均值E(X)之间的偏离程度。D(X)越小代表数据越集中，越大代表数据越分散。 \]

D(X)=Var(X)=E{[X-E(X)]^2}

\[标准差，或称均方差为$\sigma(X)=\sqrt{D(X)}$。 对于一个离散型随机变量，其方差为： \]

D(X)=\sum_{k=1}^{{+\infty}{[x_k-E(X)]}2{p_k}}

\[对于一个连续型随机变量，其方差为： \]

D(X)=\int_{-\infty}^{+\infty} {[x-E(X)]^2}{f(x)}dx

\[另外，方差与期望之间有如下关系： \]

D(X)=E(X^2)-[E(X)]2

\[方差的性质： 1）设$C$为常数，则$D(C)=0$； 2）设$X$施随机变量，$C$是常数，则有：$D(CX)=C^2{D(X)}, D(X+C)=D(X)$ 3）设$X,Y$是两个随机变量，则有$D(X+Y)=D(X)+D(Y)+2E\{(X-E(X))(Y-E(Y))\}$ 特别地，如果$X,Y$相互独立，则有$D(X+Y)=D(X)+D(Y)$。 <br> ###3-3.协方差与相关系数 二维随机变量$(X,Y)$，定义随机变量$X$与$Y$的**协方差**： \]

Cov(X,Y)=E{[X-E(X)][Y-E(Y)]}

\[ 有以下性质： 1）$Cov(X,Y)=Cov(Y,X)$ 2）$Cov(X,X)=D(X)$ 3）$D(X+Y)=D(X)+D(Y)+2Cov(X,Y)$ 4）$Cov(X,Y)=E(XY)-E(X)E(Y)$ 5）$Cov(aX,bY)=abCov(X,Y),a,b$是常数 6）$Cov(X_1+X_2,Y)=Cov(X_1,Y)+Cov(X_1,Y)$ 定义随机变量X与Y的**相关系数**： \]

\rho_{XY}=\frac{Cov(X,Y)}{\sqrt{D(X)}\sqrt{D(Y)}}

\[ 有以下性质：$|\rho_{XY}| \leq 1$ $\rho_{XY}$是一个可以用来表征$X,Y$之间线性关系紧密程度的量。当$|\rho_{XY}|$较大时，就认为$X,Y$线性相关程度大；$|\rho_{XY}|$较小时，就认为$X,Y$线性相关程度小；$|\rho_{XY}|$为0时，就认为$X,Y$不相关；$|\rho_{XY}|$为1时，就认为$X,Y$完全线性相关。 $X,Y$相互独立时，一定不相关；$X,Y$不相关时，则不一定相互独立。 <br> ###3-4.原点矩与中心矩 设$X,Y$是随机变量， k阶原点矩：$E(X^k),k=1,2,…$ k阶中心矩：$E([X-E(X)]^k),k=2,3,…$ k+l阶混合矩：$E({X^k}{Y^l}),k,l=1,2,…$ k+l阶混合中心矩：$E({[X-E(X)]^k}{[Y-E(Y)]^l}),k,l=1,2,…$ 可以看出：期望E(X)是一阶原点矩，方差D(X)是而阶中心距，协方差Cov(X,Y)是X和Y的二阶混合中心矩。 <br> ###3-5.协方差矩阵 对于二维随机变量$(X_1,X_2)$，如果它的四个二阶中心矩都存在，记为： $c_{11}=E\{[X_1-E(X_1)]^2\}$ $c_{12}=E\{[X_1-E(X_1)][X_2-E(X_2)]\}$ $c_{21}=E\{[X_2-E(X_2)][X_1-E(X_1)]\}$ $c_{22}=E\{[X_2-E(X_2)]^2\}$ 将它们排成矩阵形式： \]

\begin{pmatrix} c_{11} & c_{12}\ c_{21} & c_{22} \ \end{pmatrix}

\[这个矩阵就是随机变量$(X_1,X_2)$的协方差矩阵。 推广到$n$维随机变量$(X_1,X_2,…,X_n)$的二阶混合中心矩，如果： $c_{ij}=Cov(X_i,Y_j)=E\{[X_i-E(X_i)][X_j-E(X_j)]\},i,j=1,2,…$ 都存在，则称矩阵： \]

\begin{pmatrix}
\begin{array}{cccc}
c_{11} & c_{12} & \dots & c_{1n}\
c_{21} & c_{22} & \dots & c_{2n}\
\vdots & \vdots & &\vdots\
c_{n1} & c_{n2} & \dots & c_{nn}\
\end{array}
\end{pmatrix}

\[ 为$n$维随机变量$(X_1,X_2,…,X_n)$的协方差矩阵。 <br> ###3-5.重要分布的数学特征 0-1分布：期望$p$、方差$p(1-p)$ 二项分布：期望$np$、方差$np(1-p)$ 几何分布：期望$\frac{1}{p}$、方差$\frac{1-p}{p^2}$ 泊松分布：期望$\lambda$、方差$\lambda$ 均匀分布：期望$\frac{a+b}{2}$、方差$\frac{(b-a)^2}{12}$ 指数分布：期望$\theta$、方差${\theta}^2$ 正态分布：期望$\mu$、方差${\sigma}^2$ <br> <br>\]