数据准备<4>:变量筛选-理论篇

在上一篇文章《数据准备<3>：数据预处理》中，我们提到降维主要包括两种方式：基于特征选择的降维和基于维度转换的降维，其中基于特征选择的降维通俗的讲就是特征筛选或者变量筛选，是指从多个特征（变量）中筛选出显著的特征（变量），在分类预测问题中，就是筛选出对目标变量有预测能力的特征（变量）。本篇主要介绍特征（变量）筛选的基本思路与方法，为简洁，下文均使用“变量筛选”指代。

变量筛选主要有三种方法：基于经验的方法（比如专家法）、基于统计的方法（比如信息增益、区分度）和基于机器学习的方法（比如决策树算法）。下面将分别具体介绍：

1.基于经验的方法

根据业务专家或者数据专家的以往经验、实际数据情况、业务理解程度等进行综合考虑。业务专家依靠的是业务背景，从众多维度变量中选择对结果影响较大的变量；而数据专家依靠的则是数据工作经验，基于数据的基本特征以及对后期数据处理和建模的影响来选择或者排除，比如删除缺失值较多的变量。

2.基于统计的方法

构建统计指标，对变量的预测能力进行度量，选择其中预测能力较大的变量。
首先，从香农的信息熵说起。
香农（Claude Elwood Shannon，1916年4月30日—2001年2月24日）是美国数学家、信息论的创始人，他在1948年发表的《通信的数学理论》论文中提出了信息熵的概念，认为信息是用来减少随机不确定的东西，使用信息熵对信息进行定量度量。
定义任意一个随机事件\(X\)，其发生的可能情况有\(x_1,x_2……,x_n\)，对应的概率分别为\(p_1,p_2,……,p_n\)，它的信息熵\(H(X)\)定义为：

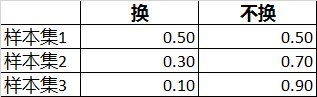
\[H(X)=-\sum_{i=1}^n{p_i*log(p_i)} $$信息熵反映了消除这个随机事件不确定性所需要的信息量的大小，换言之，信息熵度量了一个随机事件不确定程度的大小。 信息熵越大，代表一个随机事件不确定程度越高，消除这个随机事件不确定性所需要的信息就越多。 **例1：**现在要基于历史样本集预测一个新用户是否会换机，提供了三个样本集：  对于一个用户来说，是否会换机是一个随机事件，其取值有两种情况：换、不换。 在三个样本集下，该随机事件的概率分布分别为：  对应的，在三个样本集下，这个随机事件的信息熵分别为： 样本集1：H=1 样本集2：H=0.88 样本集3：H=0.47 可以看到，随机事件的概率分布越均匀，它的不确定程度就越大，信息熵就越大。 下面我们回到变量筛选的话题中。 **变量筛选是筛选出对目标变量的预测有帮助的变量，那么又如何定义一个变量对目标变量的预测有帮助？** 可以认为，如果引入一个变量后，这个变量能够一定程度上消除目标变量这个随机事件的不确定性，那么就说这个变量对目标变量的预测有帮助，换言之，这个变量具有对目标变量的预测能力。如果消除不确定性的程度越大，那么这个变量就越重要、预测能力就越强。 明白这一点后，事情就变得简单起来。我们可以通过评估引入某个变量前后，目标变量这个随机事件的不确定性的变化大小，来度量一个变量对目标变量的预测能力强弱。 ### 2.1 信息增益 信息增益的概念非常简单，就是引入一个变量前后，一个随机事件的信息熵的变化值，通俗的说，就是不确定性消除的大小。 \]

Gain(A) = H(X) - H(X,A)

\[其中，$H(X)$为引入变量A之前随机事件X的信息熵，$H(X,A)$为引入变量A之后随机事件X的信息熵。 显然，信息增益越大，代表引入变量A之后，消除随机事件X不确定性的程度越大，说明变量A对目标变量X的预测能力就越强。 另外，我们称$H(X,A)$为条件熵，即随机变量X在条件A下的信息熵。其计算方法为： \]

H(X,A)=-\sum_{j=1}^{m{pa_j}\sum_{i=1}}n{(p_i|pa_j)*log(p_i|pa_j)}

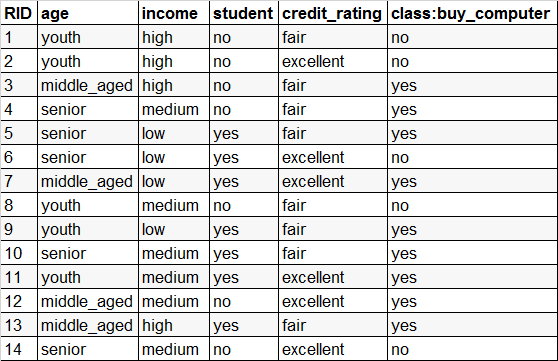
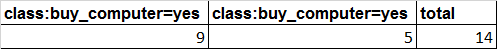
\[其中，$p_i|pa_j$为条件A取值为j的情况下随机变量X的取值概率，$pa_j$为随机变量A取值为j的概率。 **例2：**使用经典的AllElectronics数据集，用于预测一个顾客是否会购买电脑。  从样本总体上看：  如果引入age变量，如下：  如果引入income变量，如下：  可以得到： H(X)=0.9403 H(X,'age')=0.6935，Gain(X,'age')=0.2468 H(X,'income')=0.9111，Gain(X,'income')=0.0292 由于Gain(X,'age')>Gain(X,'income')，所以变量age比变量income对目标变量buy_computer的预测能力要强。 ### 2.2 基尼指数 基尼指数（Gini Index），是另一个用来度量随机事件不确定程度的指标，其定义**Gini(X)**为： \]

Gini(X)=\sum_{i=1}^{n{p_i*(1-p_i)}=1-\sum_{i=1}}n{p_i^2}

\[针对例1，分别计算基尼指数： 情况1：Gini=0.50 情况2：Gini=0.42 情况3：Gini=0.18 可以看出，基尼指数越大，随机事件的不确定程度就越大。 类似于信息增益的定义，定义指标“基尼指数降低值”： \]

\Delta{Gini}(A) = Gini(X) - Gini(X,A)

\[其中，$Gini(X)$为引入变量A之前随机事件X的基尼指数，$Gini(X,A)$为引入变量A之后随机事件X的基尼指数。$Gini(X,A)$的计算方法如下： \]

Gini(X,A)=\sum_{j=1}^{m{pa_j}\sum_{i=1}}n{(p_i|pa_j*(1-p_i|pa_j))}=\sum_{j=1}^{m{pa_j}\sum_{i=1}}n{(1-(p_i|pa_j)^2)}

\[其中，$p_i|pa_j$为条件A取值为j的情况下随机变量X的取值概率，$pa_j$为随机变量A取值为j的概率。 同样，基尼指数降低值越大，代表引入变量A之后，消除随机事件X不确定程度越大，说明变量A对目标变量X的预测能力就越强。 针对例2，计算基尼指数及其降低值： Gini(X)=0.4592 Gini(X,'age')=0.3429，$\Delta$Gini('age')=0.1163 Gini(X,'income')=0.4405，$\Delta$Gini('income')=0.0187 $\Delta$Gini('age')>$\Delta$Gini('income')，因此变量“age”比变量“income”对目标变量的预测能力要强。 ### 2.3 区分度 在二分类问题中，可以使用区分度这个指标，它是从另一个角度来评估随机事件不确定程度的指标。 上文中，信息增益和基尼指数降低值，都是从引入变量A后随机事件X不确定性的消除程度来评估变量A对X的预测能力的。由于引入变量A前，随机事件X的不确定程度是确定的，消除程度越大，说明引入变量A后随机事件X的不确定程度越小，所以也可以直接通过度量引入变量A后随机事件X的不确定程度来评估变量A对X的预测能力。区分度正是这样的指标。 在上文中，我们还知道，随机事件的概率分布越均匀，它的不确定程度越大。 因此，基于这两点，定义“区分度”如下： \]

区分度=max_{j=1}^m(pa_j/p)

\[其中，$p$为引入变量A以前随机变量X取值为响应值的概率，$pa_j$为引入变量A之后，在变量A取值为j时，随机变量X取值为响应值的概率。 区分度反映了引入变量A后随机事件X发生概率的均匀程度，取值越大，代表越不均匀，不确定程度就越小，变量A的预测能力就越强。 针对例2，它属于一个二分类问题，buy_computer='yes'为响应值。 区分度('age')=1.56 区分度('income')=1.17 区分度('age')>区分度('income')，因此变量“age”比变量“income”对目标变量的预测能力要强。 **一般的，将区分度=1.5作为筛选阈值，选择区分度大于1.5的变量。** 另外，如果变量A为连续型时，计算前需要对其进行离散化处理。 ### 2.4 信息值（IV） 在二分类问题中，也可以使用信息值（Information Value，IV）度量变量A对随机事件X的预测能力。 定义如下： \]

woe_j=ln(\frac{{cov_Y}_j}{{cov_N}_j})=ln(\frac{\frac{Y_j}{Y}}{\frac{N_j}{N}})

\[\]

IV=\sum_{j=1}^{m{({cov_Y}_j-{cov_N}_j)*woe_j}=\sum_{j=1}}m{({\frac{Y_j}{Y}}-{\frac{N_j}{N}})*woe_j}

\[其中，woe（Weight of Evidence，证据权重），它是根据变量A的取值将随机事件样本集进行分组，分成m组，每组分别计算woe取值。 woe等于每一组内响应样本的覆盖率（${cov_Y}_j$）与非响应样本的覆盖率（${cov_N}_j$）的比值的取对数，从这个定义上可以理解成，woe考察的是每个分组内，响应样本相对非响应样本的分布差异，如果二者没有差异，说明与总体分布完全相同，此时woe取值为0。当响应样本分布多于非响应样本，woe>0；反之，woe<0。 由于woe的取值有正有负，同时，衡量变量A的预测能力是一个样本全集概念，而不是某一个样本子集，因此，将每一组内响应样本的覆盖率与非响应样本的覆盖率的差值作为权重，对woe进行加权求和得到的值，定义为IV，既可以得到一个整体指标，也可以将指标值调和成正值。 针对例2，buy_computer='yes'为响应值，buy_computer='no'为非响应值。 IV('age')=2.0358 IV('income')=0.1773 IV('age')>IV('income')，因此变量“age”比变量“income”对目标变量的预测能力要强。 **一般的：**  **将0.10作为筛选阈值，选择IV大于等于0.10的变量。** 需要说明的：关于**分组中的响应值或者非响应值为0**时的处理方式： 1）重新分组，尽量不出现这种情况； 2）手工调整这个值，将其调整为1。 和区分度计算相同，如果变量A为连续型时，计算IV前需要对其进行离散化处理。 <br> ## 3.基于机器学习的方法 基于机器学习的方法进行变量筛选，是指构建一个或者多个机器学习模型，来判断每个变量的重要程度，得到最重要的变量。与基于统计的方法相比，基于机器学习的方法同时考虑了所有变量，而不是对单个变量进行独立度量。 ### 3.1 单一模型 基于单一模型的方法，是指构建一个有监督的机器学习模型，这个模型不需要用于最终的模型构建，模型自动为每个变量提供某种重要性度量，进而通过这个度量进行重要性排序，比如使用决策树、随机森林等，算法内部包含有变量重要性度量指标。 ### 3.2 迭代 基于迭代的方法，其实就是基于多个模型甚至是一系列模型来进行判断。它主要有两种思路：前向筛选和后向筛选，即开始时没有变量，然后逐个添加变量，直到满足某个终止条件；或者从所有变量开始，然后逐个删除变量，直到满足某个终止条件。 **由于涉及到具体的实现环境，这一部分将在下一篇[《数据准备<5>:变量筛选-实战篇》](https://www.cnblogs.com/hbsygfz/p/9255112.html)结合sklearn环境进行具体介绍。** <br> ## 4. 参考与感谢 \[1] [数据挖掘概念与技术](https://book.douban.com/subject/2038599/) \[2] [Python机器学习基础教程](https://book.douban.com/subject/30147778/) \[3] [Python数据分析与数据化运营](https://book.douban.com/subject/27608466/) \[4] [百度百科:香农](https://baike.baidu.com/item/%E5%85%8B%E5%8A%B3%E5%BE%B7%C2%B7%E8%89%BE%E5%B0%94%E4%BC%8D%E5%BE%B7%C2%B7%E9%A6%99%E5%86%9C/10588593?fromtitle=%E9%A6%99%E5%86%9C&fromid=1146248&fr=aladdin) <br> <br>\]