2023牛客寒假算法基础集训营1
2023牛客寒假算法基础集训营1
特别说明:本篇题解代码借鉴了jiangly大佬的AK代码和牛客出题人的思路
官方题目难度排名
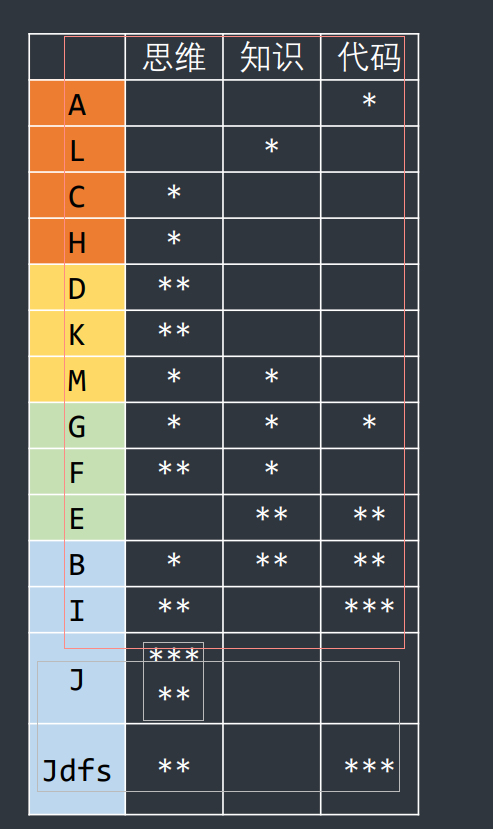
再一次说明:本题解只涉及前三难度等级的题目,B题I题J题水平达不到,没有涉及
A.World Final? World Cup! (I)
题目描述
思路点拨
前后缀的思路,代码一看便能理解
提交代码
#include<bits/stdc++.h>
void solve()
{
std::string s;
std::cin >> s;
int res[] = {5,5};
int score[] = {0,0};
for(int i=0;i<10;i++)
{
int x = i % 2;
res[x]--;
score[x] += s[i] - '0';
if(res[1] + score[1] < score[0] ||res[0] + score[0] < score[1])
{
std::cout << i + 1 << "\n";
return;
}
}
std::cout << -1 << "\n";
}
int main()
{
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
int t;std::cin>>t;
while(t--)
{
solve();
}
return 0;
}
C.现在是,学术时间 (I)
题目描述
思路点拨
- 简单贪心
- 总的H指数会受教授数影响,根据题目定义,首先想到的是让几个人的文章交给一个人去发,但是你要明白一个人就有一篇文章,如果每个人单独发自己的,最少会有引用量大于0的文章的数目大小的H指数,但是如果你多个人的文章交给某一个去发,最多会有这多个人+这一个人的数目大小的H指数,这还必须保证这多个人的每个人的引用量都大于等于这多个人+这一个人的人数数目,所以贪心考虑,直接每个人发自己的文章,只要每个人的引用量大于零,便可以+1。
提交代码
#include<bits/stdc++.h>
using namespace std;
void solve()
{
int n;cin >> n;
vector<int> a(n);
int ans = 0;
for (int i=0;i<n;i++)
{
cin >> a[i];
if(a[i] > 0) ans ++;
}
cout << ans << "\n";
return;
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(nullptr);
int t;cin >> t;
while(t--)
{
solve();
}
return 0;
}
D.现在是,学术时间 (II)
题目描述
思路点拨

不好证明,但是可以猜结论,猜另外一点肯定是A,B,C,D中其中一点,然后枚举四个点取最大的。
注意利用cout的保留小数代码
std::cout << std::fixed << std::setprecision(10) << "\n";
提交代码
#include<bits/stdc++.h>
void solve()
{
int x, y, a, b;
std::cin >> x >> y >> a >> b;
double ans = 0;
for(auto c:{0,x})
{
for(auto d:{0,y})
{
int xl = std::min(a, c);
int yl = std::min(b, d);
int xr = std::min(x, std::max(a, c));
int yr = std::min(y, std::max(b, d));
int inter = (xr-xl)*(yr-yl);
int uni = x * y + std::abs(a - c) * std::abs(b - d) - inter;
double res = 1. * inter / uni;
ans = std::max(ans, res);
}
}
std::cout << ans << "\n";
}
int main()
{
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
std::cout << std::fixed << std::setprecision(10) << "\n";
int t;
std::cin >> t;
while(t--)
{
solve();
}
return 0;
}
E.鸡算几何
题目描述
思路点拨
判断第三个操作是否一定用过,利用叉积,第三个操作会改变方向,也就是改变叉积,第一个操作和第二个操作不会改变方向
利用叉积,必须重写结构体(向量减法,必须要同时x和y减),注意这里还需要计算距离,也就是计算点积,判断AB长度和BC长度是否相同。
有一个坑点,ABC和DEF不对应,但是可以利用叉积选择都大于0或者都小于0的任意一边比较,如果用过第三个命令,说明比较的两条直线不相等,对于一种特殊情况也可以包括,如果AB和BC长度相同也可以判断出;当然如果没有用第三个命令,那么本身操作前后两个线就是一条线,长度自然相等。
提交代码
#include<bits/stdc++.h>
using i64 = long long;
using T = double;
struct Point
{
T x;
T y;
Point(T x = 0, T y = 0):x(x),y(y){}
Point & operator -= (Point &lhs)
{
x -= lhs.x, y -= lhs.y;
return *this;
}
friend Point operator - (Point lhs,Point &rhs)
{
return lhs -= rhs;
}
};
T dot(const Point &a ,const Point &b)
{
return a.x * b.x + a.y * b.y;
}
T cross(const Point &a,const Point &b)
{
return a.x * b.y - a.y * b.x;
}
void solve()
{
Point a[6];
for(int i = 0; i < 6; i++)
{
std::cin >> a[i].x >> a[i].y;
}
if(cross(a[0] - a[1], a[2] - a[1]) > 0) std::swap(a[0], a[2]);
if(cross(a[3] - a[4], a[5] - a[4]) > 0) std::swap(a[3], a[5]);
double len0 = std::sqrt(dot(a[0] - a[1], a[0] - a[1]));
double len1 = std::sqrt(dot(a[3] - a[4], a[3] - a[4]));
if(std::abs(len0 - len1) >= 1e-9) puts("YES");
else puts("NO");
return ;
}
int main()
{
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
int t;
std::cin >> t;
while(t--)
{
solve();
}
return 0;
}
F.鸡玩炸蛋人
题目描述
思路点拨
- 联通块,利用并查集DSU

提交代码(DSU板子,借鉴jiangly大佬的)
#include<bits/stdc++.h>
using i64 = long long;
struct DSU
{
std::vector<int> f,siz;
DSU(int n) :f(n),siz(n,1){std::iota(f.begin(), f.end(), 0);}
int leader(int x)
{
while(x != f[x]) x = f[x] = f[f[x]];
return x;
}
bool same(int a,int b)
{
return leader(a) == leader(b);
}
bool merge(int a, int b)
{
a = leader(a);
b = leader(b);
if(a == b) return false;
siz[a] += siz[b];
f[b] = a;
return true;
}
int size(int a)
{
return siz[leader(a)];
}
};
int main()
{
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
int n, m;
std::cin >> n >> m;
DSU dsu(n);
for(int i = 0; i < m ; i++)
{
int u,v;
std::cin >> u >> v;
u--,v--;
dsu.merge(u,v);
}
int comp = 0;
std::vector<int> s(n,0);
for(int i = 0; i < n;i++)
{
int c;
std::cin >> c;
if(c)
{
int x = dsu.leader(i);
comp += !s[x];
s[x] += c;
}
}
i64 ans = 0;
for(int i = 0; i < n; i++)
{
if(dsu.leader(i) == i)
{
if(comp - (s[i] > 0) == 0)
{
int s = dsu.size(i);
ans += 1ll * s * s;
}
}
}
std::cout << ans << "\n";
return 0;
}
G.鸡格线
题目描述
思路点拨
- 维护到叶子结点的线段树,不需要懒标记
- 对于\(f(x) = round(10\sqrt x )\)来说,0,100,99得到的结果是循环的,所以这三个情况需要特殊处理,注意这里的线段树需要存储一个区间段的最大最小值,只为判断一个区间的范围在99~100之间就可以不用操作,减少时间浪费。
提交代码
#include<bits/stdc++.h>
using i64 = long long;
constexpr int N = 1 << 18;
i64 sum[N];
int max[N], min[N];
void pull(int o)
{
max[o] = std::max(max[2 * o], max[2 * o + 1]);
min[o] = std::min(min[2 * o], min[2 * o + 1]);
sum[o] = sum[2 * o] + sum[2 * o + 1];
}
void build_tree(int o, int l, int r, auto &a)
{
if(r - l == 1)
{
max[o] = min[o] = sum[o] = a[l];
if(!a[l]) max[o] = 100, min[o] = 100;
return;
}
int mid = ( l + r ) >> 1;
build_tree(2 * o, l, mid, a);
build_tree(2 * o + 1, mid, r, a);
pull(o);
}
void modify(int o, int l, int r, int x, int y, int k)
{
if(max[o] <= 100 && min[o] >= 99) return;
if(l >= y|| x >= r) return ;
if(r - l == 1)
{
while(k && max[o] != 100 && max[o] != 99)
{
k--;
max[o] = std::sqrt(max[o]) * 10 + .5;
}
min[o] = sum[o] = max[o];
return ;
}
int mid = (l + r) >> 1;
modify(2 * o, l, mid, x, y, k);
modify(2 * o + 1, mid, r, x, y, k);
pull(o);
}
int main()
{
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
int n, m;
std::cin >> n >> m;
std::vector<int> a(n);
for(int i = 0; i < n; i++)
{
std::cin >> a[i];
}
build_tree(1,0,n,a);
while(m--)
{
int op;
std::cin >> op;
if(op == 1)
{
int l, r, k;
std::cin >> l >> r >> k;
l--;
modify(1,0,n,l,r,k);
}
else
{
std::cout << sum[1] << "\n";
}
}
return 0;
}
H.本题主要考察了DFS
题目描述
思路点拨
诈骗,不用求出对应那个是题目中的“1”标签,还是“2”标签,只问你最后一块的成本,用整个大的减去剩余块的成本就是答案
提交代码
#include<bits/stdc++.h>
void solve()
{
int n;
std::cin >> n;
int sum = 0;
for(int i = 0; i < n * n - 1; i++)
{
std::string s;
std::cin >> s;
sum += 10;
for(int i = 0; i < 4;i++)
{
if(s[i] == '1') sum--;
if(s[i] == '2') sum++;
}
}
int total = 10 * n * n;
std::cout << total - sum << "\n";
return ;
}
int main()
{
int t;
std::cin >> t;
while(t--)
{
solve();
}
return 0;
}
K.本题主要考察了dp
题目描述
思路点拨
-
法一:利用动态规划(推荐,训练思维)
-
\(dp[j][x][y]\)表示状态,j是指当前枚举到第几个1了,x和y分别指当今序列后两位代表的数字,注意原本应该为四维,第一维度为当前选择的第几个,但是可以省去这一维,但是必须存储上一层的状态,利用辅助三维数组\(g[j][x][y]\)。
-
$g[j+z][y][z] =min(g[j+z][y][z],dp[j][x][y] + 0) $ \(i<2时,\)
-
$g[j+z][y][z] =min(g[j+z][y][z],dp[j][x][y] + (x+y+z>=2) $ \(i>=2时\)
-
最后答案是\(dp[m][0][0],dp[m][0][1],dp[m][1][0],dp[m][1][1]\)中最小的一个。
-
i>=2才可转移,原因是最少需要有三位,根据题意,这里i从0开始计数。
-
利用的c++语法,构造三维数组,并且所有的数赋值为\(\infty\),即INF:
-
单独赋值用法 int m = 19; std::vector dp(m+1, std::array<std::array<int,3>,3>{1,2,3,4,5,6,7,8,9}); std::cout << dp[11][0][0] <<" "; std::cout << dp[18][0][1] <<" "; std::cout << dp[19][0][2] <<" "; std::cout << dp[10][1][0] <<" "; std::cout << dp[13][1][1] <<" "; std::cout << dp[15][1][2] <<" "; std::cout << dp[12][2][0] <<" "; std::cout << dp[17][2][1] <<" "; std::cout << dp[14][2][2] <<"\n"; -
法二:贪心构造
-
考虑1001001001001……肯定是构造的最少的具有坏区间的序列,多余的1放到后面
-
存在如下情况
-
- 对于低于2位的串,n%3 == m,或者n<=2
-
- 答案为0
- 以100100……结尾或者000……结尾或者以1001结尾的,n/3 >= m-1
-
- 答案为0
- 以1001111……结尾,注意这里不包括1001结尾的,
-
- 答案为\(m-\dfrac{n-m}{2}-2+1\)
- 注意011算是1个坏区间,注意这里不包括1001结尾的,不能构成一个坏区间,不满足如上公式,
- 以1001011111……结尾
-
- 答案为\(m-\dfrac{n-m}{2}-1-2+2\)
- 直接都是全1串,n==m ,
-
- 答案为n-2
-
统一来说
-
n==m时,ans = n-2;
-
n%3==m || n/3>=m-1 ,ans = 0;
-
其他,ans = \(m-\dfrac{n-m}{2}-1\)
提交代码
- 法一:动态规划
#include<bits/stdc++.h>
constexpr int INF = 1e9;
void solve()
{
int n,m;
std::cin >> n >> m;
std::vector dp(m+1,std::array<std::array<int,2>,2 >{INF,INF,INF,INF});
dp[0][0][0] = 0;
for(int i = 0; i < n; i++)
{
std::vector g(m+1,std::array<std::array<int,2>,2 >{INF,INF,INF,INF});
for(int j = 0; j <= m; j++)
{
for(auto x:{0,1})
{
for(auto y:{0,1})
{
for(auto z:{0,1})
{
if(j+z > m) continue;
int &res = g[j+z][y][z];
res = std::min(res, dp[j][x][y] + (i>=2 && x + y + z >= 2));
}
}
}
}
std::swap(dp,g);
}
int ans = INF;
for(auto x:{0,1})
{
for(auto y:{0,1})
{
ans = std::min(ans,dp[m][x][y]);
}
}
std::cout << ans << "\n";
}
int main()
{
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
int t = 1;
while(t--)
{
solve();
}
return 0;
}
- 法二:贪心构造
#include<bits/stdc++.h>
int main()
{
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
int n, m;
std::cin >> n >> m;
if(n==m) std::cout << n-2 << "\n";
else if(n <= 2 || n/3 >= m - 1) std::cout << 0 << "\n";
else std::cout<<m-(n-m)/2-1 << "\n";
return 0;
}
L.本题主要考察了运气
题目描述
思路点拨
- 方法1就是wa31发
- 方法2可以通过期望计算得到

- 注意计算的是次数的期望
公式为:x*p相加即可 - 具体计算公式如下:
- \(5.05-3.55 = 1.6\) , \(\dfrac{1.6}{5}=32\)
提交代码
#include<bits/stdc++.h>
using namespace std;
int main()
{
cout<<32<<"\n";
return 0;
}
M.本题主要考察了找规律
题目描述
思路点拨
转移方程:
\(dp[j - k] = max(dp[j - k] ,dp[j]+1.*k/j)\); 第一维就是当前多少个仙贝,直到所有仙贝都用完了
答案为\(dp[0]\)
提交代码
#include<bits/stdc++.h>
int main()
{
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
int n,m;
std::cin >> n >>m;
std::vector<int> dp(n+1);
for(int i = 0; i < n; i++)
{
for(int j = 0; j < m; j++)
{
for(int k = 1; k <= j; k++)
{
dp[j - k] = max(dp[j - k],dp[j] + 1. * k / j);
}
}
}
std::cout << fixed << setprecision(10) << dp[0] << "\n";
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号