树状数组
树状数组
一、适用范围
- 树状数组是一个查询和修改复杂度都为 \(log(n)\) 的数据结构,常常用于查询任意区间的所有元素之和。
- 与前缀和的区别是支持动态修改, \(log(n)\) 的时间进行修改,\(log(n)\) 查询。
- 支持如下操作:
- 单点修改区间查询
- 区间修改单点查询
- 区间修改区间查询
二、算法原理
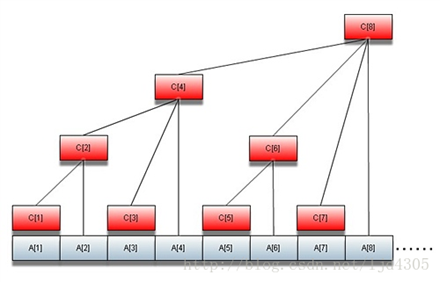
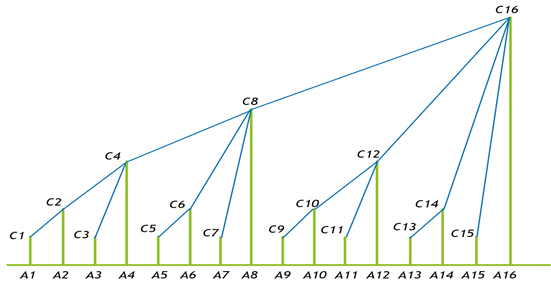
- 树状数组较好的利用了二进制。它的每个节点的值代表的是自己和前面一些连续元素的和。至于到底是前面哪些元素,这就由这个节点的下标决定。

- 设节点的编号为 \(i\) ,那么:
-
即可以推导出:
C[1] = A[1] # lowbit(1)个元素之和 C[2] = C[1] + A[2] = A[1] + A[2] # lowbit(2)个元素之和 C[3] = A[3] # lowbit(3)个元素之和 C[4] = C[2] + C[3] +A[4] = A[1] + A[2] + A[3] + A[4] # lowbit(4)个元素之和 C[5] = A[5] C[6] = C[5] + A[6] = A[5] + A[6] C[7] = A[7] C[8] = C[4] + C[6] + C[7] + A[8] = A[1] + A[2] + A[3] + A[4] + A[5] + A[6] + A[7] + A[8] -
显然一个节点并不一定是代表自己前面所有元素的和。只有满足 \(2^n\) 这样的数才代表自己前面所有元素的和。
-
理解 \(lowbit\) 函数
-
原码:如果机器字长为 \(n\),那么一个数的原码就是用一个 \(n\) 位的二进制数,其中最高位为符号位:正数为 \(0\),负数为 \(1\)。剩下的 \(n-1\) 位表示该数的绝对值。
-
反码:知道了原码,那么你只需要具备区分 \(0\) 跟 \(1\) 的能力就可以轻松求出反码,为什么呢?因为反码就是在原码的基础上,符号位不变其他位按位取反(就是 \(0\) 变 \(1\),\(1\) 变 \(0\))就可以了。
-
补码也非常的简单,就是在反码的基础上按照正常的加法运算加 \(1\) 。正数的补码就是其本身。负数的补码是在其原码的基础上符号位不变,其余各位取反,最后 \(+1\),即取反 \(+1\)
-
$lowbit(x)=x&-x $ :表示截取 \(x\) 二进制最右边的 \(1\) 所表示的值,可以写成函数或宏定义
-
注意宏定义是括号,因为宏名只是起到一个替代作用,不加括号在运算时优先级会出问题
//1. 宏定义,注意括号,不建议这样写,容易产生歧义 #define lowbit(x) ((x) & -(x)) //2. 函数写法,推荐写法: int lowbit(int x){return x & -x;}
-
三、 树状数组的操作
-
\(update\) 更新操作
-
因为树状数组 \(c[x]\) 维护的是一个或若干个连续数之和,当我们修改了 \(a[x]\) 之后,\(x\sim n\) 前缀和均发生了变化,所以除了\(c[x]\) 需要修改之外 \(x\) 的祖先节点也必须修改而 \(x\) 的父亲节点为 \(x+lowbit(x)\),我们叫向上更新。
-
把序列中第 \(i\) 个数增加 \(x\),\(sum[i]\sim sum[n]\) 均增加了 \(x\) ,所以我们只需把这个增量往上更新即可。如果,把 \(a[i]\) 修改成 \(x\),则我们向上更新 \(a[i]\) 的增量:\(x-a[i]\)。
//1. a[id] 增加 x while写法 void updata(int id,int x){ while(id<=n){//向上更新,更新到n为止 c[id]+=x; id+=lowbit(id); } } //2. a[id] 修改成 x for写法 void updata(int id,int x){//或者传递参数是x=x-a[id],此时跟第一种写法一样 for(int i=id;i<=n;i+=lowbit(i)) c[i]+=x-a[id]; }
-
-
\(getsum\) 查询操作
-
因为树状数组维护的是一个能够动态修改的前缀和,所以可以在 \(log(n)\) 的效率下求出前 \(n\) 项和\(sum[i]\) 。
-
如果 \(i=2^j (j=0,1,..n)\), 此时最简单,显然有:\(sum[i]=c[i]\) ,如果 \(i\) 是其他的情况呢?
- \(sum[5]=c[5]+c[4]\ (4=5-lowbit(5))\)
- \(sum[15]=c[15]+c[14]+c[12]+c[8]\ (14=15-lowbit(15),12=14-lowbit(14),...)\)
-
显然,想要求出前 \(i\) 项前缀和 \(sum[i]\) ,只需沿着当前节点向下累加直到节点编号为 \(2^j\) 为止。我们叫向下求和。
int getsum(int id){ int tot=0; for(int i=id;i>0;i-=lowbit(i)) tot+=c[i]; return tot; }
-
四、求逆序对
-
算法思想
- 逆序对就是如果 \(i > j\ \&\&\ a[i] < a[j]\),这两个就算一对逆序对。其实也就是对于每个数而言,找找排在其前面有多少个比自己大的数。
- 我们用数组 \(c[i]\) 记录在数 \(i\) 之前出现的在 \([i-lowbit[i],i]\) 的数的个数。
- 所以我们只需要向下更新,向上求和来求出逆序对的个数了。
- 注意,我们维护的是序列数的数值的大小,所以序列元素值 $a[i]>0 $ ,且元素大小不宜太大,而且必须为整数。
-
$Code $
#include <bits/stdc++.h> const int maxn=1e6+5; int n,ans,a[maxn],c[maxn]; int lowbit(int x){return x & -x;} void modify(int i){ for(;i;i-=lowbit(i)) c[i]+=1; } int getsum(int i){ int tot=0; for(;i<=maxn;i+=lowbit(i)) tot+=c[i]; return tot; } void Solve(){ scanf("%d",&n); for(int i=1;i<=n;++i){ scanf("%d",&a[i]); a[i]++; //避免a[i]-1=0 ans+=getsum(a[i]-1); modify(a[i]); } printf("%d\n",ans); } int main(){ Solve(); return 0; } -
离散化版 \(Code\)
#include <bits/stdc++.h> const int maxn=1e5+5; int a[maxn],b[maxn],c[maxn]; int n,cnt; int lowbit(int x){return x & -x;} void updata(int i){ for(;i;i-=lowbit(i)) c[i]+=1; } int getsum(int i){ int tot=0; for(;i<=n;i+=lowbit(i)) tot+=c[i]; return tot; } void Solve(){ scanf("%d",&n); srand(time(0)); for(int i=1;i<=n;++i){ a[i]=rand()%n; b[i]=a[i]; printf("%d ",a[i]); } printf("\n"); std::sort(b+1,b+n+1); cnt=std::unique(b+1,b+n+1)-b; for(int i=1;i<=n;++i) a[i]=std::lower_bound(b+1,b+cnt,a[i])-b; int ans=0; for(int i=1;i<=n;++i){ ans+=getsum(a[i]+1); updata(a[i]); } printf("%d\n",ans); } int main(){ Solve(); return 0; }
五、离散化
-
什么是离散化呢?
- 很多时候,我们并不关心数组中每个值的大小,只关心它们的序的关系。
- 在求数组的逆序对的时候,
9 8 7 6 5和5 4 3 2 1具有相同的逆序对 - 我们只关心数组的每个数右边有多少个比当前元素小的数,至于每个数有多大并不重要。
- 在求数组的逆序对的时候,
- 通常我们把 一个具有
n个 unique values 的数组映射到 range[1, n]的整数的操作叫做离散化。 - 如果数组有重复元素,重复元素在离散化后的数组也需要具有相同的值。
- 很多时候,我们并不关心数组中每个值的大小,只关心它们的序的关系。
-
离散化的两种方法:
-
方法一:lower_bound
-
对原始数据进行备份,并对备份数组进行排序。
-
用 \(stl\) 的 \(unique\) 函数对排序后的数组进行去重。
-
二分查找原始数组里每个元素在去重后的备份数组中的位置,并把位置作为数组的新的值。
-
\(Code\)
#include <bits/stdc++.h> const int maxn=1e5+5; int a[maxn],b[maxn];//a为原数组,b为备份数组 int n,cnt; void Solve(){ scanf("%d",&n); srand(time(0)); for(int i=1;i<=n;++i){ a[i]=rand()%(2*n); b[i]=a[i]; } std::sort(b+1,b+n+1);//备份数组排序 cnt=std::unique(b+1,b+n+1)-b-1;//备份数组排序,cnt指向不重的最后一个元素 for(int i=1;i<=n;++i) //二分查找a[i]在数组中的位置,并用相对大小代替原始值。 a[i]=std::lower_bound(b+1,b+cnt+1,a[i])-b; } int main(){ Solve(); return 0; } -
unique 解析:
-
unique 函数的函数原型如下:
iterator unique(iterator it_1,iterator it_2); -
这两个参数表示对容器中 \([it\_1,it\_2)\) 范围的元素进行去重,注意区间是前闭后开 。
-
返回值是一个迭代器,它指向的是去重后容器中不重复序列的最后一个元素的下一个元素。
-
unique 函数的去重过程实际上就是不停的把后面不重复的元素移到前面来,也可以说是用不重复的元素占领重复元素的位置。
-
unique 函数实现过程等价于下面函数:
iterator My_Unique (iterator first, iterator last){ if (first==last) return last; iterator result = first;//result指向最后一个不重复的最后一个元素 while (++first != last){//遍历整个序列 if (!(*result == *first)) //first和result指向的值不相等 *(++result)=*first;//把first指向的值移动到result的下一个位置 }//如果first和result指向值相等,first往后遍历。 return ++result;//把不重复的最后一个元素的下一个位置的迭代器返回。 } -
unique 函数去重一般需要对序列进行排序,否则有可能不能真正的去重。
-
-
-
方法二:排序之后,枚举着放回原数组
-
结构体存下原数和位置。
-
对结构体数组按照元素的值进行排序
-
枚举排序后的数组,\(rank[id]=i\) 离散化数组。
-
\(Code\)
#include <bits/stdc++.h> const int maxn=1e5; struct Node{ int id,data; bool operator <(const Node &a)const{ return data<a.data; } }a[maxn]; int n,rank[maxn]; void Solve(){ scanf("%d",&n); srand(time(0)); for(int i=1;i<=n;++i){ a[i].id=i; a[i].data=rand()%n; } std::sort(a+1,a+n+1); for(int i=1;i<=n;++i) rank[a[i].id]=i; for(int i=1;i<=n;++i) printf("%d ",rank[i]); } int main(){ Solve(); return 0; } -
这种离散化方式没有对相同元素去重,如果需要去重也比较麻烦,一般情况下用第一种方法进行离散化,简单好写还不容易出错。
-
-
六、区间修改单点查询
-
差分思想
- 对一个 \(n\) 个元素的序列 \(\{a_1,a_2,...,a_n \}\) ,令 \(b_i=a_i-a_{i-1}\) ,产生新的序列 \(\{b_1,b_2,...,b_n\}\) ,我们称 序列 \(b\) 为序列 \(a\) 的差分数组。
- 序列 \(a=\{1,8,10,7,10\}\),则其差分序列 \(b=\{1,7,2,-3,3\}\) 。
- 为了方便计算,序列编号一般为\(1\sim n\) ,且默认 \(a_0=0\) 。
- 根据差分的定义,\(b_1=a_1-a_0,b_2=a_2-a_1,...,b_n=a_n-a_{n-1}\) ,由此我们很容易得出:\(a_i=\sum_{j=1}^{i} b_j\) 。
- 对一个 \(n\) 个元素的序列 \(\{a_1,a_2,...,a_n \}\) ,令 \(b_i=a_i-a_{i-1}\) ,产生新的序列 \(\{b_1,b_2,...,b_n\}\) ,我们称 序列 \(b\) 为序列 \(a\) 的差分数组。
-
区间修改单点查询
- 如果我们用树状数组维护原序列的差分序列,我们很容易通过向上更新,向下求和的方式求出原序列的每一个元素。
- 如果我们对原序列的 \([l,r]\) 区间的每一个元素增加 \(x\) ,此时我们只需对树状数组 \(c[l]\) 向上更新 \(x\) ,这样向下查询每一个元素的新的值的时候区间 \([l,n]\) 之间的元素值都增加了 \(x\) ,为了消除对区间 \([r+1,n]\) 之间的元素的影响,我们只需对树状数组 \(c[r+1]\) 处向上更新一个 \(-x\) 即可。
-
代码实现:
#include <bits/stdc++.h> const int maxn=1e6+5; typedef long long ll; ll a[maxn],b[maxn],c[maxn]; int n; int lowbit(int x){return x & -x;} void updata(int i,ll x){ for(;i<=n;i+=lowbit(i)) c[i]+=x; } ll getsum(int i){ ll tot=0; for(;i;i-=lowbit(i)) tot+=c[i]; return tot; } void Solve(){ int Q; scanf("%d%d",&n,&Q); for(int i=1;i<=n;++i){ scanf("%lld",&a[i]); b[i]=a[i]-a[i-1];//差分数组 updata(i,b[i]); } int l,r; ll x; while(Q--){ int flag;scanf("%d",&flag); if(flag==1){ scanf("%d%d%lld",&l,&r,&x); updata(l,x); updata(r+1,-x); } else{ int X; scanf("%d",&X);//查询a[X]。 printf("%lld\n",getsum(X)); } } } int main(){ Solve(); return 0; }
七、区间修改区间查询
-
树状数组的区间查询也是在差分的基础上进行的,有上面的差分可知:
-
\(a_i=\sum_{j=1}^i b_j\)
-
前缀和:\(sum_i=\sum_{j=1}^i a_i=\sum_{j=1}^i\sum_{k=1}^j b_k\) 。
-
\[\begin{aligned} sum_i&=a_1+a_2+...+a_i\\ &=b_1+(b_1+b_2)+...+(b_1+b_2+..+b_i)\\ &=i*b_1+(i-1)*b_2+...+2*b_{i-1}+b_i\\ &=i*(b_1+b_2+...+b_i)-(0*b_1+1*b_2+...+(i-1)*b_i)\\ &=i*\sum_{j=1}^i b_j-(0*b_1+1*b_2+...+(i-1)*b_i) \end{aligned} \]
-
所以我们只需用一个树状数组维护 \(b_i\) ,一个树状数组维护 \((i-1)*b_i\) 即可。
-
\(Code\)
#include <bits/stdc++.h> const int maxn=1e6+5; typedef long long ll; ll a[maxn],c1[maxn],c2[maxn]; int n; int lowbit(int x){return x & -x;} void updata(int x,ll w){ for(int i=x;i<=n;i+=lowbit(i)) { c1[i]+=w;//维护差分数组 c2[i]+=(x-1)*w;//维护(i-1)*bi } } ll getsum(int x){ ll tot=0; for(int i=x;i;i-=lowbit(i)) tot+=x*c1[i]-c2[i]; return tot; } void Solve(){ int Q; scanf("%d%d",&n,&Q); for(int i=1;i<=n;++i){ scanf("%lld",&a[i]); updata(i,a[i]-a[i-1]); } int l,r; ll x; while(Q--){ int flag;scanf("%d",&flag); if(flag==1){ scanf("%d%d%lld",&l,&r,&x); updata(l,x); updata(r+1,-x); } else{ scanf("%d%d",&l,&r); printf("%lld\n",getsum(r)-getsum(l-1)); } } } int main(){ Solve(); return 0; }
-




