有依赖的背包问题

有依赖的背包问题

问题模型

• 有 \(N\) 个物品和一个容量是 \(V\) 的背包。物品之间具有依赖关系，且依赖关系组成一棵树的形状。如果选择一个物品，则必须选择它的父节点。
  如下图所示：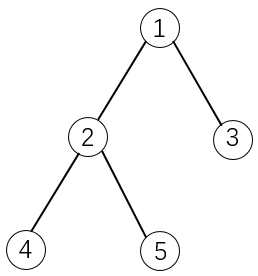
• 
• 如果选择物品 \(5\)，则必须选择物品 \(1\) 和 \(2\) 。这是因为 \(2\) 是 \(5\) 的父节点，\(1\) 是 \(2\) 的父节点。
  每件物品的编号是 \(i\)，体积是 \(v_i\)，价值是 \(w_i\)，依赖的父节点编号是 \(p_i\)。物品的下标范围是 \(1…N\)。
• 求解将哪些物品装入背包，可使物品总体积不超过背包容量，且总价值最大。输出最大价值。

输入格式

第一行有两个整数 \(N,V\)，用空格隔开，分别表示物品个数和背包容量。

接下来有 \(N\) 行数据，每行数据表示一个物品。

第 \(i\) 行有三个整数 \(v_i,w_i,p_i\)，用空格隔开，分别表示第 \(i\) 物品的体积、价值和依赖的物品编号。如果 \(p_i=−1\)，表示根节点。 数据保证所有物品构成一棵树。

输出格式

输出一个整数，表示最大价值。

输入样例

5 7
2 3 -1
2 2 1
3 5 1
4 7 2
3 6 2

样例输出

11

数据范围

\(1\le N,V\le 100,1\le v_i,w_i\le 100\)

分析

有依赖的背包目前见的题目比较少，顾名思义，有依赖的背包里的物品的选择是有依赖的，即选择一个物品，就必须先选某个物品。这个必须先选的物品我们称之为依赖物品。

一般地，某个物品的依赖物品只有一个（如果有多个的话可以考虑把出题人挂在树上）（但某个物品可以同时被多个物品依赖）

首先我们得表示出来物品的依赖关系，考虑到物品 \(i\) 的依赖物品只有 \(1\) 个，所以可以用父子关系来表示，自然而然的想到用树。

• 对于物品 \(i\) ,我们要 \(dp\) 出以 \(i\) 为根的子树中，体积为 \(j\) 时的最大权值和。
• 考虑 \(i\) 的每个儿子，（由于是从下往上 \(dp\) ,所以 \(i\) 的儿子的 \(dp\) 值已经算好了）我们需要考虑从以 \(i\) 的第 \(j\) 个儿子为根的子树中选几个节点;
• 同时我们已经知道了第 \(j\) 个儿子的所有 \(dp\) 值，所以不妨把以第 \(j\) 个儿子为根的子树看做一组物品，且我们已经知道分配给这组物品 \(x\) 的体积时，最大值是多少。
• 所以就相当于对每个节点做分组背包。同时注意一点，在考虑以 \(i\) 为根的子树的时候，点 \(i\) 是必选的，要注意这一点。

Code

#include <bits/stdc++.h>
const int maxn=1e2+5,maxv=1e2+5;
struct Edge{
	int to,next;
}e[maxn];
int dp[maxn][maxv];//dp[i][j]:表示以i为根的子树包括i在j的背包的最大价值
int N,V,w[maxn],c[maxn],p[maxn];
int head[maxn],len;
void Insert(int u,int v){
	e[++len].to=v;e[len].next=head[u];head[u]=len;
}
void dfs(int u,int fa){
	for(int i=head[u];i;i=e[i].next){//遍历u为根的子树
		int v=e[i].to;
		if(v==fa)continue;//建立的是单向边，这句其实是废话
		dfs(v,u);//dp[v][j]求以v为根的子树包括根v，j的背包的最大价值
		for(int j=V-w[u];j>=w[v];--j)//以u为根的子树，此时未包含根u，所以最多能用V-w[u]的背包
			for(int k=w[v];k<=j;++k)//以v为根的子树使用了k的背包容量，其他已处理的u的其他子树占了j-k的背包
				dp[u][j]=std::max(dp[u][j],dp[u][j-k]+dp[v][k]);//此时dp[v][k]包含了根v的最优，dp[u][j]和dp[u][j-k]均未包含根u
	}
	for(int i=V;i>=0;--i)//更新下dp[u][i]数组，把根u放到背包里去
		if(i<w[u])dp[u][i]=0;//此处坑点，一定要给清0,因为不足w[u]的背包根本就放不下u,所以为0
		else dp[u][i]=dp[u][i-w[u]]+c[u];//能放下u的背包把u放进去
}
void Solve(){
	scanf("%d%d",&N,&V);
	for(int i=1;i<=N;++i){
		scanf("%d%d%d",&w[i],&c[i],&p[i]);
		if(p[i]==-1)Insert(0,i);//把0作为树根
		else Insert(p[i],i);
	}
	dfs(0,-1);
	printf("%d\n",dp[0][V]);
}
int main(){
	Solve();
	return 0;
}

时间效率：每个点均要访问一次，对每个点来说需要 \(v^2\)，总的时间效率为：\(O(n*v^2)\)。

金明的预算方案

• 此题的出现才提出了依赖背包的模型，可以说是依赖背包的开山之作，但此题的数据范围 \(v\le 3.2 e 4\) 显然上面的方法无法解决，实际上用上面的模板只能拿到 \(40\)分.

• 我们来分析下此题和模板的不同，模板就是一棵树，树的深度没有限制，节点的儿子数也没有限制，而此题是一个森林，深度最大为2,儿子节点u最多有2个，所以对每一个依赖来说，最多有五种可能：

  1. 一个都不选
  2. 只选主件
  3. 选主件和附件1
  4. 选主件和附件2
  5. 选主件和附件1、附件2

• 这样对于没一组依赖问题就可以最多转化为5个单独的物品，这五个物品具有排他性，这就成了典型的分组背包问题。

• Code1(bug)

  #include <bits/stdc++.h>
  const int maxn=60+5,maxv=3e4+5;
  int n,m;
  int w[maxn],c[maxn];//w[i],c[i]主件i的体积和价值
  int fw[maxn][3],fc[maxn][2];//fw[i][0],fw[i][1],fw[i][2]主件i的附件个数，附件1的体积，附件2的体积，fc类似
  int dp[maxv];//dp[i]在体积i的情况下的最大值
  bool vis[maxn];//vis[i]记录i是否为主件
  void Solve(){
  	scanf("%d%d",&n,&m);
  	for(int i=1;i<=m;++i){
  		int v,p,q;scanf("%d%d%d",&v,&p,&q);
  		if(!q){//i是主件
  			w[i]=v;c[i]=v*p;vis[i]=1;
  		}
  		else{//如果i是附件
  			fw[q][++fw[q][0]]=v;
  			fc[q][++fc[q][0]]=v*p;
  		}
  	}
  	for(int i=1;i<=m;++i){
  		if(!vis[i])continue;//如果是附件就pass
  		for(int j=n;j>=w[i];--j){
  			dp[j]=std::max(dp[j],dp[j-w[i]]+c[i]);//考虑主件选与不选
  			if(fw[i][0]>0 && j>=w[i]+fw[i][1])//
  				dp[j]=std::max(dp[j],dp[j-w[i]-fw[i][1]]+c[i]+fc[i][1]);
  			if(fw[i][0]>1 && j>=w[i]+fw[i][2])
  				dp[j]=std::max(dp[j],dp[j-w[i]-fw[i][2]]+c[i]+fc[i][2]);
  			if(fw[i][0]>1 && j>=w[i]+fw[i][2]+fw[i][1])
  				dp[j]=std::max(dp[j],dp[j-w[i]-fw[i][1]-fw[i][2]]+c[i]+fc[i][1]+fc[i][2]);
  		}
  	}
  	printf("%d\n",dp[n]);
  }
  int main(){
  	Solve();
  	return 0;
  }
  

• 上面这份代码是网上题解最多的代码，这份代码结果不能算错，但是在转移上是存在问题的，因为数据范围 \(0\le v_i\le 10^4\) 就是说附件的体积可以为 0 ，如果某个主、附件的体积为0，那么就造成 \(dp[j]==dp[j-w[i]]==dp[j-w[i]-fw[i][1]]\) ，那么我们在转移的时候就可能造成主件就会被重复计算，比如在计算完主件 \(dp[j]\) 已经是包含了主件的最优，再考虑附件1时，因为主件和附件的体积为0，附件1转移时也是从已经选了主件的 \(dp[j]\) 转移过来，这样主件就被选了两次。

• 不过此题不存在这样的问题，因为转移的价值是：\(v[i]*p[i]\) 当\(v[i]==0\) 时，实际上没有产生更多的价值，所以此题这样写也是没问题的。但遇到这样的问题以后最好写成滚动数组，让当前状态严格的从上一轮决策里转移过来。

• Code2

  #include <bits/stdc++.h>
  const int maxn=60+5,maxv=3e4+5;
  int n,m;
  int w[maxn],c[maxn];//w[i],c[i]主件i的体积和价值
  int fw[maxn][3],fc[maxn][3];//fw[i][0],fw[i][1],fw[i][2]主件i的附件个数，附件1的体积，附件2的体积，fc类似
  int dp[2][maxv];//dp[i]在体积i的情况下的最大值
  bool vis[maxn];//vis[i]记录i是否为主件
  void Solve(){
  	scanf("%d%d",&n,&m);
  	for(int i=1;i<=m;++i){
  		int v,p,q;scanf("%d%d%d",&v,&p,&q);
  		if(!q){//i是主件
  			w[i]=v;c[i]=v*p;vis[i]=1;
  		}
  		else{//如果i是附件
  			fw[q][++fw[q][0]]=v;
  			fc[q][++fc[q][0]]=v*p;
  		}
  	}
  	int x=0;
  	for(int i=1;i<=m;++i){
  		if(!vis[i])continue;//如果是附件就pass
  		x=!x;//滚动数组
  		for(int j=n;j>=0;--j){//注意滚动数组j一定要遍历到0
  			if(j<w[i])dp[x][j]=dp[!x][j];//注意：不能放i这个主件可能放了其他主件
  			if(j>=w[i])
  				dp[x][j]=std::max(dp[!x][j],dp[!x][j-w[i]]+c[i]);//考虑主件选与不选
  			if(fw[i][0]>0 && j>=w[i]+fw[i][1])
  				dp[x][j]=std::max(dp[x][j],dp[!x][j-w[i]-fw[i][1]]+c[i]+fc[i][1]);
  			if(fw[i][0]>1 && j>=w[i]+fw[i][2])
  				dp[x][j]=std::max(dp[x][j],dp[!x][j-w[i]-fw[i][2]]+c[i]+fc[i][2]);
  			if(fw[i][0]>1 && j>=w[i]+fw[i][2]+fw[i][1])
  				dp[x][j]=std::max(dp[x][j],dp[!x][j-w[i]-fw[i][1]-fw[i][2]]+c[i]+fc[i][1]+fc[i][2]);
  		}
  	}
  	printf("%d\n",dp[x][n]);
  }
  int main(){
  	Solve();
  	return 0;
  }