最短路径

最短路径(思维好题 \(\star\star\star \))

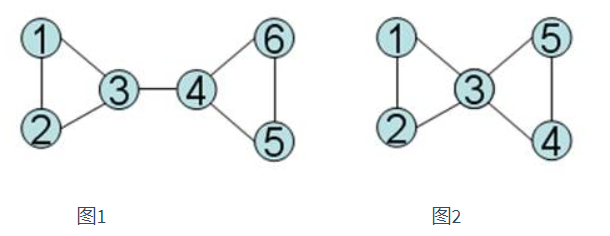
• 一个特殊的无向连通图，它有 \(n\) 个结点 \(m\) 条边，图中存在若干个环，但是，每个结点最多只会属于一个简单环。例如，图 \(1\) 所示的图符合我们的要求，但图 \(2\) 则不符合我们的描述，因为 \(3\) 号结点属于两个简单环。

  

• 给出这样的一个无向图，你需要计算两个点的最短距离。

Input

• 第一行 \(2\) 个整数 \(n,m\)，表示结点数和边数；
• 接下来 \(m\) 行，每行 \(3\) 个整数 \(x,y,z\)，表示结点 \(x\) 和 \(y\) 之间存在一条边权为 \(z\) 的边。
• 再接下来 \(1\) 行包含一个整数 \(q\)，表示询问数量；
• 之后 \(q\) 行，每行 \(2\) 个整数 \(x,y\)，表示询问结点 \(x\) 和 \(y\) 的最短距离。

Output

• 对于每个询问输出一行一个整数，表示最短距离 。

Sample Input

4 4
1 2 1
2 3 2
1 3 2
3 4 1
2
2 4
1 3

Sample Output

3
2

Hint

• 对于\(30\%\) 的数据，\(N≤100\)；
• 另有 \(30\%\) 的数据，保证 \(N=M\)；
• 对于 \(100\%\) 的数据，\(1≤N≤100,000,Q≤200,000,1≤x,y≤N,1≤z≤1000\) 。
• 来源：\(20180714,bzoj2125,luogu5236\)

分析

• 整个图为一个仙人掌图。先用 \(DFS\) 遍历整个图，同时找出所有的环。对于每个环，将环上第一个被遍历到的点设为“父亲”，环上其它点都与该点连长度为 \(0\) ，再删去所有环上的边。这样就变成了一棵树。
• 在处理环之前，先求出 \(1\) 到其他点的最短距离 \(dis_i\) 在第一遍 \(dfs\) 过程中，维护一个数组 \(rd[i]\) 表示 \(i\) 到根的距离，便于求环上两点间的距离。
• 在 \(dfs\) 过程中遇到返祖边，然后对环上的边和点进行标记，同时求出环的长度。
• 最后再新生成的树上求 \(lca\) ，对于询问 \(u,v\) ，如果 \(lca(u,v)\) 不在环上，显然他们的距离为：\(dis[u]+dis[v]-2*dis[lca(u,v)]\) 。
• 如果 \(lca(u,v)\) 在环上，假设 \(x\) 是 \(u\) 在环上的祖先节点，\(y\) 是 \(v\) 在环上的祖先节点，在环上 \(x\rightarrow y\) 的距离为：\(r=abs(rd[x]-rd[y])\) 或者为：环的周长\(-r\) 。

Code

#include <bits/stdc++.h>
const int maxn=100005+100,maxm=300005;//因为有新增边，最大新增边为n，即一个大环
struct Node{
    int to,w,next;
}e[maxm];
int len=1,head[maxn],vis[maxn],dis[maxn],dep[maxn],f[maxn][14];
int n,m,Time,dfn[maxn];
int cnt,Circle[maxm],st[maxn],rd[maxn],belong[maxn],Girth[maxn];
void Insert(int x,int y,int z){//边的编号从2开始    
    e[++len].to=y;e[len].w=z;e[len].next=head[x];head[x]=len;
}
void spfa(int x) {
    memset(dis,0x3f,sizeof dis);
    std::queue<int> q; q.push(x);dis[x]=0;
    while(!q.empty()) {
        int u=q.front(); q.pop();vis[u]=0;
        for(int i=head[u];i;i=e[i].next){
            int v=e[i].to;
            if(dis[v]>dis[u]+e[i].w){
                dis[v]=dis[u]+e[i].w;
                if(!vis[v])
                    vis[v]=1,q.push(v);
            }
        }
    }
}
void Circ(int x,int y) {//y是环上最早访问的节点
    if(x==y) return;
    belong[x]=cnt;//记录节点x属于哪个环
    Insert(y,x,0);//只需要建y到x的边即可，因为lca时y时x的父亲节点
    Circle[st[x]]=Circle[st[x]^1]=1;//环上的边左上标记
    Girth[cnt]+=e[st[x]].w;//记录环的长度
    Circ(e[st[x]^1].to,y); 
}
void dfs(int x) {
    dfn[x]=++Time;
    for(int i=head[x];i;i=e[i].next){
        int v=e[i].to;
        if(i!=(st[x]^1)&&i<=m*2+1){//编号大于2*m+1的边是新建的环上的边
            if(!dfn[v]){
                rd[v]=rd[x]+e[i].w;//按搜索顺序记录v到根节点1的距离
                st[v]=i;//记录以v结尾的树枝边的编号
                dfs(v);
            } 
            else if(dfn[v]<dfn[x]){//出现简单环
                Girth[++cnt]=e[i].w;//cnt记录环的编号
                Circ(x,v);//处理环,v是环上最早访问的点
            } 
        }
    }
}
void dfs2(int u) {
    for(int i=1;(1<<i)<=dep[u];++i)
        f[u][i]=f[f[u][i-1]][i-1];
    for(int i=head[u];i;i=e[i].next){
        int v=e[i].to;
        if(!Circle[i] && !dep[v]){//边i不在环上v未访问
            f[v][0]=u;//倍增初始化
            dep[v]=dep[u]+1;
            dfs2(v);
        }
    }
}
int Query(int u,int v) {
    if(dep[u]<dep[v])std::swap(u,v);
    int a=u,b=v,len=dep[u]-dep[v],k=0;
    while(len){
        if(len & 1) u=f[u][k];
        ++k;len>>=1;
    }
    if(u==v)return dis[a]-dis[b];
    for(int i=13;i>=0;i--)
        if(f[u][i]!=f[v][i]){
            u=f[u][i];v=f[v][i];
        }
    if(belong[u] && belong[u]==belong[v]) {
        int r=abs(rd[u]-rd[v]);//u和v按搜索顺序在环的距离
        return dis[a]-dis[u]+dis[b]-dis[v]+std::min(r,Girth[belong[u]]-r);
    }
    return dis[a]+dis[b]-2*dis[f[u][0]];
}

int main() {
    scanf("%d%d",&n,&m);
    for(int i=1;i<=m;i++){
        int x,y,z;scanf("%d%d%d",&x,&y,&z);
        Insert(x,y,z);Insert(y,x,z);
    }
    spfa(1),dfs(1),dep[1]=1,dfs2(1);
    int q;scanf("%d",&q);
    while(q--){
        int x,y;scanf("%d%d",&x,&y);
        printf("%d\n",Query(x,y));
    }
    return 0;
}