搜城探宝
搜城探宝 (树型dp \(\star\))
-
\(zhclk\) 已经坚信自己就是传说中的有缘人，于是，带着梦想，带着希冀，带着勇气，来到了神迹，寻找……
-
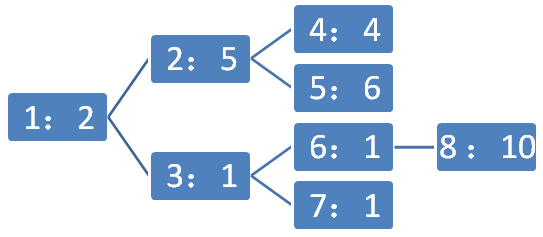
如下图，神迹的城堡是一个树形的结构，共有 \(n\) 间屋子。每间屋子都有一把锁，并且每间屋子最多可以到另外的两个屋子里（它是一棵二叉树）。在城堡的每个房间都存在着不同的宝藏。现在 \(zhclk\) 站在城堡的大门口（\(1\) 号屋子门口）拥有 \(k\) 把万能钥匙，可以打开任意一把锁，但每把钥匙只能用一次，钥匙是拔不出来的。
-
问题哪有那么简单……，\(Zhclk\) 还有一个传送门，可以在任何时候带他去任何一间屋子，但传送门也只能 使用一次。
-
地图上画出了宝藏的分布，只有获得最大价值的宝藏 \(zhclk\) 的目的才能实现。
Input
- 第一行：两个数 \(n\) 和 \(k\)。为城堡的屋子总数和你拥有的万能钥匙数。
- 第二行到第 \(n\) 行：每行两个数 \(x_1\) 和 \(x_2\)，为树上的 \(n-1\) 条边。（树保证以 \(1\) 为根节点）。
- 第 \(n+1\) 行：\(n\) 个数，第 \(i\) 个数为房间 \(i\) 的宝藏价值 \(v_i\)。
Output
- 一个数，为最大宝藏价值 \(maxv\)。
Sample Input
8 4
1 2
1 3
2 4
2 5
3 6
3 7
6 8
2 5 1 4 6 1 1 10
Sample Output
27
Hint
- 用钥匙依次开$1, 2, 4, 5 $ 号房间，再用传送门去 \(8\) 号房间，\(27=2+5+6+4+10\) 。
- 数据范围： \(n<=20\) 。
- 来源：
分析
- 题目说白了就是树规，但是题目中的传送门增加了问题的不确定性，所以直接上裸的树规肯定是要爆掉的。记使用传送门从 \(x\) 到 \(y\)，不难证明有以下结论:
- \(y\) 仅限于没有访问过的节点，当然更不是 \(x\) 的祖先。
- 可以将 \(y\) 从整棵树中独立出来求 \(dp\) 值，并且这样做是正确的。
- 可以规定传送到 \(y\) 之后不能再往祖先方向走（断掉）。
- 在 \(x\) 节点使用传送门等效于回到 \(x\) 的任意一个祖先之后再使用传送门。因此，可以选择从整棵树的虚根\(n+1\) 使用传送门，再令 \(1\) 为 \(n+1\) 的左儿子，那么整棵树(除去 \(y\) )的 \(dp\) 值都好计算了。
- 既然要把 \(y\) 独立出去计算其 \(dp\) 值，那么可以令 \(y\) 为 \(n+1\) 的右儿子。
- 有了以上结论，问题的解决就变得十分容易了。
- 首先令 \(n+1\) 的左儿子为 \(1\)，然后从 \(2\) 到 \(n\) 枚举 \(y\) (也就是被挂出去的节点)，把 \(y\) 设置为 \(n+1\) 的右儿子，对树 \(n+1\) 进行一次树形 \(dp\)。
- 细节问题：
- 开虚根的门需要一个钥匙，去 \(y\) 需要一个钥匙(但是实际上传送门自带钥匙)，因此钥匙数要 \(+2\)。
- 复杂度：
- 枚举 \(y\) 需要 \(O(n)\) 次，每个点计算一次总共 \(O(n)\) 次，每个点的状态转移需要 \(O(m)\) 的时间，所以总时间复杂度为\(O(n^2m)\)。
- 令 \(f(i,j)\) 为树 \(i\) 的最大 \(dp\) 值，显然空间复杂度为 \(O(nm)\)。
- 考虑到 \(m>n\) 的情况等同于 \(m=n\) 的情况(这是显然的，因为门不够再多钥匙也没什么卵用)，故可以认为时间复杂度为 \(O(n^3)\)，空间复杂度为 \(O(n^2)\)。
Code
#include <bits/stdc++.h>
const int maxn=20+5;
int n,k,a[maxn],ans=0;
int fa[maxn],ls[maxn],rs[maxn];
int dfs(int x,int sum){
if(x==0)return 0;//搜完叶子
if(sum==1)return a[x];//只剩下一把钥匙
int now=0;
for(int i=0;i<sum;++i)//树归
now=std::max(now,dfs(ls[x],i)+dfs(rs[x],sum-1-i)+a[x]);
return now;
}
void Init(){
scanf("%d%d",&n,&k);
for(int i=1;i<n;++i){
int x,y;scanf("%d%d",&x,&y);
if(!ls[x])ls[x]=y;
else rs[x]=y;
fa[y]=x;
}
for(int i=1;i<=n;++i)
scanf("%d",&a[i]);
}
void Solve(){
ls[n+1]=1;//虚根，原根作为左儿子
for(int i=2;i<=n;++i){//枚举其他点，作为右儿子
rs[n+1]=i;//把i作为右儿子，增加钥匙一把
if(ls[fa[i]]==i){//i是左儿子
ls[fa[i]]=0;//先断掉
ans=std::max(dfs(n+1,k+2),ans);//增加了2把钥匙所以是k+2
ls[fa[i]]=i;//重新续上
}
else{//i是右儿子
rs[fa[i]]=0;//断掉
ans=std::max(dfs(n+1,k+2),ans);
rs[fa[i]]=i;//续上
}
}
printf("%d\n",ans);
}
int main(){
Init();
Solve();
return 0;
}
hzoi
