免费馅饼
免费馅饼 (dp \(\star\))
-
\(SERKOI\) 最新推出了一种叫做“免费馅饼”的游戏:
- 游戏在一个舞台上进行。舞台的宽度为 \(W\) 格，天幕的高度为 \(H\) 格，游戏者占一格。
- 开始时游戏者站在舞台的正中央，手里拿着一个托盘。下图为天幕的高度为 \(4\) 格时某一个时刻游戏者接馅饼的情景。
-
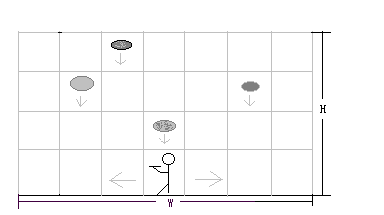
游戏开始后，从舞台天幕顶端的格子中不断出现馅饼并垂直下落。游戏者左右移动去接馅饼。游戏者每秒可以向左或向右移动一格或两格，也可以站在原地不动。
-
馅饼有很多种，游戏者事先根据自己的口味，对各种馅饼依次打了分。同时，在 \(8-308\) 电脑的遥控下，各种馅饼下落的速度也是不一样的，下落速度以格/秒为单位。
-
当馅饼在某一秒末恰好到达游戏者所在的格子中，游戏者就收集到了这块馅饼。
-
写一个程序，帮助我们的游戏者收集馅饼，使得所收集馅饼的分数之和最大。
Input
- 输入文件的第一行是用空格隔开的两个正整数，分别给出了舞台的宽度 \(W\)（\(1\) 到 \(99\) 之间的奇数）和高度 \(H\)（ \(1\) 到 \(100\) 之间的整数）。
- 接下来依馅饼的初始下落时间顺序给出了所有馅饼的信息。每一行给出了一块馅饼的信息。由四个正整数组成，分别表示了馅饼的初始下落时刻（\(0\) 到 \(1000\) 秒），水平位置、下落速度（\(1\) 到 \(100\)）以及分值。游戏开始时刻为 \(0\)。从 \(1\) 开始自左向右依次对水平方向的每格编号。
- 输入文件中同一行相邻两项之间用一个或多个空格隔开。
Output
- 输出文件的第一行给出了一个正整数，表示你的程序所收集的最大分数之和。
- 其后的每一行依时间顺序给出了游戏者每秒的决策。
- 输出 \(0\) 表示原地不动、\(1\) 或 \(2\) 表示向右移动一步或两步、\(-1\) 或 \(-2\) 表示向左移动一步或两步。
- 输出应持续到游戏者收集完他要收集的最后一块馅饼为止。
- 注意：
- 输出数字的字典序最小的方案。
- 馅饼可以掉到高度小于 \(1\) 的格子（例：速度为 \(5\) 的馅饼，从高度 \(4\) 处掉到高度 \(-1\) 处，而不是高度 \(1\)）
Sample Input
3 3
0 1 2 5
0 2 1 3
1 2 1 3
1 3 1 4
Sample Output
12
-1
1
1
Hint
- 馅饼个数 \(\in [0,2500]\)
分析
- 一道移动DP题。这题初看无从下手，馅饼和人都在移动，但仔细分析可得：定馅饼不动，由人移动去接馅饼。
- 但要想好两点：
- 只有高度可以被下落速度整除时，该馅饼才有可能被接到，所以很多馅饼是废的。
- 时间可以当做纵坐标轴来处理，即。
- 设 \(f[i][j]\) ，\(i\) 表示时刻，\(j\) 表示 \(x\) 坐标。用 \(k\) 枚举移动的距离（\(k\) 可为\(-2，-1,0,1,2\)）。
- 动态转移方程：\(f[i][j]=max(f[i-1][j+k]+a[i][j])\);
Code
#include <bits/stdc++.h>
const int maxn=2500+5;
int w,h,n,Time;
int f[maxn][101];
int c[maxn],x[maxn],t[maxn],v[maxn];
void Read(){
scanf("%d%d",&w,&h);
h--;//馅饼就在最高一格出现
int T,X,V,C;
while(scanf("%d%d%d%d",&T,&X,&V,&C)==4){
if(h%V==0){//到达不了舞台的不用管
t[++n]=T+h/V;
x[n]=X;v[n]=V;c[n]=C;
Time=std::max(Time,t[n]);//记录最大的到达舞台的馅饼时间
}
}
memset(f,0,sizeof(f));
}
int mx(int i,int j){
int ans=0;
for(int k=-2;k<=2;++k){
if(j+k<0 || j+k>w)continue;
ans=std::max(ans,f[i+1][j+k]);
}
return ans;
}
void Solve(){
if(!n){//n==0说明没有一个能掉到舞台的
printf("0\n");return;
}
for(int i=1;i<=n;i++)//初始化
f[t[i]][x[i]]+=c[i];//有可能不同时刻的馅饼可能同时掉在舞台同一个位置
for(int i=Time-1;i>=0;i--)//从上往下好处理
for(int j=w;j>0;j--) //因为转移是有范围的
f[i][j]+=mx(i,j);
printf("%d\n",f[0][w/2+1]);
}
int main(){
Read();
Solve();
return 0;
}
hzoi
