最大子段和之基础模型
最大子段和
一、 最大子段和基础模型
题目模型
-
给定
n个整数(可能为负数)组成的序列\(a_1,a_2,...,a_n\) ,求该序列如:\(a_{i}+a_{i+1}+...+a_j\ i\le j\) 的子段和的最大值。当所给的整数均为负数时定义子段和为0。 -
即:\(ans=max(0,\sum_{i=l}^r a_i),\ (1\le l\le r\le n\le 10^7)\) 。
问题分析
方法一:前缀和
-
很容易想到 \(O(n^2)\) 枚举所有区间\([l,r]\) ,\(O(n)\) 的效率求出区间和。总时间效率为\(O(n^3)\) 。
-
维护序列的前缀和,利用差分思想,很容易把区间和优化到\(O(1)\)。总时间效率为\(O(n^2)\)。
-
\(n\) 高达千万,要想在 \(1s\) 内解决问题,需要把时间效率降到\(O(n)\) 级别。
-
假设区间\([l,r]\),区间和\(sum=sum[r]-sum[l-1]\)我们固定左边界\(r\),从\(1\sim r\) 中找到前缀和最小的\(l\)。
-
所以我们只需要\(O(n)\) 去遍历序列,遍历的同时维护一下已遍历区间最小前缀和即可。
-
Code#include<bits/stdc++.h> using namespace std; typedef long long LL; const int maxn=1e7+5,maxm=1e5+5; const LL Inf=0x3f3f3f3f3f3f3f3f; LL a[maxn],sum[maxn]; int n; void Solve(){ srand(time(0)); scanf("%d",&n); LL Min=0,ans=0;//Min初始化为0,因为如果序列元素均为正数的时候,此时我们去最小前缀为0 for(int i=1;i<=n;++i){ a[i]=rand()%10000-5000; sum[i]=sum[i-1]+a[i]; Min=std::min(Min,sum[i]); ans=std::max(ans,sum[i]-Min); } printf("%lld\n",ans); } int main(){ Solve(); return 0; }
-
-
我们稍微修改一下代码就可以解决最大子段和不能为空的问题
-
Code#include<bits/stdc++.h> using namespace std; typedef long long LL; const int maxn=1e7+5,maxm=1e5+5; const LL Inf=0x3f3f3f3f3f3f3f3f; LL a[maxn],sum[maxn]; int n; void Solve(){ srand(time(0)); scanf("%d",&n); LL Min=0,ans=-Inf;//Min初始化为0,因为不可以为空,所以最大子段和可能为负,所以ans=-Inf。 for(int i=1;i<=n;++i){ a[i]=rand()%10000-5000; sum[i]=sum[i-1]+a[i]; ans=std::max(ans,sum[i]-Min);//此时的Min肯定不会包含a[i],所以答案至少会取一个元素 Min=std::min(Min,sum[i]); } printf("%lld\n",ans); } int main(){ Solve(); return 0; }
方法二:动态规划
-
定义状态
f[i]表示以i结尾的最大子段和(可以为空)。 -
转移方程:\(f[i]=max(f[i-1]+a[i],0)\)
- 显然,如果\(f[i-1]+a[i]<0\) 直接置空,大于零,区间还有成长的空间。
- 最终结果为:\(ans=max(ans,f[i])\ 0< i\le n\)。
-
Code#include<bits/stdc++.h> using namespace std; typedef long long LL; const int maxn=1e7+5,maxm=1e5+5; const LL Inf=0x3f3f3f3f3f3f3f3f; LL f[maxn],a[maxn],ans; int n; void Solve(){ srand(time(0)); scanf("%d",&n); for(int i=1;i<=n;++i){ a[i]=rand()%10000-5000; f[i]=std::max(f[i-1]+a[i],0LL); ans=std::max(ans,f[i]); } printf("%lld\n",ans); } int main(){ Solve(); return 0; }
方法三:分治
-
通过分治的思想求最大子段和,将数组分平均分为两个部分,则最大子段和会存在于三种情况下:
- 最大子段和出现在左端
- 最大子段和出现在右端
- 最大子段和横跨在左右段 通过比较大小得到最大子段和
-
Code#include<bits/stdc++.h> using namespace std; typedef long long LL; const int maxn=1e7+5,maxm=1e5+5; const LL Inf=0x3f3f3f3f3f3f3f3f; LL a[maxn]; int n; LL MaxSum(int l,int r){ LL sum=0,midSum=0,leftSum=0,rightSum=0; if(l==r) sum=a[l]; else{ int mid=(l+r)/2; LL leftSum=MaxSum(l,mid); //情况1,最大字段和全部取左边元素 LL rightSum=MaxSum(mid+1,r);//情况2,最大字段和全部取右边元素 LL tot=0,sumleft=0,sumright=0; //情况3 最大子段和横跨中间 for(int i=mid;i>=l;i--){ //求出从中间a[mid]到左边的最大和 tot+=a[i]; if(tot>sumleft) sumleft=tot; } tot=0; for(int i=mid+1;i<=r;++i){ //求出从中间a[mid+1]到右边的最大和 tot+=a[i]; if(tot>sumright) sumright=tot; } LL midSum=sumleft+sumright; //横跨中间的最大字段和为 sum=std::max(midSum,std::max(leftSum,rightSum));//取三者较大者 } return sum; } void Solve(){ srand(time(0)); scanf("%d",&n); for(int i=1;i<=n;++i){ a[i]=rand()%10000-5000; } printf("%lld\n",MaxSum(1,n)); } int main(){ Solve(); return 0; }
二、单点修改,区间查询的最大子段和
题目模型
-
我们对问题进行扩展,如果对序列有两种操作:
- 修改序列的某个元素的值
- 查询序列\([l,r]\)的区间和。
-
题目模型见P4513 小白逛公园
问题分析
- 单点修改,区间查询显然要用线段树。
- 类似上面分治,区间最大字段和有三种情况:
- 最大子段和在左子树。
- 最大子段和在右子树。
- 左子树的最大后缀和+右子树的最大前缀和。
代码实现
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=5e5+10;
#define lson l,mid,(rt<<1)
#define rson mid+1,r,(rt<<1|1)
struct Tree{
int presum,sufsum,sub,sum;//presum为当前区间最大前缀和,sufsum为当前区间最大后缀和,sub为当前区间最大子段和,sum为当前区间的和
}tree[maxn<<2];
Tree pushup(Tree l,Tree r){//合并左右两区间
Tree rt;
rt.presum=max(l.presum,l.sum+r.presum);//当前区间的最大前缀和:左子树的最大前缀和 or 左子树的和+右子树的最大前缀和
rt.sufsum=max(r.sufsum,r.sum+l.sufsum);//当前区间的最大后缀和:右子树的最大后缀和 or 右子树的和+左子树的最大后缀和
rt.sub=max(max(l.sub,r.sub),l.sufsum+r.presum);//当前区间的最大子段和:左子树的最大子段和 or 右子树的最大子段和 or 左子树的最大后缀和+右子树的最大前缀和
rt.sum=l.sum+r.sum;//当前区间的和:左子树的和+右子树的和
return rt;
}
void build(int l,int r,int rt){
if(l==r){
scanf("%d",&tree[rt].sum);
tree[rt].presum=tree[rt].sufsum=tree[rt].sub=tree[rt].sum;
return ;
}
int mid=(l+r)>>1;
build(lson);
build(rson);
tree[rt]=pushup(tree[rt<<1],tree[rt<<1|1]);
}
void update(int pos,int w,int l,int r,int rt){//把pos个元素修改成值w
if(l==r){
tree[rt].presum=tree[rt].sufsum=tree[rt].sub=tree[rt].sum=w;
return ;
}
int mid=(l+r)>>1;
if(pos<=mid) update(pos,w,lson);
if(pos> mid) update(pos,w,rson);
tree[rt]=pushup(tree[rt<<1],tree[rt<<1|1]);
}
Tree query(int L,int R,int l,int r,int rt){
if(L<=l&&r<=R)
return tree[rt];
int mid=(l+r)>>1;
Tree ret,lret,rret;
int flag1=0,flag2=0;//flag1标记区间[L,R]是否在rt的左子树,flag2右子树
if(L<=mid) {lret=query(L,R,lson);flag1=1;}
if(R> mid) {rret=query(L,R,rson);flag2=1;}
if(flag1&&flag2) ret=pushup(lret,rret);//左右子树均有就合并计算
else if(flag1) ret=lret;//只在左子树
else if(flag2) ret=rret;//只在右子树
return ret;
}
void Solve(){
int n,m;scanf("%d%d",&n,&m);
build(1,n,1);
for(int i=1;i<=m;i++){
int op;
scanf("%d",&op);
if(op==1){
int l,r;
scanf("%d%d",&l,&r);
if(l>r) swap(l,r);
Tree ans=query(l,r,1,n,1);
printf("%d\n",ans.sub);
}
else{
int p,s;
scanf("%d%d",&p,&s);
update(p,s,1,n,1);
}
}
}
int main(){
Solve();
return 0;
}
三、环形最大子段和
题目模型
- 把模型一的线性变成环形。有一个修改,不允许区间为空。
问题分析
方法一:
-
环形数组的连续最大子段和,有两种情况。
- 最大和的这个子段没有包含头尾。此时跟线型一样。
- 定义
dp[i]表示以a[i]结尾的最大子段和。 - 转移方程:
dp[i]=max(dp[i-1]+a[i],a[i])。
- 定义
- 最大和的这个子段包含了头尾。
- 此时:最大子段和 = 整个序列和 - 最小子段和。
- 此时最小子段和肯定是不包括头尾的,我们可以把原序列的每个元素乘以
-1,然后求出最大子段和,即为原序列的不包括头、尾的最小子段和。
- 最大和的这个子段没有包含头尾。此时跟线型一样。
-
然后比较两种情况的大小,输出大的那一个就行。
-
Code#include <bits/stdc++.h> const int maxn = 1e7+5,Inf=0x3f3f3f3f; typedef long long LL; LL a[maxn],b[maxn],dp[maxn]; LL sum = 0,Max = 0,Min = 0; void Solve(){ int n;scanf("%d",&n); srand(time(0));//随机种子 for(int i=1;i<=n;++i){ a[i]=rand()%10000-5000;//产生-5000~5000的随机数 b[i]=-a[i];//原序列元素乘-1 sum+=a[i];//序列之和 } for(int i=1;i<=n;++i){//对应情况1 dp[i]=std::max(dp[i-1]+a[i],a[i]); Max=std::max(Max,dp[i]); } memset(dp,0,sizeof(dp)); for(int i=1;i<=n;++i){//对应情况2,求b的最大子段和,取反后为a的的最小子段和 dp[i]=std::max(dp[i-1]+b[i],b[i]); Min=std::max(Min,dp[i]); } LL ans=std::max(Max,sum+Min);//sum+Min相当于序列和减去最小区间和 printf("%lld\n",ans); } int main(){ Solve(); return 0; }
方法二:
- 可以用单调队列,具体做法见下一个模型。
四、带长度限制的最大子段和
题目模型
- 一个整数序列\(a_1,a_2,……,a_n\) ,求最大的长度不超过
K的子段的数值和。
问题分析
-
求以
a[i]结尾的最大子段和,我们需要维护一个最小的前缀sum[j],即[j+1,i]为所求。 -
但要求子段和区间长度不能大于
K,则需要满足:i-j<=k。 -
如果
j'>j且sum[j']<sum[j],显然sum[j]对后面的求解就没有用了,所以我们可以用一个单调队列维护最远不超过K的最小前缀和。 -
Code#include <bits/stdc++.h> const int maxn = 1e5+5,Inf=0x3f3f3f3f; typedef long long LL; int a[maxn<<1],sum[maxn<<1]; void Solve(){ int n,k; scanf("%d%d",&n,&k); for(int i=1;i<=n;++i){ scanf("%d",&a[i]); sum[i]=sum[i-1]+a[i];//前缀和 } int ans=-Inf,l,r;//l:记录答案左边界,r:记录右边界 std::deque<int> q;//双端队列维护的 for(int i=1;i<=n;++i){ //因为区间[l,r]和为sum[r]-sum[l-1]所以要维护最小的sum[l-1] while(!q.empty() && sum[i-1]<sum[q.back()]) q.pop_back(); //保证最远的左端点离i的距离不能超过k while(!q.empty() && i-q.front()>k) q.pop_front(); q.push_back(i-1);//当前队列要么为空,要么队尾前缀和小于su[i-1] if(sum[i]-sum[q.front()]>ans){ ans=sum[i]-sum[q.front()]; l=q.front()+1;//注意左边界要+1 r=i; } } printf("%d %d %d\n",ans,l,r); } int main(){ Solve(); return 0; } -
Code手摸双端队列版,建议大家手写队列#include <bits/stdc++.h> const int maxn = 1e5+5,Inf=0x3f3f3f3f; typedef long long LL; int a[maxn<<1],sum[maxn<<1],q[maxn<<1]; void Solve(){ int n,k; scanf("%d%d",&n,&k); for(int i=1;i<=n;++i){ scanf("%d",&a[i]); sum[i]=sum[i-1]+a[i]; } int ans=-Inf,l,r; int head=0,tail=0; for(int i=1;i<=n;++i){ while(head<tail && sum[i-1]<sum[q[tail-1]]) tail--; while(head<tail && i-q[head]>k) head++; q[tail++]=i-1;//tail指向队尾的后一个位置 if(sum[i]-sum[q[head]]>ans){ ans=sum[i]-sum[q[head]]; l=q[head]+1; r=i; } } printf("%d %d %d\n",ans,l,r); } int main(){ Solve(); return 0; } -
习题:HDU-3415
五、最大M子段和
题目模型
N个整数组成的序列 \(a_1,a_2,a_3,…,a_n\) ,将这N个数划分为互不相交的M个子段,并且这M个子段的和是最大的。
问题分析
-
方法一:
-
看到序列,我们首先要尝试用线性
dp去处理,线性dp经典状态定义:f[i][j],i一般表示序列的前i个元素,j表示限制,这里表示划分了j个不相交的子段,我们还需要对i进行进一步的定义,即是否包含第i项,因为对当前元素a[i]来说,要么单独成一个子段,要么和最后一个子段合并,所以必须包含第i个元素。 -
动态转移方程:
dp[i][j]=max(dp[i-1][j],dp[k][j-1])+a[i] (j-1<=k<i)。 -
Code#include <bits/stdc++.h> const int maxn = 1e3+5,Inf=0x3f3f3f3f; typedef long long LL; int a[maxn],dp[maxn][maxn]; void Solve(){ int n,m;scanf("%d%d",&n,&m); for(int i=1;i<=n;++i) scanf("%d",&a[i]); for(int i=1;i<=n;++i){//前i个元素 for(int j=1;j<=std::min(i,m);++j){//划分出j个子段 if(i==j)dp[i][j]=dp[i-1][j-1]+a[i];//显然 else{ int temp=dp[i-1][j];//把a[i]直接并到最后一子段 for(int k=j-1;k<i;++k)//枚举上一个状态的最后一个子段的右端点,a[i]单独作为一个子段 temp=std::max(temp,dp[k][j-1]); dp[i][j]=temp+a[i]; } } } int ans=-Inf; for(int i=m;i<=n;++i) ans=std::max(ans,dp[i][m]); printf("%d\n",ans); } int main(){ Solve(); return 0; } -
时间效率为:\(O(n^3)\) ,空间效率为:\(O(m*n)\)。
-
-
方法二:
-
我们尝试对方法一的
dp阶段和状态进行修改, 即把子段限制数M作为阶段,即状态dp[i][j]表示把序列前j分成i个子段且包含a[j]的最大子段和。 -
动态转移方程有:
dp[i][j]=max(dp[i][j-1],dp[i-1][k])+a[j] (i-1<=k<j)。-
dp[i][j-1]+a[i]:表示合并到最后一个子段里 -
dp[i-1][k]+a[i]:表示前k元素挑出k个子段,所以k>=j-1,然后a[i]单独的子段。 -
此动态转移方程同样满足无后效性和最优子结构。
-
我们把问题的所有状态记录下来形成一个二维矩阵,显然当前状态只跟它上一行和左边的状态有关,我们可以把空间效率压掉以为变成 \(O(n)\) 。
-
同时上一行的状态只有在当前状态前面的最大值对转移有用,我们可以在遍历当前行时维护一下上一行的最大值,这样时间效率就压掉了一个
n,变成\(O(n*m)\)。 -
Code#include <bits/stdc++.h> typedef long long LL; const int maxn = 1e6+5; const LL Inf=0x3f3f3f3f3f3f3f3f; LL a[maxn],dp[2][maxn]; void Solve(){ int n,m;scanf("%d%d",&n,&m); for(int i=1;i<=n;++i) scanf("%lld",&a[i]); int k=1;//滚动数组指针,k表示当前行,!k表示上一行 for(int i=1;i<=m;++i,k=!k){//枚举区间个数 LL Max=-Inf; for(int j=i;j<=n;j++){ Max=std::max(Max,dp[!k][j-1]);//记录前j-1,分成i-1个区间时最大值 if(i==j) dp[k][j]=dp[!k][j-1]+a[j]; else//要么是a[j]单独成一个区间,此时为Max+a[j],或者直接合并为dp[k][j-1]+a[j] dp[k][j]=std::max(Max,dp[k][j-1])+a[j]; } } LL ans=-Inf; for(int i=m;i<=n;++i)//!k行才记录的是第m行的状态 ans=std::max(ans,dp[!k][i]); printf("%lld\n",ans); } int main(){ Solve(); return 0; }
-
-
六、可交换的最大子段和
题目模型
- \(n\) 个整数组成的序列\(a_1,a_2,...,a_n\),你可以对数组中的一对元素进行交换,并且交换后求 \(a_1\) 至 \(a_n\) 的最大子段和,所能得到的结果是所有交换中最大的。当所给的整数均为负数时和为
0。 - 例如:\(\{-2,11,-4,13,-5,-2, 4\}\)将
-4和4交换,\(\{-2,11,4,13,-5,-2, -4\}\),最大子段和为11 + 4 + 13 = 28。
问题分析
-
先说错误的做法,不少同学直接搬运了网上的题解,并完美的
ac了这道题,说句实话我是看了半天才明白其做法,对于最关键的地方一句显然,让人实在是无法理解。附上这些搬运工们的题解链接 -
做法的核心就是:显然sum[r]应该越大越好,就这么一句话就把枚举区间的时间效率由\(O(n^2)\)降到了\(O(n)\)。但这个显然没有找到一个合理的证明,还好找到了一组数据能够证明其错误,下面就附上错误做法和数据。
-
错误
Code#include <iostream> #include <cstdlib> #include <cstdio> #define inf 0x3f3f3f3f3f3f3f3f using namespace std; typedef long long ll; ///formula : sum[r] - sum[l - 1] - min[l,r] + max(max[1,l - 1],max[r + 1,n]) int n; ll sum[50005]; int s[50005]; int lmax[50005],rmax[50005]; int main() { while(~scanf("%d",&n)) { for(int i = 1;i <= n;i ++) { scanf("%d",&s[i]); sum[i] = sum[i - 1] + s[i]; } for(int i = 0;i < n;i ++) { lmax[i + 1] = max(lmax[i],s[i + 1]); rmax[n - i] = max(rmax[n - i + 1],s[n - i]); } int maxi = n; ll sumr_min,ans = 0; for(int i = n;i >= 1;i --) { if(sum[i] >= sum[maxi]) { maxi = i; sumr_min = sum[i] - s[i]; } sumr_min = max(sumr_min,sum[maxi] - s[i]); ans = max(ans,sumr_min - sum[i - 1] + max(lmax[i - 1],rmax[maxi + 1])); } printf("%lld\n",ans); } return 0; } /* input 10 1 -100 1 100 100 100 -1000 2 3 4 output 311 */ -
希望盲目
copy的同学们引以为戒,可以借鉴,但一定要理解,不然就会闹出大笑话了! -
正确做法:,任然是错误做法 -
这个车翻的有点猝不及防,才义正言辞的批评了一通 \(\Uparrow\) ,这个报应来得太快了,还好,代码是我写的,我只是没脑子(……),同学们头脑在线,这个老姚很欣慰!
-
交换操作,有以下三种情况:
- 被交换的两个数都在最大子段中;
- 被交换的两个数都不在最大子段中;
- 被交换的两个数只有一个在最大子段中;
-
显然,情况
1,2交换后不影响最大子段和结果,所以我们只需考虑情况3。 -
对情况
3,子段外的被交换的元素也有两种情况。- 被交换数在子段的左侧;
- 被交换数在子段的右侧;
-
假设 \(a_i\) 是最大子段和中需要交换的元素,我们需要从子段左侧去找一个最大数,最大数好找,我们只需预处理出,\(O(1)\)的效率就能找到,关键是如何找到子段的左边界。
-
对情况
1,如果我们能求出包含 \(a_{i-1}\) 最大后缀和,然后把 \(a_i\) 追加到后面即可,我们有多种方法\(O(n)\) 的预处理出结果和包含 \(a_{i-1}\) 的后缀的左边界,这样就确定了区间的左边界,然后再左边界左边找到最大的元素和啊\(a_i\) 进行交换即可。 -
对情况
2,同上面类似,如果我们能求出包含 \(a_{i+1}\) 最大前缀和,右边界,这样就确定了区间的右边界,然后再右边界右边找到最大的元素和啊\(a_i\) 进行交换即可。 -
然后从这两种情况中去较大者。
-
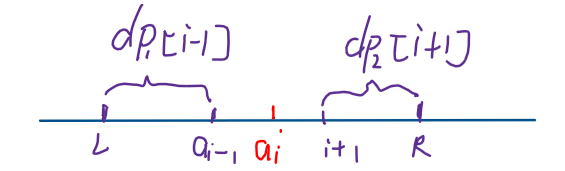
如下图,\(dp_1[i-1]\) 以\(a_{i-1}\) 结尾的最大子段和,\(L\)是其左边界,\(dp_2[i+1]\)表示以\(a_{i+1}\)开始的最大子段和,\(R\) 是其右边界。所以我们只需从 区间\([1,L)\),或区间\((R,n]\)找到最大的和 \(a_i\) 交换即可。
-
-
错误
Code#include <bits/stdc++.h> typedef long long LL; const int maxn = 5e4+5; const LL Inf=0x3f3f3f3f3f3f3f3f; LL a[maxn],dp1[maxn],dp2[maxn];//dp1[i]以a[i]结尾的最大子段和,dp2[i]表示以a[i]开始的最大子段和 LL L[maxn],R[maxn],Lmax[maxn],Rmax[maxn];//L[i]以a[i]结尾的最大子段和的左边界,R[i]类似。 void Solve(){ int n;scanf("%d",&n); for(int i=0;i<=n;++i)//Lmax[i]表示1~i的最大值,Rmax[i]表示i~n的最大值。 Lmax[i]=Rmax[i]=-Inf; for(int i=1;i<=n;++i){ scanf("%lld",&a[i]); Lmax[i]=std::max(a[i],Lmax[i-1]); if(dp1[i-1]+a[i]>0){//存在包含a[i]的结果为正的子段和 dp1[i]=dp1[i-1]+a[i]; if(dp1[i-1]==0)L[i]=i;//只选a[i]自己 else L[i]=L[i-1];//a[i]并到以a[i-1]结尾的最大子段中 } else L[i]=-1;//dp1[i-1]+a[i]<=0就什么都不选,为空 } Rmax[n+1]=-Inf; //如果a[n]为负,如果Rmax[n+1]=0,那求出的Rmax[n]=0,是错误的。 for(int i=n;i>0;--i){//倒序求以a[i]开始的最大子段和 Rmax[i]=std::max(a[i],Rmax[i+1]); if(dp2[i+1]+a[i]>0){ dp2[i]=dp2[i+1]+a[i]; if(dp2[i+1]==0)R[i]=i; else R[i]=R[i+1]; } else R[i]=-1; } LL ans=0; L[0]=R[n+1]=-1;//0不存在左边界,n+1不存在右边界 for(int i=1;i<=n;++i){ LL x=0; int l=i,r=i;//l,r记录区间的左右边界 if(L[i-1]!=-1){x+=dp1[i-1];l=L[i-1];}//如果存在以a[i-1]结尾的大于0最大子段和 if(R[i+1]!=-1){x+=dp2[i+1];r=R[i+1];}//如果存在以a[i+1]开始的大于0最大子段和 ans=std::max(ans,x+std::max(Lmax[l-1],Rmax[r+1])); } printf("%lld\n",ans); } int main(){ Solve(); return 0; } /* 4 -2 -4 1 -1 上面代码过不了下面的样例 错误的愿因是需要交换的a[i]向左扩展并不一定是包含a[i-1]的最大子段和 6 100 -1 1 -10 1 1 */




