树链剖分
树链剖分
1. 相关概念
-
重儿子:父亲节点的所有儿子中子树结点数目最多(
size最大)的结点; -
轻儿子:父亲节点中除了重儿子以外的儿子;
-
重边:父亲结点和重儿子连成的边;
-
轻边:父亲节点和轻儿子连成的边;
-
重链:由多条重边连接而成的路径;
-
轻链:由多条轻边连接而成的路径
-
如下图所示
-
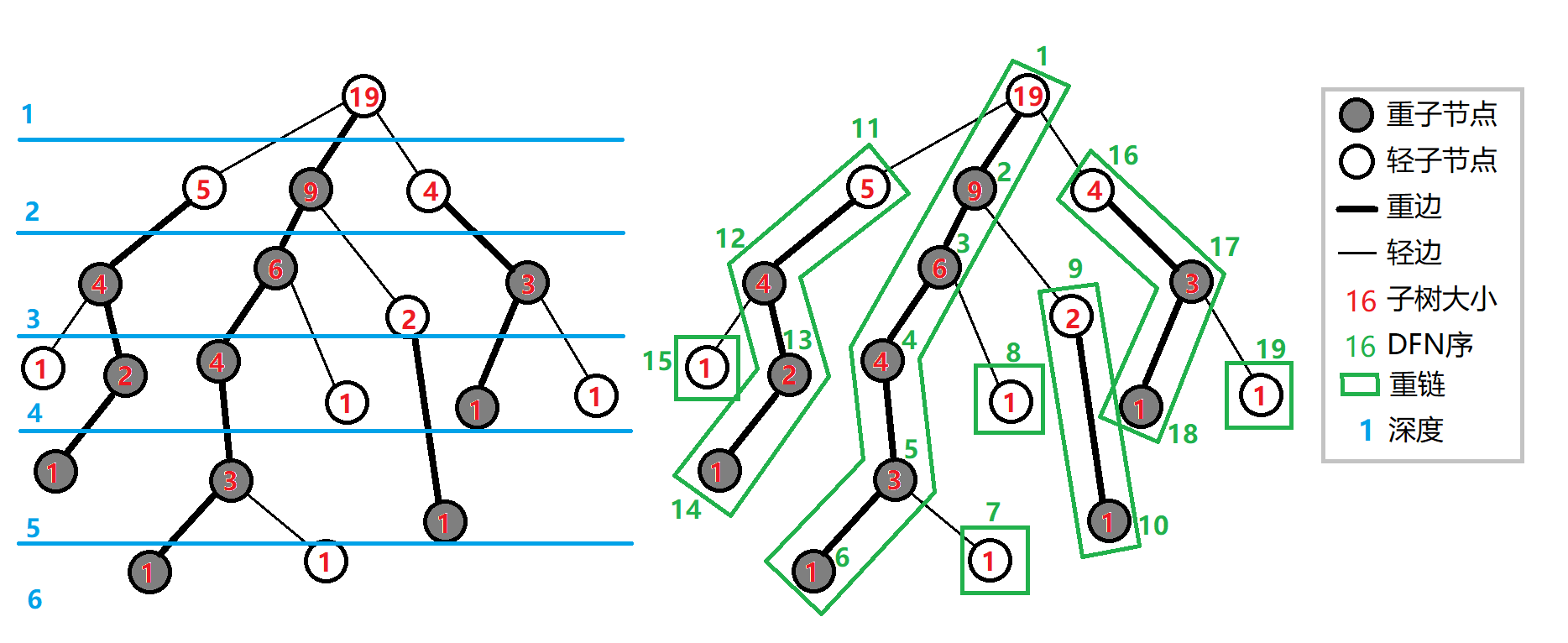
2. 树链剖分的实现
-
- 上图,红点为重链的起点,加粗黑边为重边,细边为轻边,加粗黑圈为重子节点,其他为轻子节点,节点右边的数字为第二遍
dfs遍历顺序。
- 上图,红点为重链的起点,加粗黑边为重边,细边为轻边,加粗黑圈为重子节点,其他为轻子节点,节点右边的数字为第二遍
-
首先求出每个节点所在的子树大小,找到它的重儿子(即预处理出
size,son数组)- 比如:节点
1的三个子节点,size[2]=5,size[3]=2,size[4]=6,节点最大的是4,所以,节点1的重儿子是节点4。 - 如果一个节点的多个子节点一样大,且均为最大节点,那随便找一个当做它的重儿子。
- 叶节点没有重儿子,非叶节点有且只有一个重儿子。
- 比如:节点
-
在
dfs过程中顺便记录其父亲以及深度,操作1,2可以通过一遍dfs完成。void dfs1(int u,int fa){ //预处理出当前节点、父节点、层次深度 f[u]=fa;size[u]=1; //这个点本身size=1 for(int i=head[u];i;i=e[i].next){ int v=e[i].to; if(v==fa)continue; deep[v]=deep[u]+1; dfs1(v,u); //层次深度+1 size[u]+=size[v]; //子节点的size已被处理,用它来更新父节点的size if(size[v]>size[son[u]])//选取size最大的作为重儿子 son[u]=v; //son[u]表示u的重儿子 } } -
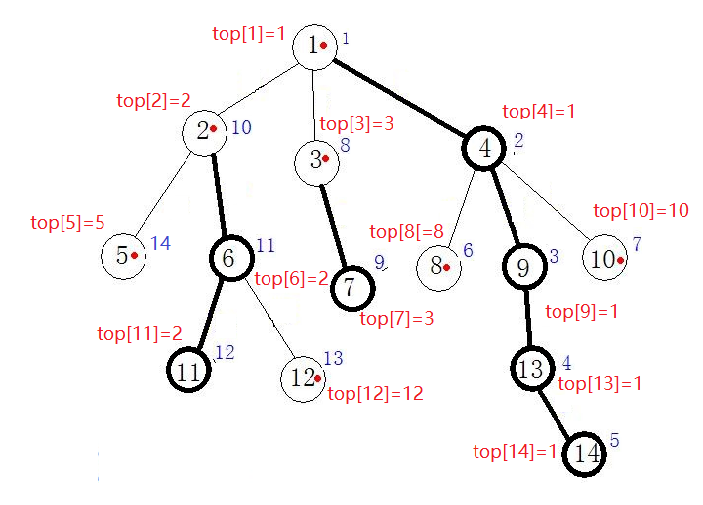
第二遍
dfs,连接重链,同时标记每一个节点的dfs序,并且为了用数据结构来维护重链,我们在dfs时保证一条重链上各个节点dfs序连续。void dfs2(int u,int t){ //当前节点、重链顶端 top[u]=t;//保存当前节点所在链的顶端节点 dfn[u]=++cnt; //cnt标记dfs序 rk[cnt]=u; //序号cnt对应节点u if(son[u])dfs2(son[u],t);//先走重儿子 /*我们选择优先进入重儿子来保证一条重链上各个节点dfs序连续, 一个点和它的重儿子处于同一条重链,所以重儿子所在重链的顶端还是t*/ for(int i=head[u];i;i=e[i].next){//遍历轻链 int v=e[i].to; if(v!=son[u]&&v!=f[u]) dfs2(v,v); //一个点位于轻链底端,那么它的top必然是它本身 } }
3. 树链刨分LCA
-
算法实现:求树上节点
u,v的LCA。- 如果
u,v在同一个重链上,即,top[u]==top[v],则深度小的为LCA。 - 节点
u,v不在同一个重链,让深度大的链顶节点u往上跳,跳到其链顶的父亲节点上,即u=f[top[u]]. - 重复步骤
2直到节点u,v在同一个重链,此时深度小的为LCA。
- 如果
-
例题:
luogu P3379树链剖分求LCA -
Code#include <bits/stdc++.h> const int maxn=5e5+5; struct edge{ int to,next; }e[2*maxn]; int n,m,root,len,head[maxn],deep[maxn],siz[maxn],son[maxn],top[maxn],f[maxn]; void Insert(int x,int y){ e[++len].to=y;e[len].next=head[x];head[x]=len; } void dfs1(int u){ siz[u]=1;deep[u]=deep[f[u]]+1; for(int i=head[u];i;i=e[i].next){ int v=e[i].to; if(v==f[u])continue; f[v]=u; dfs1(v); siz[u]+=siz[v]; if(!son[u]||siz[son[u]]<siz[v])//求重儿子 son[u]=v; } } void dfs2(int u,int tp){ top[u]=tp; if(son[u])dfs2(son[u],tp); for(int i=head[u];i;i=e[i].next){ int v=e[i].to; if(v!=f[u] && v!=son[u])//v是轻儿子 dfs2(v,v); } } int LCA(int u,int v){ while(top[u]!=top[v]){ if(deep[top[u]]>=deep[top[v]]) u=f[top[u]]; else v=f[top[v]]; } return deep[u] < deep[v] ? u : v; } void Solve(){ scanf("%d%d%d",&n,&m,&root); for(int i=1;i<n;++i){ int x,y;scanf("%d%d",&x,&y); Insert(x,y);Insert(y,x); } dfs1(root); dfs2(root,root); for(int i=1;i<=m;++i){ int u,v;scanf("%d%d",&u,&v); printf("%d\n",LCA(u,v)); } } int main(){ Solve(); return 0; } -
时间效率:
dfs为O(n),查询一次为:O(log(n)),总的时间效率:O(m*log(n))。 -
当
u,v均在轻链的底端是,每次往上跳时只能从父亲节点一个个往上跳,但轻链到根节点距离小于log(n),一般情况下树链刨分的常数非常小,不到1/2。
树链剖分(线段树)
-
例题:
luogu P3384【模板】轻重链剖分 -
分析:
-
区间修改、区间查询是线段树的基本操作,但我们熟悉的是线性数据结果上的操作。
-
树链剖分正好能把树上的路径划分成一条条重链,一条重链正好是一个区间。
-
Code#include<bits/stdc++.h> using namespace std; const int maxn=1e5+1000; struct edge{int next,to;}e[maxn<<2]; struct node{int l,r,w,siz,lazy;}tr[maxn<<2]; int len,root,MOD,cnt=0,n,m; int a[maxn],head[maxn];; int deep[maxn],f[maxn],son[maxn],size[maxn],top[maxn],dnf[maxn],rk[maxn]; void Insert(int u,int v){ e[++len].to=v;e[len].next=head[u];head[u]=len; } void dfs1(int u,int fa){//处理深度,父亲节点,u为根的节点个数 size[u]=1; for(int i=head[u];~i;i=e[i].next){ int v=e[i].to; if(v==fa) continue; deep[v]=deep[u]+1;f[v]=u; dfs1(v,u); size[u]+=size[v]; if(!son[u] || size[v]>size[son[u]])//重链的儿子 son[u]=v; } } void dfs2(int u,int tp){ top[u]=tp;//标记重链的顶点 dnf[u]= ++cnt;//节点对应编号 rk[cnt]=a[u];//编号对应节点建树的关键一员 if(son[u]) dfs2(son[u],tp); for(int i=head[u];~i;i=e[i].next){ int v=e[i].to; if(v!=son[u] && v!=f[u]) dfs2(v,v);//非重链的顶点就是自己 } } void push_up(int u){ tr[u].w=(tr[u<<1].w+tr[u<<1|1].w+MOD)%MOD; } void build(int u,int l,int r){ tr[u].l=l;tr[u].r=r;tr[u].siz=r-l+1; if(l==r){ tr[u].w=rk[l]; return ; } int mid=(l+r)>>1; build(u<<1,l,mid);build(u<<1|1,mid+1,r); push_up(u); } void push_down(int u){ if(tr[u].lazy){ tr[u<<1].w=(tr[u<<1].w+tr[u<<1].siz*tr[u].lazy)%MOD; tr[u<<1|1].w=(tr[u<<1|1].w+tr[u<<1|1].siz*tr[u].lazy)%MOD; tr[u<<1].lazy=(tr[u<<1].lazy+tr[u].lazy)%MOD; tr[u<<1|1].lazy=(tr[u<<1|1].lazy+tr[u].lazy)%MOD; tr[u].lazy=0; } } void update(int u,int l,int r,int val){ if(l<=tr[u].l && tr[u].r<=r){ tr[u].w+=tr[u].siz*val; tr[u].lazy+=val; return ; } push_down(u); int mid=(tr[u].l+tr[u].r)>>1; if(l<=mid) update(u<<1,l,r,val); if(r>mid) update(u<<1|1,l,r,val); push_up(u); } void treeadd(int u,int v,int val){ while(top[u]!=top[v]){//将两个节点跳到同一重链上 if(deep[top[u]]<deep[top[v]]) swap(u,v); update(1,dnf[top[u]],dnf[u],val); u=f[top[u]]; } if(deep[u]>deep[v]) swap(u,v);//节点编号的顺序依照深度大小,深度越大节点编号越大 update(1,dnf[u],dnf[v],val);//因为遍历线段树区间[l,r]必须从小到大 } int query(int u,int l,int r){ int ans=0; if(l<=tr[u].l && tr[u].r<=r) return tr[u].w; push_down(u); int mid=(tr[u].l+tr[u].r)>>1; if(l<=mid) ans=(ans+query(u<<1,l,r))%MOD; if(r>mid) ans=( ans+query(u<<1|1,l,r))%MOD; return ans; } void querysum(int u,int v){//树剖求区间和 int ans=0; while(top[u]!=top[v]){//不在一条重链上时,把深度低的链顶到节点连续区间求和 if(deep[top[u]]<deep[top[v]]) swap(u,v); ans=(ans+query(1,dnf[top[u]],dnf[u]))%MOD; u=f[top[u]]; }//跳出循环后,u,v在同一条链 if(deep[u]>deep[v]) swap(u,v); ans=(ans+query(1,dnf[u],dnf[v]))%MOD; printf("%d\n",ans); } int main(){ memset(head,-1,sizeof(head)); scanf("%d%d%d%d",&n,&m,&root,&MOD); for(int i=1;i<=n;i++) scanf("%d",&a[i]); for(int i=1;i<=n-1;i++){ int x,y; scanf("%d %d",&x,&y); Insert(x,y);Insert(y,x); } dfs1(root,0); dfs2(root,root); build(1,1,n); while(m--){ int op,x,y,z; scanf("%d",&op); if(op==1){ scanf("%d%d%d",&x,&y,&z); z=z%MOD; treeadd(x,y,z); } else if(op==2){ scanf("%d %d",&x,&y); querysum(x,y); } else if(op==3){ scanf("%d %d",&x,&y); update(1,dnf[x],size[x]+dnf[x]-1,y%MOD); } else if(op==4){ scanf("%d",&x); printf("%d\n",query(1,dnf[x],dnf[x]+size[x]-1)); } } }
-
hzoi




