带权二分图最大匹配KM算法

二分图的判定

• 如果一个图是连通的，可以用如下的染色法判定是否二分图：

  • 我们把X部的结点颜色设为0，Y部的颜色设为1。

  • 从某个未染色的结点u开始，做BFS或者DFS 。把u染为0，枚举u的儿子v。如果v未染色，就染为与u相反的颜色，如果已染色，则判断u与v的颜色是否相同，相同则不是二分图。

  • 如果一个图不连通，则在每个连通块中作判定。

    #include <bits/stdc++.h>
    const int maxn = 505;
    std::vector<int> e[maxn];
    int m,n,color[maxn];
    bool flag;//全局，标记是否有环
    void dfs(int u){
        if(flag) return;//如果已经存在环就没必要接着递归了
        int len = e[u].size();//省点常数
        for(int i = 0; i < len; i++){    //遍历所有相邻顶点，即连着的点
        	int v = e[u][i];
            if(color[v]==0){//v还未访问，染色并递归
            	color[v] = -color[u];
            	dfs(v);
            }
            else if(color[v]==color[u]){
            	flag=1;//说明有环
            	return;
            }
        }
    }
     
    void solve(){
        for(int i = 0; i < n; i++){
            if(color[i] == 0){
            	color[i] = 1;
                dfs(i);
                if(flag){
                	printf("NOT BICOLORABLE.\n");
                    return;
                }                
            }
        }
        printf("BICOLORABLE.\n");
    } 
    int main(){
        while(~scanf("%d%d",&n,&m)){
            memset(color, 0, sizeof(color));
            memset(e, 0, sizeof(e));
            for(int i = 0; i < m; i++){
                int u,v;scanf("%d%d",&u,&v);    
                e[u].push_back(v);e[v].push_back(u);
            }
            solve();
        }
        return 0;
    }
    

最大匹配KM算法

• 顶标：设顶点 \(X_i\) 的顶标为 \(A[i]\)，顶点 \(Y_j\) 的顶标为 \(B[j]\) ，顶点 \(X_i\) 与 \(Y_j\) 之间的边权为 \(w[i][j]\)，初始化时，\(A[i]\) 的值为与该点关联的最大边权值，\(B[j]\) 的值为0

• 相等子图：选择 \(A[i] + B[j] = w[i][j]\) 的边 \(<i, j>\) 构成的子图，就是相等子图。

• 算法执行过程中，对任一条边\(<i, j>\) ，\(A[i] + B[j] >= w[i][j]\) 恒成立。

• slack数组存的数是Y部的点相等子图时，最小要增加的值

• 算法图示：

  1. 从\(X_1\) 开始跑匈牙利，匹配的条件是：\(A[i] + B[j] = w[i][j]\) ，显然 $ X_1$ 和 \(Y_3\) 匹配成功。

     

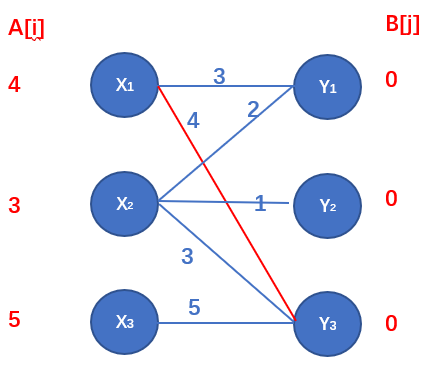
  2. 接着从 \(X_2\) 开始，\(A[X_2]+B[Y_3]==w[X_2][X_3]\) ，此时 \(Y_3\) 已被 \(X_1\) 匹配，尝试让 \(X_1\) 换一个匹配对象，但在 \(X_1\) 的邻接点没有满足：\(A[i] + B[j] = w[i][j]\) 的点，这些相临边和顶标和的最小差值为：\(minz=1\) ，把此时已标记的 \(X\) 部的顶标减去\(minz\)，即：\(A[x_1]=5-1=4,A[X_2]-1=3\) ， \(Y\) 部的此时标记的顶标加上\(minz\)，即：\(B[y_3]=0+1=1\) ，此时\(A[X_1]+B[Y_1]==w[X_1][Y_1]\)。

     

  3. 最后从\(X_3\) 开始找增广路，\(X_3\) 匹配 \(Y_3\) ，不满足，调整顶标，即\(A[3]=5-1=4\)，匹配\(Y_3\) 成功，尝试劝说 \(X_2\) 寻找新的匹配，此时 \(Y_1\) 满足匹配，尝试让 \(X_1\) 寻找新的匹配，此时\(X_1\)已找不到新的为匹配的点，匹配失败，回溯到 \(X_2\) ，
     

• Code

  #include <bits/stdc++.h>
  const int maxn = 300 + 10,maxe=1e4+5,Inf = 0x3f3f3f3f;
  struct Edee{int to,w,next;}e[maxe];
  int n,m,len,head[maxn],g[maxn][maxn];
  int wx[maxn], wy[maxn];//每个点的顶标值（需要根据二分图处理出来）
  int match[maxn];//每个Y部点所匹配的X部的点
  int visx[maxn], visy[maxn];//每个点是否加入增广路
  int slack[maxn];//边权和顶标最小的差值
  void Insert(int u,int v){
  	e[++len].to=v;e[len].next=head[u];head[u]=len;
  }
  bool dfs(int u){//进入DFS的都是X部的点，找到增光路返回1，否则返回0
      visx[u] = 1;//标记进入增广路    
      for(int i = head[u]; i ; i=e[i].next){
      	int v = e[i].to;
          if(!visy[v]){//如果Y部的点还没进入增广路,并且存在路径        
              int t = wx[u] + wy[v] - g[u][v];
              if(t == 0){//t为0说明是相等子图            
                  visy[v] = 1;//加入增广路                
                  if(match[v] == -1 || dfs(match[v])){                    
                      match[v] = u;//进行匹配
                      return 1;
                  }
              }
              else if(t > 0)//此处t一定是大于0，因为顶标之和一定>=边权
                  slack[v] = std::min(slack[v], t);
                  //slack[v]存的是Y部的点需要变成相等子图顶标值最小增加多少
          }
      }
      return false;
  }
  
  int KM(){
      memset(match, -1, sizeof(match));
      memset(wx, 0, sizeof(wx));//wx的顶标为该点连接的边的最大权值
      memset(wy, 0, sizeof(wy));//wy的顶标为0
      for(int u = 1; u <= n; u++){//预处理出顶标值    
          for(int i = head[u]; i ; i=e[i].next)
              wx[u] = std::max(wx[u], g[u][e[i].to]);
      }
      for(int i = 1; i <= n; i++){//枚举X部的点    
          memset(slack, 0x3f, sizeof(slack));
          while(1){
              memset(visx, 0, sizeof(visx));
              memset(visy, 0, sizeof(visy));
              if(dfs(i))break;//已经匹配正确
              int minz = Inf;
              for(int j = 1; j <= n; j++)
                  if(!visy[j] && minz > slack[j])                    
                      minz = slack[j];//找出还没经过的点中，需要变成相等子图的最小额外增加的顶标值          
              //将X部已访问的顶标减去minz，Y部已访问的顶标加上minz
              for(int j = 1; j <= n; j++)
                  if(visx[j])wx[j] -= minz;
              for(int j = 1; j <= n; j++)
                  //修改顶标后，要把所有不在交错树中的Y顶点的slack值都减去minz
                  if(visy[j])wy[j] += minz;
                  else slack[j] -= minz;//未在增光路，但相应的X部已访问的顶标减少了,其相邻的未访问的期望也减小
          }
      }
  
      int ans = 0;//二分图最优匹配权值
      for(int i = 1; i <= n; i++)
          if(match[i] != -1)ans += g[match[i]][i];
      return ans;
  }
  int main(){
      while(scanf("%d%d", &n,&m) != EOF){
          for(int i = 1; i <= m; i++){
              int u,v,w;scanf("%d%d%d", &u,&v,&w);
              g[u][v]=w;Insert(u,v);
          }
          printf("%d\n", KM());
      }
      return 0;
  }