二分图

概念
- 二分图：把一个图的顶点划分为两个不相交集 U 和V ，使得每一条边都分别连接U、V中的顶点。如果存在这样的划分，则此图为一个二分图。二分图的一个等价定义是：不含有「含奇数条边的环」的图。图 1 是一个二分图。为了清晰，我们以后都把它画成图 2 的形式。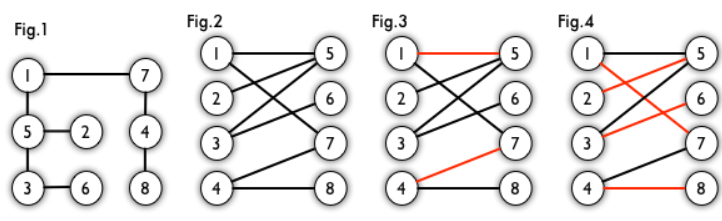
- 匹配：在图论中，一个「匹配」（matching）是一个边的集合，其中任意两条边都没有公共顶点。例如，图 3、图 4 中红色的边就是图 2 的匹配。
- 我们定义匹配点、匹配边、未匹配点、非匹配边，它们的含义非常显然。例如图 3 中 1、4、5、7 为匹配点，其他顶点为未匹配点；(1,5)、(4,7)为匹配边，其他边为非匹配边。
- 最大匹配：一个图所有匹配中，所含匹配边数最多的匹配，称为这个图的最大匹配。图 4 是一个最大匹配，它包含 4 条匹配边。
- 完美匹配：如果一个图的某个匹配中，所有的顶点都是匹配点，那么它就是一个完美匹配。图 4 是一个完美匹配。显然，完美匹配一定是最大匹配（完美匹配的任何一个点都已经匹配，添加一条新的匹配边一定会与已有的匹配边冲突）。但并非每个图都存在完美匹配。
- 举例来说：如下图所示，如果在某一对男孩和女孩之间存在相连的边，就意味着他们彼此喜欢。是否可能让所有男孩和女孩两两配对，使得每对儿都互相喜欢呢？图论中，这就是完美匹配问题。如果换一个说法：最多有多少互相喜欢的男孩/女孩可以配对儿？这就是最大匹配问题。
匈牙利算法，求解最大匹配问题的一个算法是匈牙利算法
- 交替路：从一个未匹配点出发，依次经过非匹配边、匹配边、非匹配边…形成的路径叫交替路。如图5 中\(9\rightarrow 4\rightarrow 8\rightarrow 1\rightarrow 6\rightarrow 2\) 就是一条交替路。
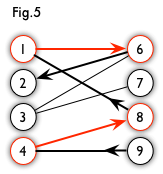
- 增广路：从一个未匹配点出发，走交替路，如果途径另一个未匹配点（出发的点不算），则这条交替路称为增广路（agumenting path）。例如，图 5 中的一条增广路如图 6 所示（图中的匹配点均用红色标出）：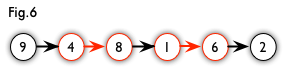
  - 增广路有一个重要特点：非匹配边比匹配边多一条。因此，研究增广路的意义是改进匹配。
  - 只要把增广路中的匹配边和非匹配边的身份交换即可。
  - 由于中间的匹配节点不存在其他相连的匹配边，所以这样做不会破坏匹配的性质。
  - 交换后，图中的匹配边数目比原来多了 1 条。
  - 我们可以通过不停地找增广路来增加匹配中的匹配边和匹配点。找不到增广路时，达到最大匹配（这是增广路定理）。匈牙利算法正是这么做的。在给出匈牙利算法 DFS 和 BFS 版本的代码之前，先讲一下匈牙利树。
- 匈牙利树：一般由 BFS 构造（类似于 BFS 树）。从一个未匹配点出发运行 BFS（唯一的限制是，必须走交替路），直到不能再扩展为止。例如，由图 7，可以得到如图 8 的一棵 BFS 树：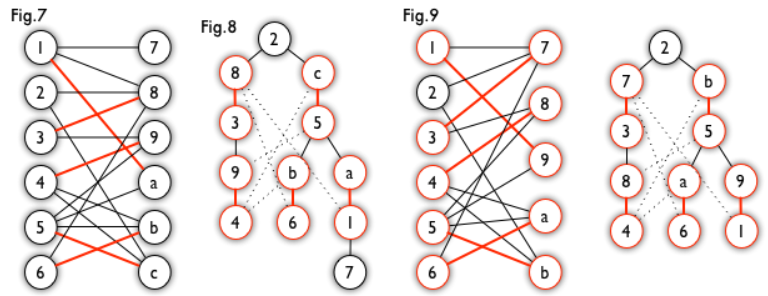
  - 这棵树存在一个叶子节点为非匹配点（7 号），但是匈牙利树要求所有叶子节点均为匹配点，因此这不是一棵匈牙利树。如果原图中根本不含 7 号节点，那么从 2 号节点出发就会得到一棵匈牙利树。这种情况如图 9 所示（顺便说一句，图 8 中根节点 2 到非匹配叶子节点 7 显然是一条增广路，沿这条增广路扩充后将得到一个完美匹配）。

例题：月老的难题

Description

月老准备给n个女孩与n个男孩牵红线，成就一对对美好的姻缘。

现在，由于一些原因，部分男孩与女孩可能结成幸福的一家，部分可能不会结成幸福的家庭。

现在已知哪些男孩与哪些女孩如果结婚的话，可以结成幸福的家庭，月老准备促成尽可能多的幸福家庭，请你帮他找出最多可能促成的幸福家庭数量吧。

假设男孩们分别编号为\(1\sim n\),女孩们也分别编号为 \(1\sim n\)。

Input

第一行是一个整数T,表示测试数据的组数(1<=T<=400)

每组测试数据的第一行有两个整数n,K，其中男孩的人数与女孩的人数都是n。(n<=500,K<=10 000)

随后的K行，每行有两个整数i,j表示第i个男孩与第j个女孩有可能结成幸福的家庭。(1<=i,j<=n)

Output

对每组测试数据，输出最多可能促成的幸福家庭数量

Sample Input
1
3 4
1 1
1 3
2 2
3 2
Sample Output
2
Code
#include <bits/stdc++.h>
const int maxn=505;
int vis[maxn];//访问标记数组，用来剪枝
std::vector<int> g[maxn];//vector数组用来充当邻接表
int girls[maxn];//女孩子的男朋友
int n;//标记匹配的男生或者是女生的人数
bool Find(int x){//匈牙利算法，参数x表示编号是x的男生找女朋友
    for(int i=0;i<g[x].size();i++){
        int y=g[x][i];//获取当前男生的每个女朋友
        if(vis[y]==0){//如果当前女生没有被访问过        
            vis[y]=1;//标记访问
            if(girls[y]==0||Find(girls[y])){//如果这个女生没有男朋友或者是递归查找这个女生的男朋友有备胎可以选择            
                girls[y]=x;//那么这个女生就给这个男生分配
                return true;//一旦分配了,相当于多了一对匹配了，就返回
            }
        }
    }
    return false;//如果最后也没有成功分配，那么就返回false
}
int main(){
    int T;scanf("%d",&T);
    while(T--){
        for(int i=0;i<maxn;i++)
            g[i].clear();//初始化每个男生的喜欢的女孩子的编号为空
        int m;scanf("%d%d",&n,&m);
        for(int i=0;i<m;i++){
            int v,u;scanf("%d%d",&u,&v);
            g[u].push_back(v);//u的心仪对象是v号女孩
        }
        memset(girls,0,sizeof(girls));//初始化所有女生的男朋友没有
        int ans=0;//男生匹配成功的数目为0
        for(int i=1;i<=n;i++){//遍历每一个男生        
            memset(vis,0,sizeof(vis));//每次深搜前都初始化所以的女生都没有被访问过
            if(Find(i))//如果当前男生成功被匹配
                ans++;//成功数目+1
        }
        printf("%d\n",ans);//输出最终的答案
    }
    return 0;
}

补充定义和定理：
- 最大匹配数：最大匹配的匹配边的数目
- 最小点覆盖数：选取最少的点，使任意一条边至少有一个端点被选择
- 最大独立数：选取最多的点，使任意所选两点均不相连
- 最小路径覆盖数：对于一个 DAG（有向无环图），选取最少条路径，使得每个顶点属于且仅属于一条路径。路径长可以为 0（即单个点）。
- 定理
  - 定理一：最大匹配数 = 最小点覆盖数（这是 Konig 定理）
  - 定理2：最大匹配数 = 最大独立数
  - 定理3：最小路径覆盖数 = 顶点数 - 最大匹配数

posted @ 2020-05-04 14:35 ♞老姚♘ 阅读(816) 评论(0) 编辑收藏举报

刷新页面返回顶部

hzoi_anby

二分图

二分图

Description

Input

Output

Sample Input

Sample Output

公告