差分约束

差分约束

1. 概念

  • 如果一个系统由n个变量和m个约束条件组成，形成m个形如\(a_i-a_j\le k\)的不等式(\(i,j\in [1,n],k\)为常数),则称其为差分约束系统。

2. 引例

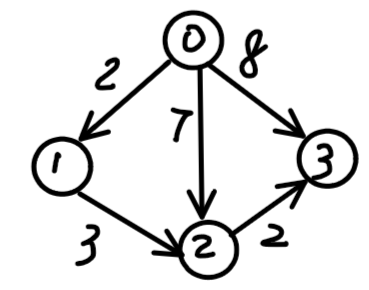
  • 给定n个变量和m个不等式，每个不等式形如\(x_i- x_j\le w\)，求\(x_{n-1}-x_0\) 的最大值。(0 <= i, j < n)

  • 例如n=4,m=5，有如下五个不等式：

    • \(x_1 - x_0\le 2\) ①
    • \(x_2 - x_0 \le7\) ②
    • \(x_3 - x_0\le 8\) ③
    • \(x_2 - x_1\le 3\) ④
    • \(x_3 - x_2\le 2\) ⑤

  • 对上面的五个不等式进行运算，我们能得到\(x_3-x_0\) 的三个不等式：

    1. ③ $ \Rightarrow x_3 - x_0\le 8$
    2. ② + ⑤ $ \Rightarrow x_3 - x_0\le 9$
    3. ① + ④ + ⑤ $ \Rightarrow x_3 - x_0\le 7$

  • 显然上面三个不等式都满足，则\(x_3-x_0=min(8,9,7)\) ，即\(x_3-x_0\) 最大为7。

  • 令\(x_3=d[v], x_0=d[u]\) 不等式右边的值为\(w(u,v)\) 表示u到v的距离，然后对上面三个不等式移项可得：

    • \(d[v]\le d[u]+w(u,v)\)
    • 对上面的式子大家是不是很熟悉，跟我们求最短路的松弛很相像！

  • 对上面的关系，如果\(x_1-x_0\le 2\)，则我们就建一条\(x_0\rightarrow x_1\) 权值为2的有向边，我们用下图来表示：

  • 对上图，如果我们要想求\(x_i- x_j\) 的最大值，我们只需求出\(x_j\rightarrow x_i\) 的最短路即可。

3. 问题解的存在性

  • 由于在求解最短路时会出现存在负环或者终点根本不可达的情况，在求解差分约束问题时同样存在
    1. 存在负环：如果路径中出现负环，就表示最短路可以无限小，即不存在最短路，那么在不等式上的表现即\(x_{n-1}-x_0 \le w\)中的 \(w\) 无限小，得出的结论就是 \(x_{n-1}-x_0\) 的最大值不存在。在SPFA实现过程中体现为某一点的入队次数大于节点数。
    2. 终点不可达：这种情况表明\(x_{n-1}\)和\(x_0\) 之间没有约束关系，\(x_{n-1}-x_0\) 的最大值无限大，即\(x_{n-1}\)和 \(x_n\) 的取值有无限多种。在代码实现过程中体现为\(dis[n-1]=INF\)。

4. 不等式组的转化

  • 做题时可能会遇到不等式中的符号不相同的情况，但我们可以对它们进行适当的转化：
    1. 方程给出：\(x_{n-1}-x_0\ge w\),可以进行移项转化为：\(x_0-x_{n-1}\le -w\)。
    2. 方程给出：\(x_{n-1}-x_0<w\), 可以转化为：\(x_{n-1}-x_0\le w-1\)。
    3. 方程给出：\(x_{n-1}-x_0 =w\)，可以转化为\(x_{n-1}-x_0\le w\ \&\&\ x_{n-1}-x_0 \ge w\)，再利用1.进行转化即可。

5. 应用

  • 对于不同的题目，给出的条件都不一样，我们首先需要关注问题是什么
    • 如果需要求的是两个变量差的最大值，那么需要将所有不等式转变成<=的形式，建图后求最短路；
    • 如果需要求的是两个变量差的最小值，那么需要将所有不等式转化成>=，建图后求最长路。

例题

  1. poj1716 Integer Intervals

    Description
    • 区间[a,b], a<b，表示包含a,b连续整数的集合，给出若干个类似的区间集合，我们从每个集合中至少挑出2个元素组成一个新的集合，求满足条件新集合最小元素个数。
    Input
    • 第一行有一个整数n\(1\le n\le 10000\);
    • 接下来n行，包含两个整数a,b(\(0\le a<b\le 10000\))，表示区间[a,b]。
    Output
    • 输出满足条件集合的最少元素个数。
    Sample Input
    4
3 6
2 4
0 2
4 7
    Sample Output
    4

    • 分析：

      • 令sum[x]为区间集合[0,x]中的被选中的元素个数。
      • 显然，区间集合[a,b]必须满足：sum[b+1]-sum[a]>=2
      • 隐含的约束条件：0<=sum[i+1]-sum[i]<=1，即单个元素的集合
      • 对上面的三个不等式我们统一格式可化为：
        • \(sum[b+1]-sum[a]>=2\) 建边：Insert(a,b+1,2)
        • \(sum[i+1]-sum[i]>=0\) 建边：Insert(i,i+1,0)
        • \(sum[i]-sum[i+1]>=-1\) 建边：Insert(i+1,i,-1)
      • 建边后跑个最长路即可。

    • 代码：

      //#include <bits/stdc++.h>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <queue>
const int maxn=1e4+5,Inf=0x3f3f3f3f;
struct node{int to,dis,next;} e[maxn*3];
int dis[maxn],vis[maxn],head[maxn];
int n,len; 
void Insert(int u,int v,int w){
    e[++len].to=v;e[len].dis=w;e[len].next=head[u];head[u]=len;
}
void spfa(int s,int t){
    for(int i=0;i<=t;i++){//初始化 
        dis[i]=-Inf;vis[i]=0;
    }
    std::queue<int>q;
	vis[s]=1;dis[s]=0;q.push(s);//起点入队 
    int cnt[maxn]={0};//cnt[i]表示节点i的进队次数，判正环用 
    cnt[s]++;
    while(!q.empty()){		
        int u=q.front();q.pop();vis[u]=0;        
        for(int i=head[u];i;i=e[i].next){
            int v=e[i].to, w=e[i].dis;
            if(dis[v]<dis[u]+w){
                dis[v]=dis[u]+w;
                if(!vis[v]){
                    vis[v]=1;q.push(v);cnt[v]++;
                    if(cnt[v]>t)return;//说明有正环 
                }
            }
        }
    }
}
void Solve(){
	while(~scanf("%d",&n)){
        len=0;memset(head,0,sizeof(head));//多组数据，注意初始化 
        int Max=0;//记录区间右边界的最大值 
        for(int i=0;i<n;i++){
            int a,b;scanf("%d%d",&a,&b);
            Insert(a,b+1,2);
            Max=std::max(Max,b+1);
        }
        for(int i=0;i<=Max;i++){//处理隐含条件 
            Insert(i,i+1,0);Insert(i+1,i,-1);
        }
        spfa(0,Max);
        printf("%d\n",dis[Max]);
    }
} 
int main(){   
    Solve(); 
    return 0;
}

  2. hdu 3666THE MATRIX PROBLEM

    Description
    • 给你一个\(M\times N\)的矩阵，矩阵元素为不超过1000的正数，问是否存在n个数的序列\(a_1,a_2,...,a_n\)，和m个数\(b_1,b_2,...,b_m\)，满足使第i行的每个元素乘以\(a_i\),第j列中的每个元素除以\(b_j\)之后，这个矩阵中的每个元素都在L和U之间，L表示元素的下界，U表示元素的上界。
    Input
    • 存在多组数据
    • 每组数据第一行有四个整数N,M,L,U(1<=N,M<=400,1<=L<=U<=10000)，接下来N行，每行M个整数，表示矩阵元素。
    Output
    • 如果存在输出 YES，否则输出NO。
    Sample Input
    3 3 1 6
2 3 4
8 2 6
5 2 9
    Sample Output
    YES

    • 分析：

      • 这算是隐藏比较深的差分约束了，我们可以进行以下推导：

        根据题意有: L<=mp[i][j]*a[i]/b[j]<=R
移项可得:   L/mp[i][j]<=a[i]/b[j]<=R/mp[i][j]
因为我们不用求出具体的值，只需判断是否满足条件，对两边取对数可以把除法变成减法
两边取对数: log(L/mp[i][j])<=log(a[i]/b[j])<=log(R/mp[i][j])
即         log(L/mp[i][j])<=log(a[i])-log(b[j])<=log(R/mp[i][j])
建立不等式  log(b[j])-log(a[i])<=-log(L/mp[i][j]) 
           log(a[i])-log(b[j])<=log(R/mp[i][j])

      • 于是就可以建边了，建边后跑个最短路看看解是否存在即可

      • 由于这样建边没有起点，故我们可以加上一个超级源点，让它与所有点相连，权值为0。

      • 由于这道题时间卡得比较紧，判断是否存在负环时需要优化下，判断条件为入队次数>sqrt(n+m)。

    • code

      //#include <bits/stdc++.h>
#include <cstdio>
#include <cstring>
#include <queue>
#include <cmath>
const int maxn= 400+5;
double dis[maxn];
int vis[maxn],head[maxn];
int n,m,len;
struct node{int to,next;double w;} e[maxn*(maxn+1)];
void Insert(int u,int v,double w){
    e[++len].to=v;e[len].w=w;e[len].next=head[u];head[u]=len;
}
int spfa(int s){
    memset(vis,0,sizeof(vis));memset(dis,0,sizeof(0x4c));
    int cnt[maxn]={0};
    std::queue<int>q;q.push(s);
	vis[s]=1;dis[s]=0;cnt[s]++;    
    while(q.empty()){
        int u=q.front();q.pop();vis[u]=0;
        for(int i=head[u]; i; i=e[i].next){
            int v=e[i].to;double w=e[i].w;
            if(dis[v]>dis[u]+w){
                dis[v]=dis[u]+w;
                if(!vis[v]){
                    vis[v]=1;q.push(v);cnt[v]++;
                    if(cnt[v]>sqrt(n+m))
                        return 0;
                }
            }
        }
    }
    return 1;
}
 
int main(){
    double L,U,x;
    while(~scanf("%d%d%lf%lf",&n,&m,&L,&U))    {
        len=0;memset(head,0,sizeof(head));
        for(int i=1;i<=n;i++)
        	for(int j=1;j<=m;j++){
            	scanf("%lf",&x);//1~n表示行，n+1~n+m表示列
            	Insert(n+j,i,log(U/x));Insert(i,n+j,-log(L/x));
        }
        for(int i=1;i<=n+m;i++)Insert(0,i,0);//0作为超级源点
        if(spfa(0))
            printf("YES\n");
        else printf("NO\n");
    }
    return 0;
}

  3. 查分约束典型例题

    hdu 3592 World Exhibition ★★☆☆☆ 差分约束系统 - 最短路模型 + 判负环
hdu 3440 House Man ★★☆☆☆ 差分约束系统 - 最短路模型 + 判负环
poj 1364 King ★★☆☆☆ 差分约束系统 - 最长路模型 + 判正环
poj 1932 XYZZY ★★☆☆☆ 最长路 + 判正环
hdu 3666 THE MATRIX PROBLEM ★★★☆☆ 差分约束系统 - 最长路模型 + 判正环
poj 2983 Is the Information Reliable? ★★★☆☆ 差分约束系统 - 最长路模型 + 判正环
poj 1752 Advertisement ★★★☆☆ 限制较强的差分约束 - 可以贪心求解
hdu 1529 Cashier Employment ★★★☆☆ 二分枚举 + 差分约束系统 - 最长路模型
hdu 1534 Schedule Problem ★★★☆☆ 差分约束系统 - 最长路模型
ZOJ 2770 Burn the Linked Camp ★★★☆☆
hdu 4109 Instrction Arrangement ★★★☆☆
posted @ 2020-04-27 15:31  ♞老姚♘  阅读(533)  评论(0)  编辑  收藏  举报