拓扑排序

拓扑排序

1. 概念及规则

• 对一个有向无环图(Directed Acyclic Graph简称DAG)G进行拓扑排序，是将G中所有顶点排成一个线性序列，使得图中任意一对顶点u和v，若边<u,v>∈E(G)，则u在线性序列中出现在v之前。通常，这样的线性序列称为满足拓扑次序(Topological Order)的序列，简称拓扑序列。简单的说，由某个集合上的一个偏序得到该集合上的一个全序，这个操作称之为拓扑排序。
• 规则：
  1. 图中每个顶点只出现一次。
  2. A在B前面，则不存在B在A前面的路径。(否则就会形成环)
  3. 顶点的顺序是保证所有指向它的下个节点在被指节点前面！
     • 例如A—>B—>C那么A一定在B前面，B一定在C前面。
     • 这个核心规则下只要满足即可，所以拓扑排序序列不一定唯一！

2. 算法及实现

1. Kahn算法

   • 实现步骤：

     1. 维护一个入度为0的顶点的集合(栈、队列、优先队列皆可)
     2. 每次从该集合中取出一个顶点u(栈顶)
     3. 遍历u的邻接点v,v的入度rd[v]--,如果rd[v]==0,v进栈
     4. 队列为空，出栈数小于n，存在环

   • 时间复杂度：由于每个点入栈出栈一次，每条边扫描一次，时间复杂度为O(n + e)

   • 图示：

     1. 删除1或2以及对应边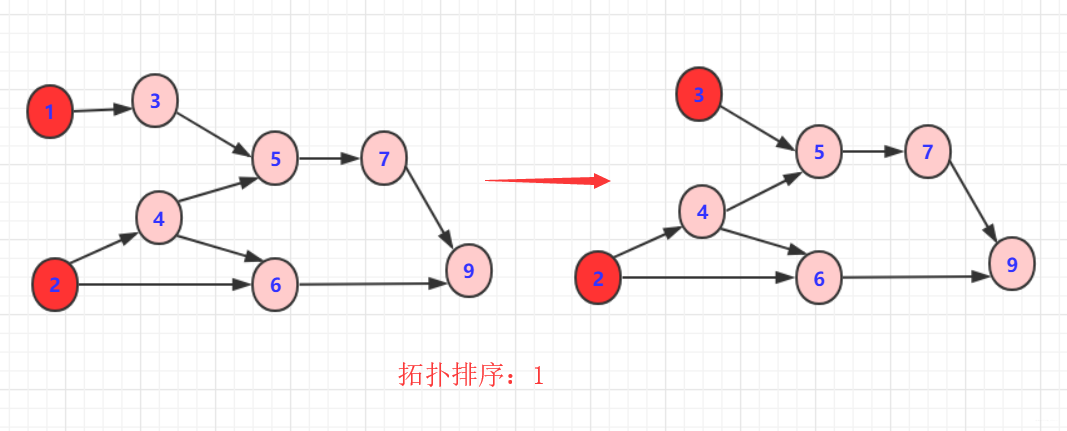

        

     2. 删除2或3以及对应边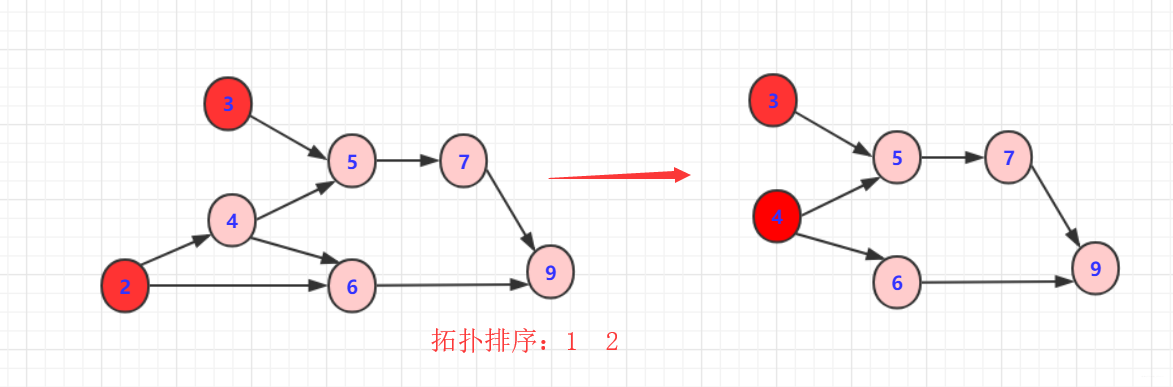

        

     3. 删除3或者4以及对应边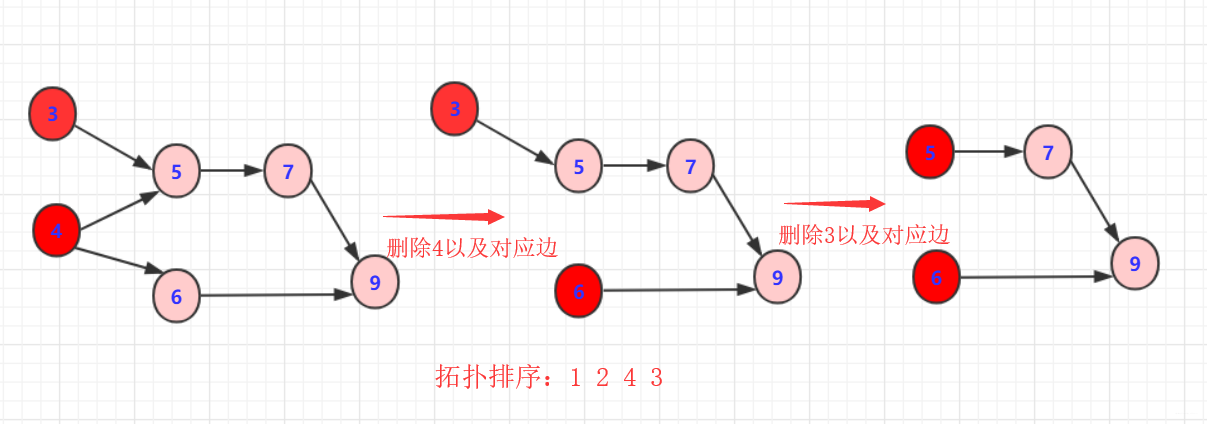

        

     4. 重复以上规则步骤

        

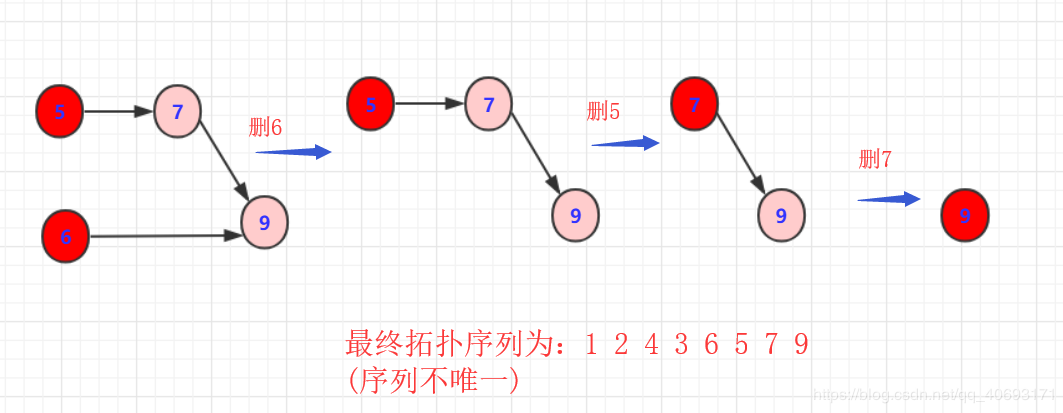
   • 代码：

     #include <bits/stdc++.h>
     const int maxn=100+5,maxm=1e4+5;
     struct Node{int to;int next;}e[maxm];
     int n,m,len,head[maxn],rd[maxn],a[maxn];
     void Insert(int x,int y){
         e[++len].to=y;e[len].next=head[x];head[x]=len;
     }
     void Kahn(){
         std::stack<int> q;
         for(int i=1;i<=n;++i)//入度为0的点进栈
             if(!rd[i])q.push(i);
         int cnt=0;//计算出栈点的个数
         while(!q.empty()){
             int u=q.top();q.pop();a[++cnt]=u;
             for(int i=head[u];i;i=e[i].next){
                 int v=e[i].to;rd[v]--;//相当于删除u的邻接边
                 if(!rd[v])q.push(v);
             }
         }
         if(cnt<n){//说明有环
             printf("Cycle\n");return;
         }
         for(int i=1;i<=cnt;++i)
             printf("%d ",a[i]);
     }
     void Solve(){
         scanf("%d%d",&n,&m);//n个点m条边有向图
         for(int i=1;i<=m;++i){
             int x,y;scanf("%d%d",&x,&y);
             Insert(x,y);rd[y]++;
         }    
         Kahn();
     }
     int main(){
         Solve();
         return 0;
     }
     

2. 基于dfs的算法

   • 以每一个入度为0的点为起点dfs，节点回溯时进栈(类似欧拉回路)，有反向边说明有回路。

   • 图例：

     

     1. 首先2节点的邻接顶点是1和3，由于我们是DFS，它就会一条路走下去，所以先走左边，即到达1号节点
     2. 然后1号节点的邻接顶点是4，所以接下来箭头指向4，4是一个出度为0的节点，它没有邻接顶点，所以不用再往下递归，把4直接保存到栈中。
     3. 接着返回到1节点，此时1节点没有未访问的临界点，把1压入栈中
     4. 然后返回到2节点，接着走右边这条路，到达3号节点，接着从3号节点的邻接顶点出发，但是都已经访问过了，所以返回3后，直接把3压入栈中，最后返回2，把2压入栈中。

   • 代码：

     #include <bits/stdc++.h>
     const int maxn=100+5,maxm=1e4+5;
     struct Node{int to;int next;}e[maxm];
     int n,m,len,cycle,head[maxn],rd[maxn],vis[maxn];
     std::stack<int>q;
     void Insert(int x,int y){
         e[++len].to=y;e[len].next=head[x];head[x]=len;
     }
     void dfs(int u){
     	if(cycle==1)return;//如果已经存在环强制退出
     	vis[u]=-1;//u设为灰点
     	for(int i=head[u];i;i=e[i].next){
     		int v=e[i].to;
     		if(!vis[v])dfs(v);
     		else if(vis[v]==-1){//此时v如果为灰点说明<u,v>是反向边
     			printf("Cycle\n");cycle=1;return;
     		}//return只能退出一个递归
     	}
     	vis[u]=1;q.push(u);//u变黑说明无路可走，进栈
     }
     void Solve(){
         scanf("%d%d",&n,&m);
         for(int i=1;i<=m;++i){
             int x,y;scanf("%d%d",&x,&y);
             Insert(x,y);rd[y]++;
         }    
         for(int i=1;i<=n;++i)//有可能是非连通图
         	if(!rd[i])dfs(i);
         if(cycle==0)//无环则输出拓扑排序
         	while(!q.empty()){
         		printf("%d ",q.top());q.pop();
     		}
     }
     int main(){
         Solve();
         return 0;
     }
     

3. 拓扑排序+dp

Instrction Arrangement(hdu4109)

• 有n个指令m个要求 例如 X,Y,Z 代表 指令Y必须在指令X后Z秒执行 输出cpu运行的最小时间运行最小时间 也就是要满足最大的时间要求。

• 分析：

  • 显然没有任何约束的指令可以在第一秒同时执行。
  • 对有一个或多个约束指令我们要满足最远的那个约束之后
  • 定义dp[i]，表示执行指令i的最早时间，则有：dp[i]=max(dp[i],dp[j]+a[j][i]),a[j][i]表示i必须在j执行后a[j][i]秒后执行。
  • 临界没有任何约束的指令在第一秒时执行，dp[]=1
  • 阶段很明显，当前入度为0点，下个阶段为这些点的临界点。

• 代码

  #include <bits/stdc++.h>
  const int maxn=1000+5,maxm=1e4+5;
  struct Node{int to;int dis;int next;}e[maxm];
  int n,m,len,head[maxn],rd[maxn],dp[maxn];
  void Insert(int x,int y,int z){
      e[++len].to=y;e[len].dis=z;e[len].next=head[x];head[x]=len;
  }
  void Kahn(){
      std::stack<int> q;
      for(int i=0;i<n;++i){//入度为0的点进栈
          if(!rd[i])q.push(i),dp[i]=1;//默认从第一秒开始 
          else dp[i]=0;
      }
      int ans=1; 
      while(!q.empty()){
          int u=q.top();q.pop();
          for(int i=head[u];i;i=e[i].next){
              int v=e[i].to,w=e[i].dis;rd[v]--;//相当于删除u的邻接边
              dp[v]=std::max(dp[v],dp[u]+w);//dp[v]表示运行v最早的时间
  			ans=std::max(ans,dp[v]); 
              if(!rd[v])q.push(v);
          }
      }
      printf("%d\n",ans);
  }
  void Solve(){
  	while(scanf("%d%d",&n,&m)!=EOF){
  		memset(head,0,sizeof(head));
  		memset(rd,0,sizeof(rd));
  		len=0;//边表一定要记得长度清0！！
  		for(int i=1;i<=m;++i){
          	int x,y,z;scanf("%d%d%d",&x,&y,&z);
          	Insert(x,y,z);rd[y]++;
      	}    
      	Kahn();
  	}    
  }
  int main(){
      Solve();
      return 0;
  }
  

4. 总结

• 两种算法时间效率均为O(n+e),边数较多建议用第一种，边数较小可以用dfs，Kahn算法输出序列没有规律，dfs需倒序，输出类似树链,Kahn算法类似广搜。
• Kahn算法适合从前往后推导，dfs算法适合从后往前推导。