十一、图论
11.1 图的基本概念
-
图是一种网状的数据结构,其中的结点之间的关系是任意的,即图中任何两个结点之间都可能直接相关。
-
顶点:图中的数据元素。设它的集合用
V(Vertex)表示。 -
边:顶点之间的关系的集合用
E(edge)来表示: -
顶点的度:连接顶点的边的数量称为该顶点的度。顶点的度在有向图和无向图中具有不同的表示。
- 对于无向图,一个顶点
V的度比较简单,其是连接该顶点的边的数量,记为D(V)。 - 对于有向图要稍复杂些,根据连接顶点
V的边的方向性,一个顶点的度有入度和出度之分。- 入度是以该顶点为端点的入边数量, 记为ID(V)。
- 出度是以该顶点为端点的出边数量, 记为OD(V)。
- 对于无向图,一个顶点
-
无向图(Undigraph):若图中任意\(<v_1,v_2>\in E\)必能推导出\(<v2,v1> \in E\),此时的图称为无向图。
- 无向图用无序对\((v_1,v_2)\),表示\(v_1\)和\(v_2\)之间的一条双向边
(Edge)。 
- 无向图用无序对\((v_1,v_2)\),表示\(v_1\)和\(v_2\)之间的一条双向边
-
有向图(Digraph):如果图中 \(v_1,v_2 \in V\),若存在\(<v_1,v_2> \in E\),而 \(<v_2,v_1>\notin E\) 此时的图称为有向图
- 有向图用有序对\(<v_1,v_2>\),表示\(v_1\)和\(v_2\)之间的一条单向边
(Edge)。 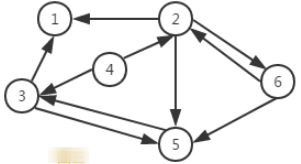
- 有向图用有序对\(<v_1,v_2>\),表示\(v_1\)和\(v_2\)之间的一条单向边
-
无向完全图:如果在一个无向图中, 任意两个顶点之间都存在一条双向边,那么这种图结构称为无向完全图
- 理论上可以证明,对于一个包含
N个顶点的无向完全图,其总边数为N(N-1)/2。 
- 理论上可以证明,对于一个包含
-
有向完全图:如果在一个有向图中,任意两个顶点之间都存在方向相反的两条边,那么这种图结构称为有向完全图。
- 理论上可以证明,对于一个包含
N的顶点的有向完全图,其总的边数为N(N-1)。这是无向完全图的两倍,这个也很好理解,因为每两个顶点之间需要两条边。 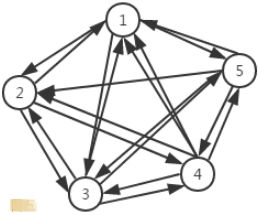
- 理论上可以证明,对于一个包含
-
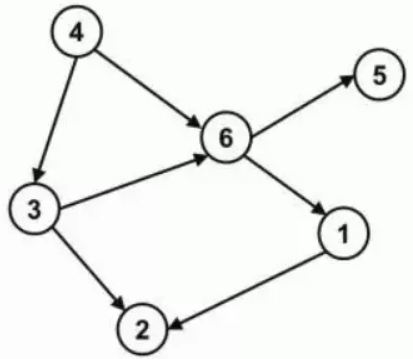
有向无环图(DAG图)
- 如果一个有向图无法从某个顶点出发经过若干条边回到该点,则这个图是一个有向无环图。
- 树型有向图一定是一个有向无环图。
-
自环和平行边:对于节点与节点之间存在两种边,这两种边相对比较特殊
-
自环边
(self-loop):节点自身的边,自己指向自己。 -
平行边(parallel-edges):两个节点之间存在多个边相连接,也叫重边。

-
-
简单图 ( Simple Graph):不存在自环和重边的图叫简单图。
-
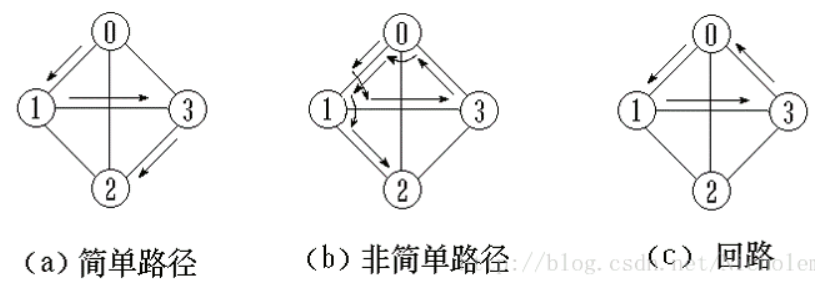
路径、简单路径、回路:
-
路径:无向图中从一个节点到达另一个节点所经过的节点序列
-
简单路径:路径中的各顶点不重复的路径。
-
回路:路径上的第一个顶点和最后一个顶点重合,这样的路径叫做回路。
-
下图箭头表示路径
-
-
连通图与连通分量
-
连通图:无向图
G中,若对任意两点,从顶点 \(V_i\) 到顶点 \(V_j\) 有路径,则称 \(V_i\) 和 $V_j $ 是连通的,图G是一连通图。 -
连通分量:无向图
G的连通子图称为G的连通分量-
任何连通图的连通分量只有一个,即其自身,而非连通的无向图有多个连通分量
-
以下图为例,总共有四个连通分量,分别是:
ABCD、E、FG、HI。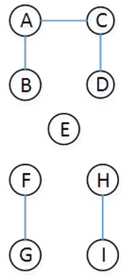
-
-
-
强连通图与强连通分量
-
强连通图:有向图
G中,若对任意两点,从顶点$ V_i$ 到顶点 $V_j $ ,都存在从 $V_i $到 $V_j $ 以及从$ V_j$ 到 \(V_i\) 的路径,则称G是强连通图 -
强连通分量:有向图
G的强连通子图称为G的强连通分量。-
强连通图只有一个强连通分量,即其自身,非强连通的有向图有多个强连通分量。
-
以下图为例,总共有三个强连通分量,分别是:
abe、fg、cdh。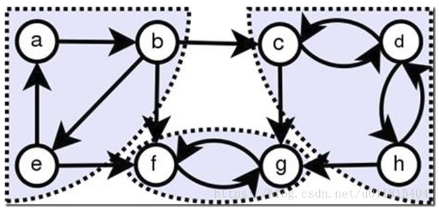
-
-
11.2 图的存储
11.2.1 邻接矩阵
-
设图
G有\(n (n\geq1)\) 个顶点,则邻接矩阵是一个n阶方阵。 -
当矩阵中的
[i,j] !=0(下标从1开始) ,代表其对应的第i个顶点与第j个顶点是连接的。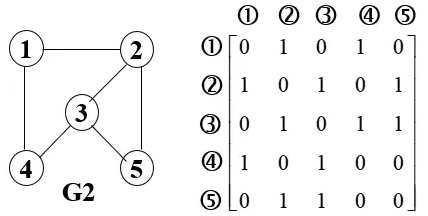
-
邻接矩阵的特点:
- 无向图的邻接矩阵是对称矩阵,
n个顶点的无向图需要n*(n+1)/2个空间大小。 - 有向图的邻接矩阵不一定对称,
n个顶点的有向图需要\(n^2\)的存储空间。 - 无向图中第
i行的非零元素的个数为顶点\(V_i\) 的度。 - 有向图中第
i行的非零元素的个数为顶点 \(V_i\) 的出度,第i列的非零元素的个数为顶点 $V_i $ 的入度 。 - 一般情况下,空间复杂度为 \(O(N^2)\)。
- 无向图的邻接矩阵是对称矩阵,
11.2.2 邻接表(边表)
- 把数组与链表相结合的存储方法称为邻接表。邻接表为图
G中的每一个顶点建立一个单链表,每条链表的结点元素为与该顶点连接的顶点。 - 邻接表的处理办法:
- 顶点用一个一维指针数组存储(较容易读取顶点信息),作为表头,每个数据元素还需要存储指向第一个邻接点的指针,以便于查找该顶点的边信息(更多情况下,表头不需要保存其他信息,因此可以直接定义一个结点类型的指针数组)。
- 每个顶点的所有邻接点构成一个链表。
- 空间复杂度为 \(O(V+E)\),\(V\) 表示结点个数,\(E\) 表示边数。
-
无向图的邻接表结构
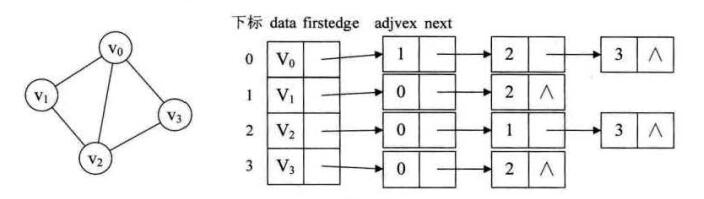
上图中
data是数据域,存储顶点u的信息;firstedge是指针域,指向与结点u相连的第一个结点,即此顶点的第一个邻接点。 边表结点由
adjvex和next两个域组成。adjvex是邻接点域,存储某顶点u的邻接点在顶点v,next则存储指向邻接表中下一个结点的指针,如果不存在下一个结点(即没有边),则指针为NULL。 -
有向图的邻接表和逆邻接表:
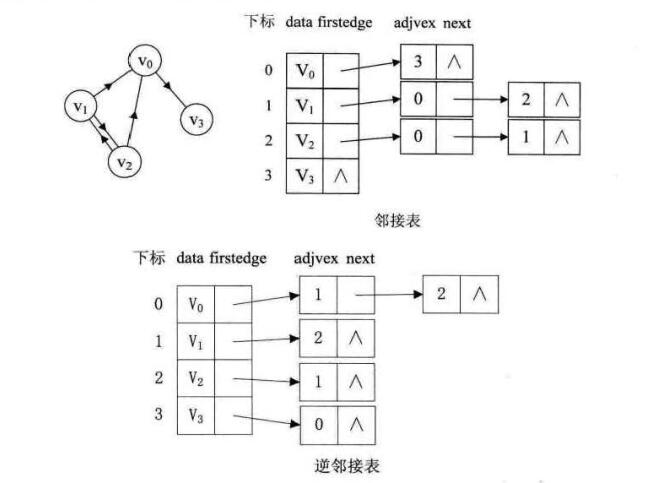
有向图由于有方向,我们是以顶点为弧尾来存储邻接表的,这样很容易就可以得到每个顶点的出度。但也有时为了便于确定顶点的入度或以顶点为弧头的弧,我们可以建立一个有向图的逆邻接表,即对每个顶点
u都建立一个链接为u为弧头的表。 -
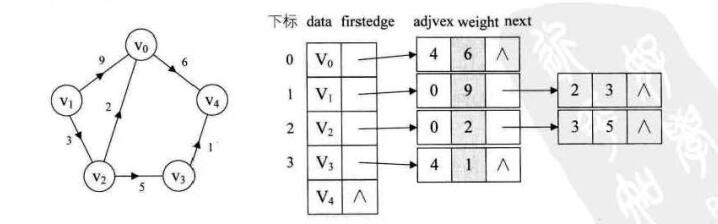
对于带权值的网图,可以在边表结点定义中再增加一个weight的数据域,存储权值信息即可。
-
邻接表创建代码——链表(动态建点):
/* * 向邻接表中添加一条边,从 from 到 to,权值为 w * next 为指向与 from 相邻的下一个结点(另一条边)的指针 */ struct Edge { // 保存链表中的每个结点 int from, to, w; // 通常 from 可以不用,因为表头表示了边的起点编号 Edge* next; }; Edge* head[MAXN]; // 全局变量,定义表头指针数组,大小为结点个数,初始值为 NULL void AddEdge(int from, int to, int w) { Edge* p = new Edge; // 新建一个结点,并将信息进行赋值 p->from = from; p->to = to; p->w = w; p->next = head[from]; // 先将该结点的 next 指向表头指向的结点 head[from] = p; // 更改表头的指向,即可将新结点串进来 } -
邻接表创建代码——前向星(数组实现):
/* * 向邻接表中添加一条边,从 from 到 to,权值为 w * next 为保存与 from 相邻的下一个结点(另一条边)在数组中的位置 */ struct Edge { // 保存链表中的每个结点 int from, to, w; // 通常 from 可以不用,因为表头表示了边的起点编号 int next; }; int head[MAXN]; // 定义表头指针数组,大小为结点个数,初始值为 -1 int tot = 0; // 记录总边数,同时也表示新加的边在数组中的下标 Edge e[MAXM]; // 定义边数组,如果是无向图,大小为给出边数的 2 倍 void AddEdge(int from, int to, int w) { e[tot].from = from; // 将信息赋值到 tot 对应的位置 e[tot].to = to; e[tot].w = w; e[tot].next = head[from]; // 更新新加结点的 next 指向 head[from] = tot; // 更新表头的指向 tot++; // 边数加 1,也作为下一条边的放入的位置 } -
邻接表创建代码——vector 实现:
/* * 向邻接表中添加一条边,从 from 到 to,权值为 w */ struct Edge { // 保存链表中的每个结点 int from, to, w; // 通常 from 可以不用,因为表头表示了边的起点编号 Edge(){} // 不带参的构造函数 Edge(int x, int y, int z) { // 带参构造函数,后面使用方便 from = x; to = y; w = z; } }; vector<Edge> e[MAXN]; // 定义 vector 数组,大小为结点个数,其中的每一个 vector 模拟一个链表 void AddEdge(int from, int to, int w) { e[from].push_back(Edge(from, to, w)); // 将新结点加入到 from 对应的链表 }
注意:如果要保存的图是无向图,则需要双向加边,例如添加一条边 (from, to, w),则需要调用函数 AddEdge(from, to, w); AddEdge(to, from, w); 否则只需要调用一次。
11.2.3 遍历某个结点的邻接点
通常我们需要将与某个结点相邻的所有结点遍历一遍,针对图的不同的存储方式,遍历的方式也不相同。
-
邻接矩阵存储的遍历
// 输出与结点 u 相邻的所有结点,简单明了,不解释 for (int i = 1; i <= n; ++i) { if (g[u][i] != -1) { // 假设我们用 -1 表示 u 与 i 之间没有边 printf("%d ", i); } } -
邻接表存储的遍历
这种存图的方式是我们常用的,所以一定要熟练掌握。根据上面给出的不同的构建方法,给出示例代码来输出 结点 u 的所有邻接点编号。
-
链表(指针实现):
// 从表头开始,访问完一个邻接点后,通过 next 调到下一个邻接点 for (Edge* p = head[u]; p != NULL; p = p->next) { printf("%d ", p->to); } -
前向星(数组实现):
// 从表头开始,访问完一个邻接点后,通过 next 调到下一个邻接点 for (int i = head[u]; i != -1; i = e[i].next) { printf("%d ", e[i].to); } -
vector 实现:
// 从表头开始,访问完一个邻接点后,通过 next 调到下一个邻接点 int gs = e[u].size(); for (int i = 0; i < gs; ++i) { printf("%d ", e[i].to); }
-
11.3 图的遍历
- 从图中某一顶点出发访遍图中其余顶点,且使每一个顶点仅被访问一次,这一过程就叫做图的遍历。
- 根据遍历路径的不同,通常有两种遍历图的方法:深度优先遍历和广度优先遍历。
11.3.1 深度优先遍历
-
深度优先遍历
(Depth_First_Search)也称为深度优先搜索,简称为DFS。 -
它是从图中某个顶点
v出发,访问此顶点,然后从v的未被访问的邻接点出发深度优先遍历图,直至图中所有和v有路径相通的顶点都被访问到。 -
对于非连通图,只需要对它的连通分量分别进行深度优先遍历即可。接下来我们以一个示例演示图的深度优先遍历。如下图所示:

- 在开始进行遍历之前,我们还要准备一个数组,用来记录已经访问过的元素。其中
0代表未访问,1代表已访问,如下所示:

-
假设我们是在走迷宫,
A是入口,每次都向右手边前进。首先从A走到B,结果如下: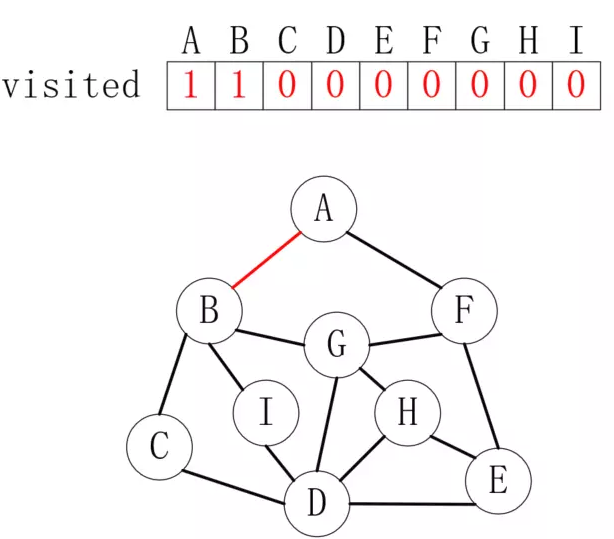
-
B之后有三个路,我们依然选择最右边,如此下去,直到走到F,如下所示:
-
到达
F后,如果我们继续按照向右走的原则,就会再次访问A,但A已访问,则访问另一个邻接点G,如下所示: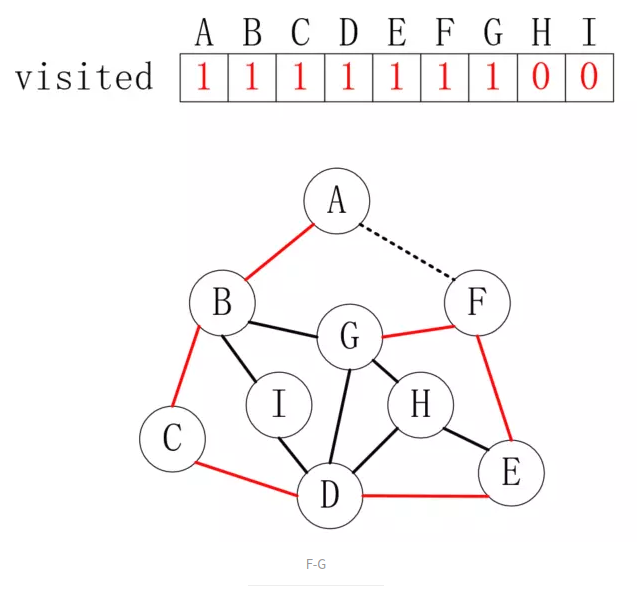
-
到达
G后,可以发现B和D都走过了,这时候走到H,如下所示: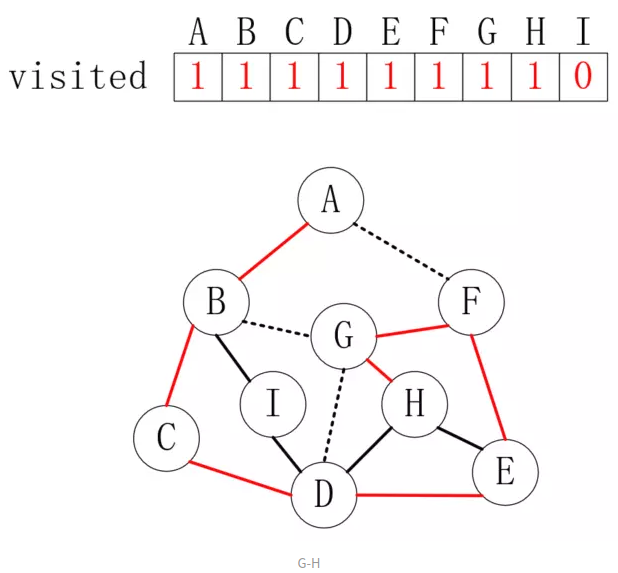
-
到达
H后,H的邻接点都已访问过了,所以我们从H退回到上层节点G,发现G,F,E的邻接点全部已经访问过了,直到退回到D时,发现I还没走过,于是访问顶点I,如下所示: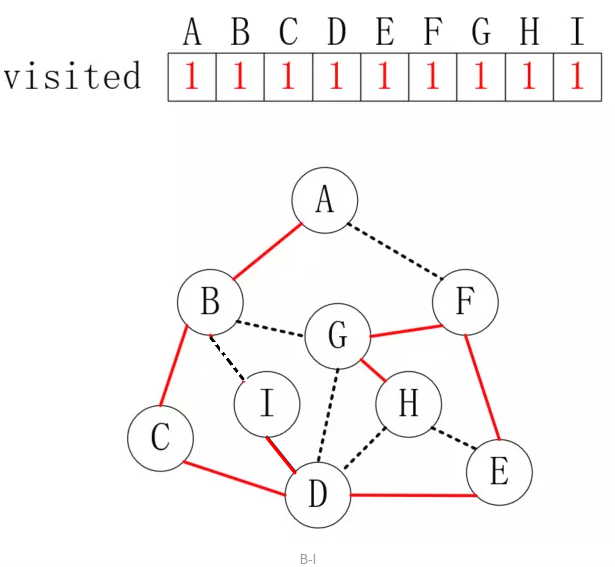
-
同理,访问
I之后,发现与I连通的顶点都访问过了,所以再向前回退,直到回到顶点A,发现全部顶点都访问过了,至此遍历完毕。
- 在开始进行遍历之前,我们还要准备一个数组,用来记录已经访问过的元素。其中
-
下面给出的深度优先遍历的参考程序,假设图以邻接表存储(其他情况自己处理即可)
void dfs(int i) { //邻接表存储图,访问点 i visited[i] = true; //标记为已经访问过 for (Edge* p = head[i]; p != NULL; p = p->next) { // 深度优先遍历 i 的所有邻接点 if (!visited[p->to]) { dfs(p->to); } } } // 假设全局变量已经定义好了 int main() { memset(visited, false, sizeof(visited)); // 如果是有向图,必须用循环才能保证所有的结点都遍历到 // 如果是连通的无向图,从任一结点开始即可 for (int i = 1; i <= n; ++i) { if (!visited[i]) { dfs(i); } } return 0; }
11.3.2 广度优先搜索
广度优先遍历并不常用,从编程复杂度的角度考虑,通常采用的是深度优先遍历。
深度优先遍历可以认为是纵向遍历图,而广度优先遍历(Breadth_First_Search)则是横向进行遍历。还以上图为例,不过为了方便查看,我们把上图调整为如下样式:
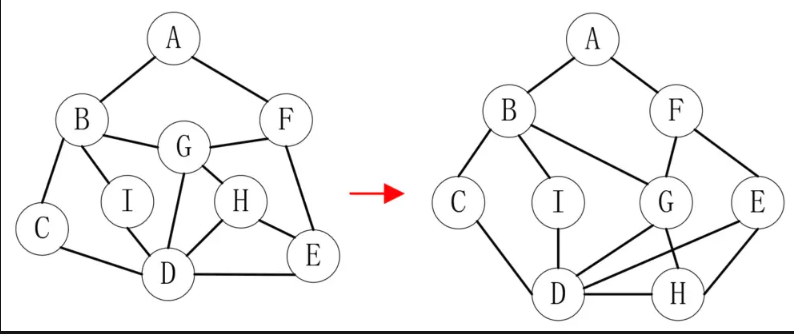
我们依然以 A 为起点,把和 A 邻接的 B 和 F 放在第二层,把和 B、F 邻接的 C、I、G、E 放在第三层,剩下的放在第四层。
广度优先遍历就是从上到下一层一层进行遍历,这和树的层序遍历很像。我们依然借助一个队列来完成遍历过程,因为和树的层序遍历很像,这里只展示结果,如下所示:
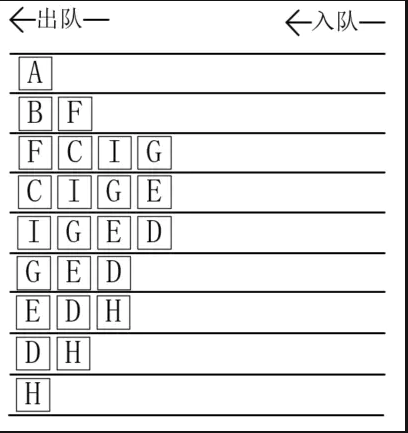
广度优先遍历和广搜 BFS 相似,因此使用广度优先遍历一张图并不需要掌握什么新的知识,在原有的广度优先搜索的基础上,做一点小小的修改,就成了广度优先遍历算法。
void bfs(int s) { //邻接表存储图,访问点 s
queue<int> que;
visited[s] = true; // 将起点 s 标记并放到队列
que.push(s);
while (!que.empty()) { //
int now = que.front();
printf("%d ", now);
for (Edge* p = head[now]; p != NULL; p = p->next) { // 广度优先遍历邻接点
if (!visited[p->to]) {
que.push(p->to); // 找到未被访问过的邻接点加入队列,并标记
visited[p->to] = true;
}
}
}
}
// 假设全局变量已经定义好了
int main() {
memset(visited, false, sizeof(visited));
// 如果是有向图,必须用循环才能保证所有的结点都遍历到
// 如果是连通的无向图,从任一结点开始即可
for (int i = 1; i <= n; ++i) {
if (!visited[i]) {
bfs(i);
}
}
return 0;
}
11.4 欧拉路
11.4.1 基本概念
- 如果一个图存在一笔画,则一笔画的路径叫做欧拉路,如果最后又回到起点,那这个路径叫做欧拉回路。
- 欧拉图:存在欧拉回路的图称作欧拉图。
- 半欧拉图:存在欧拉路径但不存在欧拉回路的图称作半欧拉图。
- 欧拉图、半欧拉图的判定
- 无向图
- 奇点:跟这个点相连的边数目有奇数个的点。对于能够一笔画的图,我们有以下两个定理。
- 定理1:无向图
G为欧拉图,当且仅当G为连通图,且所有顶点度为偶数,即奇点为零。 - 定理2:无向图
G为半欧拉图,当且仅当G为连通图,且除了两个顶点的度为奇数外,其它顶点度为偶数,即存在两个奇点。 - 半欧拉图的欧拉路径起点必须是一个奇点,终点是另一个奇点,欧拉图任一点均可成为起点。
- 两个定理的正确性是显而易见的,既然每条边都要经过一次,那么对于欧拉路,除了起点和终点外,每个点如果进入了一次,显然一定要出去一次,显然是偶点。
- 对于欧拉回路,每个点进入和出去次数一定都是相等的,显然没有奇点。
- 有向图
- 基图:忽略有向图所有边的方向,得到的无向图称为该有向图的基图。
- 定理1:有向图
G为欧拉图,当且仅当G的基图连通,且所有顶点的入度等于出度。 - 定理2:有向图
G为半欧拉图,当且仅当G的基图连通,且存在顶点u的入度比出度大1,v的入度比出度小1,其它所有顶点的入度等于出度。
- 无向图
11.4.2 Hierholzer 算法
-
一个无向图如果存在欧拉路经,那么我们如何遍历才能找到一条欧拉路经呢?
-
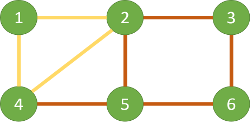
假设上图我们其中一种走法是:我们从点
4开始,一笔划到达了点5,形成路径4-5-2-3-6-5。此时我们把这条路径去掉,则剩下三条边,2-4-1-2可以一笔画出。显然上面走法不是欧拉路 -
我们用
+代表入栈,-代表出栈,把刚才的路经重新描述一下:4+ 5+ 2+ 3+ 6+ 5+ 5- 6- 3- 1+ 4+ 2+ 2- 4- 1- 2- 5- 4-- 把所有出栈的记录连接起来,得到
5-6-3-2-4-1-2-5-4 - 我们把上面的出栈序列倒序输出,正好是一个从
4开始到5结束的一条欧拉回路。
-
算法实现:
#include <cstdio> #include <cstring> const int maxn = 500 + 5,maxe=2*1024+5;//无向图一定注意边数要翻倍 struct Node{//节点定义 int to,next; }a[maxe];//存储边 int Head[maxn],len=0;//len记录边数,Head[u]表示以u为起点的边在边表中的编号。 int Path[maxe],cnt=0;//记录回路的节点,每条边要访问一次所以点数=边数+1 bool vis[maxe];//记录边是否已访问 void Insert(int x,int y){//边表的建立x起点,y为终点 a[len].to=y;a[len].next=Head[x];Head[x]=len++; }//要用位运算标记无向图的正反两条边,所以边的编号从0开始。 void Dfs(int u){//递归的最大深度为边数,当边数较大时容易爆栈,可以改为非递归 for(int i=Head[u];i!=-1;i=a[i].next){ if(vis[i])continue;//第i条边已访问 vis[i]=vis[i^1]=1;//i是i^1的反向边,把这两条边设为已访问 Head[u]=i;//优化,前面的边已经走过了,没有必要每次从最后一个位置往前找了 int v=a[i].to;Dfs(v);//从第i条边的终点深搜 i=Head[u];//优化,有可能v的子树中也更新过了u的共点边 } Path[++cnt]=u;//u回溯时记录路径经过点u } void Euler(int u){////递归的最大深度为边数,当边数较大时容易爆栈,可以改为非递归 std::stack<int> q; q.push(u);//把起点u进栈 while(!q.empty()){ int i,x=q.top(); for(i=Head[x];i!=-1 && vis[i];i=a[i].next); //跳出循环时i==-1或第i条边已访问即vis[i]=1 if(i==-1){//说明x已不存在未访问的邻接边 Path[++cnt]=x;q.pop(); } else{//说明第i条未访问 q.push(a[i].to);//第i条边的去边进栈 vis[i]=vis[i^1]=1;//标记第i条边及其反向边 Head[x]=a[i].next;//指向下一条未访问过的邻接边 } } } void Solve(){ int m;scanf("%d",&m); memset(Head,-1,sizeof(Head));//边的编号从0开始,所以要初始化为-1 for(int i=1;i<=m;++i){ int x,y;scanf("%d%d",&x,&y); Insert(x,y);Insert(y,x);//无向图要加双向,有向图只加一遍 } Dfs(1);//欧拉图随便一个点都可以作为源点 for(int i=cnt;i>0;--i)//逆序输出路径 printf("%d\n",Path[i]); } int main(){ Solve(); return 0; }
11.5 最短路
- 最短路径问题是图的又一个比较典型的应用问题。例如,某一地区的一个公路网,给定了该网内的
n个城市以及这些城市之间的相通公路的距离,能否找到城市A到城市B之间一条距离最近的通路呢? - 如果将城市用点表示,城市间的公路用边表示,公路的长度作为边的权值,那么,这个问题就可归结为在网中,求点
A到点B的所有路径中边的权值之和最短的那一条路径。 - 这条路径就是两点之间的最短路径,并称路径上的第一个顶点为源点(
Sourse),最后一个顶点为终点(Destination)。 
11.5.1 迪杰斯特拉(Dijkstra)
- 迪杰斯特拉(Dijkstra)算法是典型最短路径算法,用于计算一个节点到其他节点的最短路径。
- 它的主要特点是以起始点为中心向外层层扩展(广度优先搜索思想),直到扩展到终点为止。
11.5.1.1 算法思路
-
通过
Dijkstra计算图G中的最短路径时,需要指定起点s(即从顶点s开始计算)。 -
引入两个集合
(S , U),S集合包含已求出的最短路径的点(以及相应的最短长度),U集合包含未求出最短路径的点。 -
操作步骤:
- 初始时,
S只包含起点s;U包含除s外的其他顶点,且U中顶点的距离为:起点s到该顶点的距离(s的邻接点的距离为边权,其他点为∞) - 从
U中选出距离源点s最短的顶点k,并将顶点k加入到S中;同时,从U中移除顶点k。 - 松弛操作:利用
k更新U中各个顶点到起点s的距离。 - 重复步骤
2)和3),直到遍历完所有顶点。
- 初始时,
-
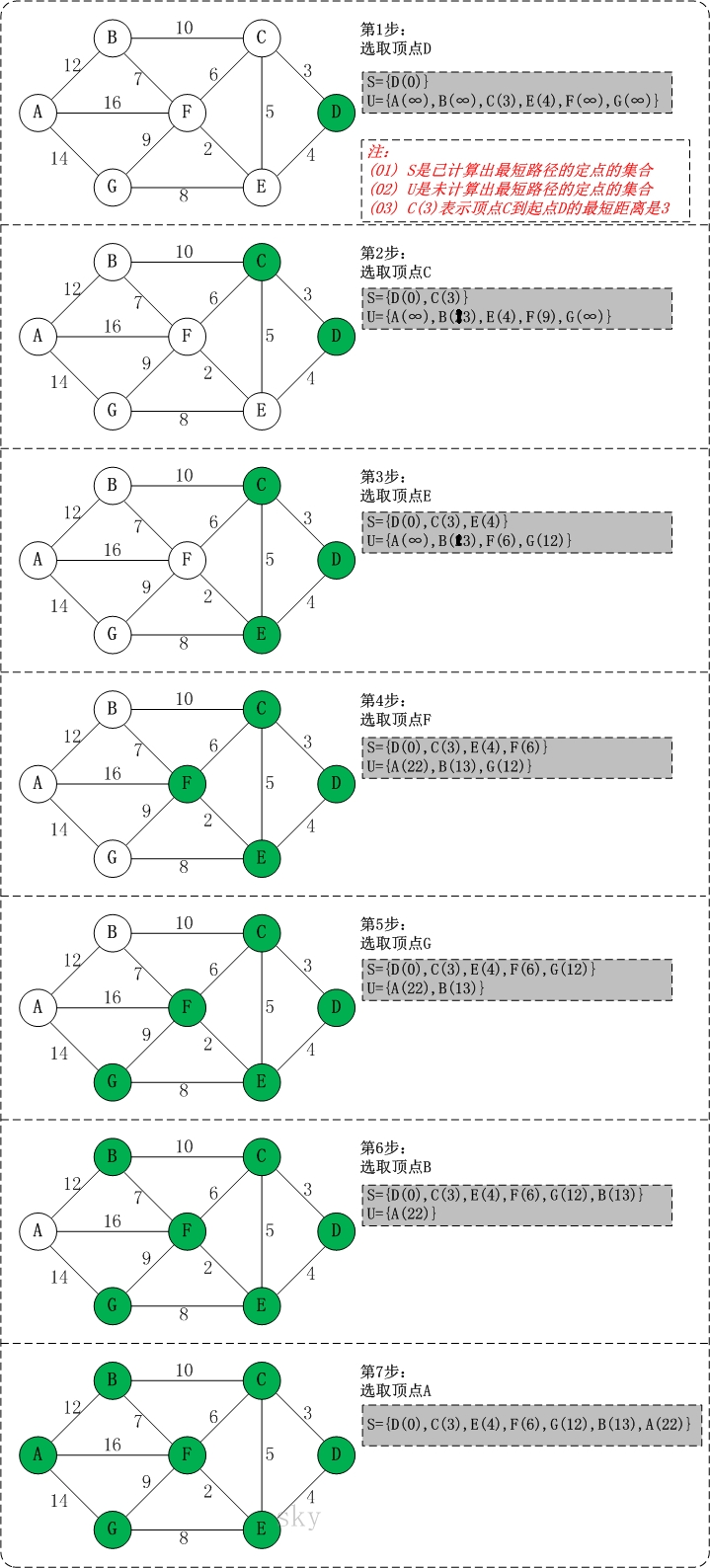
图解
-
代码实现
#include <cstdio> #include <cstring> const int maxn = 100 + 5,Inf=0x3f3f3f3f;//两个Inf相加不会超int int n,a[maxn][maxn],dis[maxn],path[maxn];//dis[i]表示i到源点的最短距离,path[i]记录路径 void Dijs(int s){//源点s bool f[maxn];memset(f,0,sizeof(f));//f[i]表示i到源点s的最短距离已求出 f[s]=1;//源点进确定集合 for(int i=1;i<=n;++i){//除邻接点外,其他点离源点距离初始化为Inf if(a[s][i]){ dis[i]=a[s][i];path[i]=s; } else dis[i]=Inf; } dis[s]=0;path[s]=s;//源点s到自己的距离为0 for(int i=1;i<n;++i){//每次能确定一个点到源点的最短路,n-1次能求出所有 int Min=Inf,k=0;//每次从不在确定集合的点中找出离源点最近的点 for(int j=1;j<=n;++j){ if(!f[j] && Min>dis[j]){ Min=dis[j];k=j;//k记录最近的点 } } f[k]=1;//k到源点距离已确定,进集合 for(int j=1;j<=n;++j)//经过k进行松弛操作 if(a[k][j] && dis[j]>dis[k]+a[k][j]){ dis[j]=dis[k]+a[k][j];path[j]=k; } } } void Solve(){ int m;scanf("%d%d",&n,&m);//n个顶点,m条边 for(int i=1;i<=m;++i){ int x,y,z;scanf("%d%d%d",&x,&y,&z); a[x][y]=a[y][x]=z;//x到y的距离为z } Dijs(4);//节点4为源点 for(int i=1;i<=n;++i)//输出每个点到源点的最短距离 printf("%d ",dis[i]); } int main(){ Solve(); eturn 0; } /*数据为上图样例 7 12 1 2 12 1 6 16 1 7 14 2 3 10 2 6 7 3 4 3 3 5 5 3 6 6 4 5 4 5 6 2 5 7 8 6 7 9 */- 时间效率 \(O(n^2)\) ,
n-1次的松弛必不可少,但需要O(n)的时间效率去找最小的边,再用O(n)的效率去松弛,对这一部分我们可以用堆进行优化。
- 时间效率 \(O(n^2)\) ,
11.5.1.2 堆优化的 Dijkstra
-
对于上一节普通的最短路算法我们可以进行如下优化:
- 对于松弛部分,我们可以用邻接表的存储方式进行优化,对一个节点较多的图来说一般来说邻接表的遍历方式是常数的,远远小于
O(n)。 - 对求集合外的节点到源点的最小值,我们可以建一个小根堆,这样我们时间消耗就是进堆的操作,为
O(ElogE),我们可以用有限队列进行操作。
- 对于松弛部分,我们可以用邻接表的存储方式进行优化,对一个节点较多的图来说一般来说邻接表的遍历方式是常数的,远远小于
-
代码实现
#include <bits/stdc++.h> const int maxn=1000+5,maxe=1e4*2+5; struct Node{ int num,dis; Node(){}; Node(int x,int y){num=x;dis=y;} bool operator <(const Node &a)const{//优先队列默认大根堆所以重载 return dis > a.dis;//小根堆 } }; struct Edge{//边节点 int to,dis,next; }a[maxe]; int dis[maxn],Head[maxn],len;//dis[i]表示i到源点的最短距离,Head,len同边表 void Insert(int x,int y,int z){//边表创建,此处最小边编号为1 a[++len].to=y;a[len].dis=z;a[len].next=Head[x];Head[x]=len; } void Dijs(int x){ std::priority_queue <Node> q;//优先队列,以距离为key的小根堆 bool f[maxn];memset(f,0,sizeof(f));//f[i]标记是否在确认集合 memset(dis,0x3f,sizeof(dis));//初始化其他节点到源点的最小距离为无穷大 dis[x]=0;//源点到自己的距离为0 q.push(Node(x,0));//源点进队 while(!q.empty()){//队列非空说明还有点可以松弛 Node t=q.top();q.pop();//取出堆顶的点并出堆,必然到源点的距离最小 int k=t.num; if(f[k])continue;//如果k到源点的最短路已经求出,说明其邻接点已经松弛 f[k]=1;//k点进确定集合 for(int i=Head[k];i;i=a[i].next){//以k为中间点松弛k的邻接点 int y=a[i].to,d; if(dis[y]>(d=dis[k]+a[i].dis)){ dis[y]=d;q.push(Node(y,d));//松弛成功k的邻接点y进堆 } } } } void Solve(){ int m,n;scanf("%d%d",&n,&m); for(int i=1;i<=m;++i){ int x,y,z;scanf("%d%d%d",&x,&y,&z); Insert(x,y,z);Insert(y,x,z);//无向图 } Dijs(4); for(int i=1;i<=n;++i) printf("%d ",dis[i]); } int main(){ Solve(); return 0; } -
迪杰斯拉算法的核心思想是贪心,此贪心思想是建立在权值为正的基础上,所以此算法无法解决权值为负的问题。
11.5.2 Bellman-Ford 算法
-
算法的基本思路:以任意顺序考虑图的边,沿着各条边进行松弛操作,重复操作
V次(V表示图中顶点的个数)。 -
对有向带权图
G = (V, E),从顶点s起始,利用Bellman-Ford算法求解各顶点最短距离,算法描述如下:for(i = 0;i < V;i++) for each edge(u,v) ∈ E //对每一条边 Relax(u,v);//松弛操作- 算法对每条边做松弛操作,并且重复
V次,所以算法可以在于O(V*E)成正比的时间内解决单源最短路径问题。
- 算法对每条边做松弛操作,并且重复
-
代码实现:
#include <bits/stdc++.h> const int maxn = 10000 + 5,maxe=1e5 + 5; struct Node{ int from,to,dis;//不需要边表,注意跟边表的区别 }a[2*maxe];//无向图 int d[maxn];//d[i]表示i到源点的最短距离 int m,n,len=0; void Insert(int x,int y,int z){//建边 a[++len].from=x;a[len].to=y;a[len].dis=z; } bool Check(){//对所有边再做一次松弛,如果成功返回1 for(int i=1;i<=len;++i){//遍历每条边 int x=a[i].from,y=a[i].to,z=a[i].dis; if(d[y]>d[x]+z)return 1;//松弛成功 } return 0; } void Bellman_ford(int u){ memset(d,0x3f,sizeof(d));//初始化其他点到源点的最短距离为无穷大 d[u]=0;//源点到自己的最短距离为0 for(int i=1;i<n;++i){//对每条边做n-1次松弛 for(int j=1;j<=len;++j){//遍历每条边 int x=a[j].from,y=a[j].to,z=a[j].dis; d[y]=std::min(d[y],d[x]+z);//松弛操作 } } } void Solve(){ scanf("%d%d",&n,&m); for(int i=1;i<=m;++i){ int x,y,z;scanf("%d%d%d",&x,&y,&z); Insert(x,y,z);Insert(y,x,z); } Bellman_ford(4); if(Check()){//松弛完n-1次后如果还能松弛成功说明有负环回路 printf("NO\n");return; }//无法松弛说明不存在负权回路 for(int i=1;i<=n;++i) printf("%d ",d[i]); } int main(){ Solve(); return 0; } -
Dijkstra算法和Bellman-ford算法的区别:Dijkstra算法在求解的过程中,源点到集合S内各顶点的最短路径一旦求出,则之后就不变了,修改的仅仅是源点到未确定最短距离的集合T中各顶点的最短路路径长度。Bellman-ford算法在求解过程中,源点到各顶点的最短距离知道算法结束才能确定下来。Bellman-ford能解决负权问题,也可以判断图中是否存在负环,而Dijkstra只能解决权值为正的问题。
11.5.3 spfa算法
-
spfa可以看成是Bellman-ford的队列优化版本。 -
Bellman每一轮用所有边来进行松弛操作可以多确定一个点的最短路径,但是用每次都把所有边拿来松弛太浪费了。 -
只有那些松弛成功的点才有可能松弛它的邻接点,所以我们可以用一个队列记录松弛成功点的,依次用这些点去松弛邻接点。
-
代码实现:
#include <bits/stdc++.h>
const int maxn = 10000 + 5,maxe=1e5 + 5;
struct Node{
int to,dis,next;
}a[maxe];
int d[maxn],head[maxn];//d[i]表示i到源点的最短距离
int m,n,len=0,cnt[maxn];//cnt[i]记录节点i进队次数
bool inq[maxn];//inq[i]=0表示节点i在队列
void Insert(int x,int y,int z){
a[++len].to=y;a[len].dis=z;a[len].next=head[x];head[x]=len;
}
bool spfa(int s){//返回0表示不存在最短路,即有负环
memset(d,0x3f,sizeof(d));d[s]=0;//除了源点,其他点到源点最短距离为无穷
std::queue<int>q;q.push(s);inq[s]=1;//源点入队
while(!q.empty()){
int u=q.front();q.pop();//取出队首,并出队
inq[u]=0;//顶点可以反复入队,所以出队后要把标记设为0
for(int i=head[u];i;i=a[i].next){
int v=a[i].to,dis;
if(d[v]>(dis=d[u]+a[i].dis)){//松弛成功
d[v]=dis;
if(!inq[v]){//节点v不在队列中
if(++cnt[v]>=n)return 0;//一个点被松弛n次,肯定有负环
q.push(v);inq[v]=1;
}
}
}
}
return 1;
}
void Solve(){
scanf("%d%d",&n,&m);
for(int i=1;i<=m;++i){
int x,y,z;scanf("%d%d%d",&x,&y,&z);
Insert(x,y,z);Insert(y,x,z);
}
if(!spfa(4)){
printf("NO\n");return;
}
for(int i=1;i<=n;++i)
printf("%d ",d[i]);
}
int main(){
Solve();
return 0;
}
spfa算法对随机数据效果很好,甚至比堆优化的dijkstra还要快。但如果在处理非负权的最短路时不建议使用spfa容易被卡。spfa有一般有三种简单的优化,这三种优化都是把队列换成双端队列,但都容易被正对性数据卡掉,LLL优化:每次将入队结点距离和队内距离平均值比较,如果更大则插入至队尾,否则插入队首。Hack:向1连接一条权值巨大的边,这样LLL就失效了。
SLF优化:每次将入队结点距离和队首比较,如果更大则插入至队尾,否则插入队首。- Hack:使用链套菊花的方法,在链上用几个并列在一起的小边权边就能欺骗算法多次进入菊花。
SLF带容错:每次将入队结点距离和队首比较,如果比队首大超过一定值则插入至队尾,否则插入队首。- 卡法是卡 SLF 的做法,并开大边权,权值总和最好超过 \(10^{12}\)。
11.5.4 Floyd 算法
-
Floyd算法 (Floyd-Warshall algorithm) 又称为弗洛伊德算法、插点法,是解决给定的加权图中顶点间的最短路径的一种算法。 -
该算法名称以创始人之一、1978年图灵奖获得者、斯坦福大学计算机科学系教授罗伯特·弗洛伊德命名。
-
适用范围:无负权回路即可,边权可正可负,运行一次算法即可求得任意两点间最短路。
-
问题模型:
-
某个国家有
n个城市,这n个城市间有m条公路相连 ,第i条公路长度为 \(a_i\) 。我们现在需要求任意两个城市之间的最短路程,也就是求任意两个点之间的最短路径。这个问题这也被称为“多源最短路径”问题。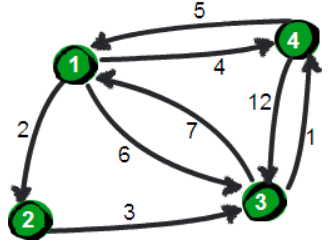
-
上图中有
4个城市8条公路,公路上的数字表示这条公路的长短。请注意这些公路是单向的。 -
Floyd算法的数据的存储,我们一般用邻接矩阵,即一个二维数组来存储。

-
算法分析:
-
如果要让任意两点 (例如从顶点
A点到顶点B) 之间的路程变短,只能引入第三个点 (顶点K) ,并通过这个顶点K中转即A-> K -> B,才可能缩短其距离。 -
假如现在只允许经过
1号顶点,即K=1来中转,求任意两点之间的最短路程,我们只需判断节点1是否能松弛当前边即可。//核心代码 for(int i=1;i<=n;++i)//枚举边的起点 for(int j=1;j<=n;++j)//枚举边的终点 if(a[i][j]>a[i][1]+a[1][j])//如果1能松弛边i->j a[i][j]=a[i][1]+a[1][j]; -
通过节点
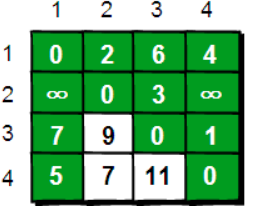
1松弛后结果如下图所示。 -
-
接下来继续求在只允许经过
1和2号两个顶点的情况下任意两点之间的最短路程。//经过1号顶点 for(int i=1;i<=n;++i)//枚举边的起点 for(int j=1;j<=n;++j)//枚举边的终点 if(a[i][j]>a[i][1]+a[1][j])//如果1能松弛边i->j a[i][j]=a[i][1]+a[1][j]; //经过2号顶点 for(int i=1;i<=n;++i)//枚举边的起点 for(int j=1;j<=n;++j)//枚举边的终点 if(a[i][j]>a[i][2]+a[2][j])//如果2能松弛边i->j a[i][j]=a[i][2]+a[2][j];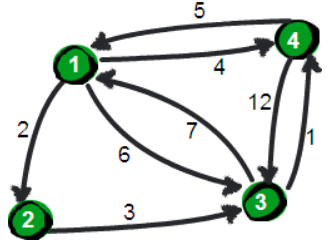
-
依此类推,我们只要依次枚举中转点即可。
for(int k=1;k<=n;++k)//枚举中转点 for(int i=1;i<=n;++i)//枚举边的起点 for(int j=1;j<=n;++j)//枚举边的终点 if(a[i][j]>a[i][k]+a[k][j])//松弛操作 a[i][j]=a[i][k]+a[k][j];
-
-
时间效率:\(O(n^3)\)
-




