十、树
10.1 树的基本概念
-
树(
tree),是一种抽象数据类型或是实现这种抽象数据类型的数据结构,用来模拟具有树状结构性质的数据集合。 -
树是一种非线性的数据结构,用它能很好地描述有分支和层次特性的数据集合。
-
树是由
n(n>0)个元素组成的有限集合,其中:-
每个元素称为结点(node);
-
有一个特定的结点,称为根结点或树根
(root); -
除根结点外,其余结点能分成
m(m>=0)个互不相交的有限集合\(T_0,T_1,T_2,……T_{m-1}\)。其中的每个子集又都是一棵树,这些集合称为这棵树的子树。 -
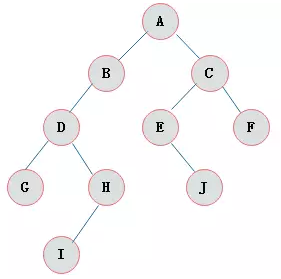
如下图是一棵典型的树:
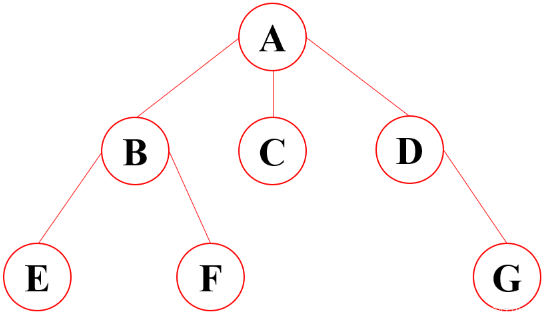
-
-
树的结点
- 结点的度:结点拥有的子树的数目。eg:结点
A的度为2 - 树的度:树种各结点度的最大值。eg:树的度为
3 - 叶子结点:度为 0 的结点。eg:
G,H,I,J,F为叶子结点 - 分支结点:度不为0的结点称为分支结点;
- 内部结点:根以外的分支结点又称为内部结点;
- 在用图形表示的树型结构中:
- 树枝:连接相关联的两个结点的线段
- 父结点:树枝的上端结点为下端结点的父结点
- 子结点:树枝的下端结点为上端结点的子结点。
- 兄弟结点:称同一个父结点的多个子结点为兄弟结点。
- 祖先结点:从根结点到某个子结点所经过的所有结点为这个子结点的祖先。如:结点
A,B,D为是结点G的祖先。
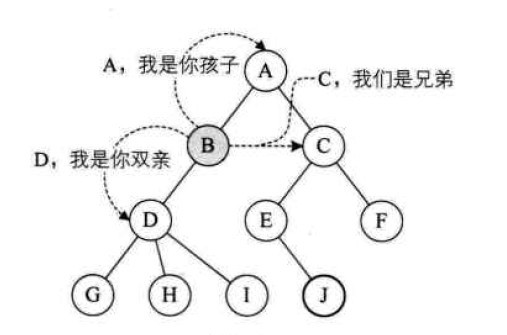
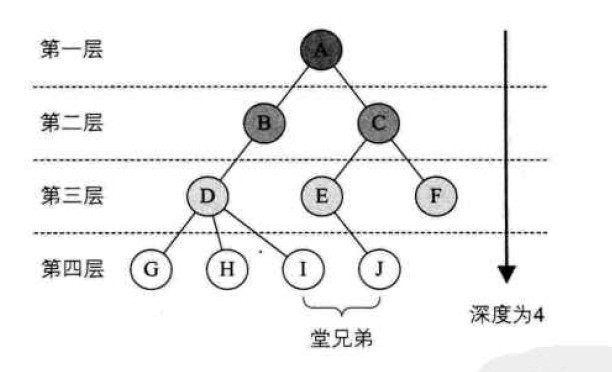
- 结点的层次:根结点为第一层,根的子结点为第二层,依次向下递推…
- 树的深度:树种结点的最大层次。eg:该树的深度为
4 - 森林:互不相交的树称为森林
- 结点的度:结点拥有的子树的数目。eg:结点
10.2 指针
10.2.1 指针的概念
- 指针是一种保存变量地址的变量。
- C++语言里,变量存放在内存中,而内存其实就是一组有序字节组成的数组,每个字节有唯一的内存地址。
- CPU 通过内存寻址对存储在内存中的某个指定数据对象的地址进行定位。
- 数据对象是指存储在内存中的一个指定数据类型的数值或字符串,它们都有一个自己的地址,而指针便是保存这个地址的变量。
- 内存其实就是一组有序字节组成的数组,数组中,每个字节大大小固定,都是
8bit。对这些连续的字节从0开始进行编号,每个字节都有唯一的一个编号,这个编号就是内存地址。示意如下图: 
- 上图左侧的连续的十六进制编号就是内存地址,每个内存地址对应一个字节的内存空间。而指针变量保存的就是这个编号,也即内存地址。
10.2.2 指针变量的定义
-
类型 * 变量名;
int *p; // 声明一个 int 类型的指针 p char *p; // 声明一个 char 类型的指针 p int *arr[10]; // 声明一个指针数组,该数组有10个元素,其中每个元素都是一个指向 int 类型对象的指针 int (*arr)[10]; // 声明一个数组指针,该指针指向一个 int 类型的一维数组 int **p; // 声明一个指针 p ,该指针指向一个 int 类型的指针- ***** 号标识该变量为指针类型,当定义多个指针变量时,在每个指针变量名前面均需要加一个 *,不能省略,否则为非指针变量。
- ***** 指针运算符的优先级别低于数组下标
[],所以int *a[10];表示定义了10个int型指针变量,int (*a)[10];表示定义了一个指向有十个元素的整型数组。
10.2.3 指针的初始化
-
声明一个指针变量并不会自动分配任何内存。
-
对指针进行间接访问之前,指针必须进行初始化:
-
或是使指针指向现有的内存,或者给他动态分配内存,否则我们并不知道指针指向哪儿,这将是一个很严重的问题。
-
new:C++中new运算符用于动态分配内存的运算符。 -
delete: 释放new分配的单个对象指针指向的内存//动态申请一个变量 int *p =new int;//定义int型指针变量p,并指向一个int大小的内存地址 int *pp =new int(3);//定义int型指针变量pp,并指向一个int大小的内存地址,初始化值为3 delete p;//释放p指向的动态地址,收归系统所有,成为自由内存 p = NULL;//p指向空指针,这是一个好习惯,不然p会变为野指针 //申请一个动态数组 int n=10,*p = new int[n];//动态申请n个元素的数组 for(int i=0;i<n;++i) printf("%d ",p[i]); delete[] p;//释放p指向的动态地址,收归系统所有,成为自由内存 p=NULL; //申请一个结构体变量 struct Node{ char name[10]; int age; }; Node *p = new Node;//申请一个结构体变量p并分配内存 p->name="Tom";//成员变量赋值 delete p;//
-
-
没有合法指向的指针称为“野”指针。因为“野”指针随机指向一块空间,该空间中存储的可能是其他程序的数据甚至是系统数据,故不能对“野”指针所指向的空间进行存取操作,否则轻者会引起程序崩溃,严重的可能导致整个系统崩溃。
-
-
int a,*p=&a; //用变量a的内存地址初始化 int *a=3;//错误,a是野指针,直接赋值可能导致严重后果 int a,b,*pa,*pb; char *pc,c; pa=&a;//正确。pa基类型为int,a为int型变量,类型一致 pb=&c;//错误。pb基类型为int,c为char型变量,类型不一致 pb=pa;//正确。同类型的指针变量可以相互赋值。 pc=&c;//正确。pc基类型为char,c为char型变量,类型一致 *pa=&a;//错误。指针变量是pa而非*pa -
指针变量是专门保存地址值(指针)的变量,我们把指针变量形象地看成“地址箱”。
int a=3,*pa=&a; //pa保存变量a的地址,即指向a char c='d',*pc=&c; //pc保存变量c的地址,即指向c-
把整型变量
a的地址赋给地址箱pa,即pa指向变量a,同理pc指向变量c,如图 2 所示。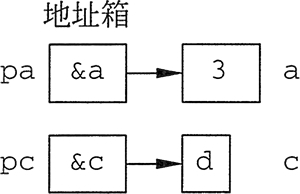
-
10.2.4 指针变量的引用
-
访问内存空间,一般分为直接访问和间接访问。
-
直接访问:如果知道内存空间的名字,可通过名字访问该空间,称为直接访问。通过变量名操作变量,也就是通过名字直接访问该变量对应的内存单元。
-
间接访问:如果知道内存空间的地址,也可以通过该地址间接访问该空间。通过指针访问内存空间是间接访问
-
对内存空间的访问操作一般指的是存、取操作,即向内存空间中存入数据和从内存空间中读取数据。
-
在 C++ 语言中,可以使用间接访问符(间接访问操作符)*来访问指针所指向的空间。
int a=3,*p=&a;//p中保存变量a对应内存单元的地址 printf("a=%d\n",a); //通过名字,直接访问变量a空间(读取) printf("a=%d\n",*p); //通过地址,间接访问变量a空间(读取) *p=6;//等价于a=6;间接访问a对应空间(存)- 注意
*在定义变量时是表示变量为指针变量,在使用时表示指针所存储的地址里的值,即相当于变量。
- 注意
10.2.5 空指针
-
指向空,或者说不指向任何东西。 在C++中,
NULL实质是0。 -
换种说法:任何程序数据都不会存储在地址为
0的内存块中,它是被操作系统预留的内存块。int *p = NULL;//正确,强烈建议如果指针定义时没有具体指向,请指向NULL *p = 10;//错误!系统不允许对空指针进行操作
10.2.6 指针的运算
-
指针的算术运算只限于两种形式:
-
指针
+,-,++,--等操作,所得结果也是一个指针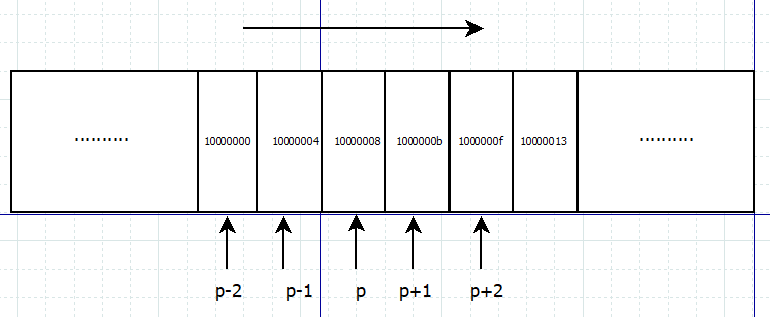
-
指针 - 指针
-
只有当两个指针都指向同一个数组中的元素时,才允许从一个指针减去另一个指针。
-
两个指针相减的结果的类型是 ptrdiff_t,它是一种有符号整数类型。
-
减法运算的值是两个指针在内存中的距离(以数组元素的长度为单位,而不是以字节为单位)
int a[10] = {1,2,3,4,5,6,7,8,9,0}; int sub,*p1 = &a[2],*p2 = &a[8]; sub = p2-p1; printf("%d\n",sub); // 输出结果为 6
-
-
10.2.7 指针与数组
-
指针变量加 1 表示跳过该指针变量对应的基类型所占字节数大小的空间。
-
数组元素访问的三种方式:
-
直接访问:数组名[下标]; 的形式。如
a[3]。 -
间接访问:*(数组名+
i); 的形式。其中,i为整数,其范围为:0<=i<N,N为数组大小。for(int i=0;i<n;++i) printf("%d ",*(a+i));//等价与a[i] -
间接访问:*(指针变量);的形式。
int a[10],*p; p = a;//等价与 p = &a[0]; //方法一: for(int i=0;i<10;++i) printf("%d ",*(p+i));//等价*(a+i) //方法二: for(int i=0;i<10;++i) printf("%d ",p[i]);//等价a[i] //方法三: for(p=a;p<a+10;++p) printf("%d ",*p);- 数组名
a相当于数组首元素a[0]的地址,即a等价于&a[0]。
- 数组名
-
10.2.8 指针与结构体
-
当一个指针变量指向结构体时,我们就称它为结构体指针。C++语言结构体指针的定义形式一般为:
struct 结构体名 *变量名;//可以省略关键字struct struct stu{ char *name; //姓名 int num; //学号 int age; //年龄 char group; //所在小组 float score; //成绩 } stu1 = { "Tom", 12, 18, 'A', 136.5 }; struct stu *p = &stu1;//或者stu *pstu = &stu1; -
获取结构体成员
-
通过结构体指针可以获取结构体成员,一般形式为:
-
(*pointer).memberName.运算符的优先级高于*,小括号必不可少
-
pointer->memberName->是一个新的运算符,习惯称它为“箭头”,有了它,可以通过结构体指针直接取得结构体成员;这也是->在C语言中的唯一用途。
printf("%s %d\n",(*p).name,(*p).num);//方法一 printf("%s %d\n",p->name,p->num);//方法二,推荐使用
-
-
10.2.9 指针例题
-
约瑟夫问题代码
struct person{ int num; person *next; }; person *Circle(int n){//创建约瑟夫环并返回头指针 person *head = new person; head->num=1;//初始化第一个点 head->next=NULL;//置空 person *p = head;//定义一个临时指针,做连接用 for(int i=2;i<=n;++i){ person *q = new person; q->num=i;q->next=NULL; p->next=q;//上个结点和当前结点相连 p=q;//指向当前结点 } p->next=head;//首尾相连 return head;//返回头指针 } void ysf(person *head,int k){//数到k出圈 person *tail,*p=head;//指向报数的位置 while(p->next!=p){//相等说明环上只有一个人了 //p记录报k的位置,tail记录报k-1,方便做删除操作。 for(int i=1;i<k;++i){ tail=p; p=p->next; }//跳出循环p指向报k的人,tail指向报k-1的人 tail->next=p->next;//把p的上一个和下一个相连 printf("%d ",p->num); delete p;//释放动态内存p p=tail->next; } printf("%d ",p->num);//输出最后出列的人 delete p; } void Solve(){ int n,k;scanf("%d%d",&n,&k); person *head=Circle(n); ysf(head,k); } int main(){ Solve(); return 0; }
10.3 树结构的存储
-
我们表示一棵树的方法有:双亲表示法,孩子表示法,孩子兄弟表示法
-
双亲表示法
-
以双亲作为索引的关键词的一种存储方式
-
每个结点只有一个双亲,所以选择顺序存储占主要
-
结点定义:
struct Node{ char data;//存储值 int parent;//存储结点的父亲结点编号 }a[maxn];//结点个数maxn -
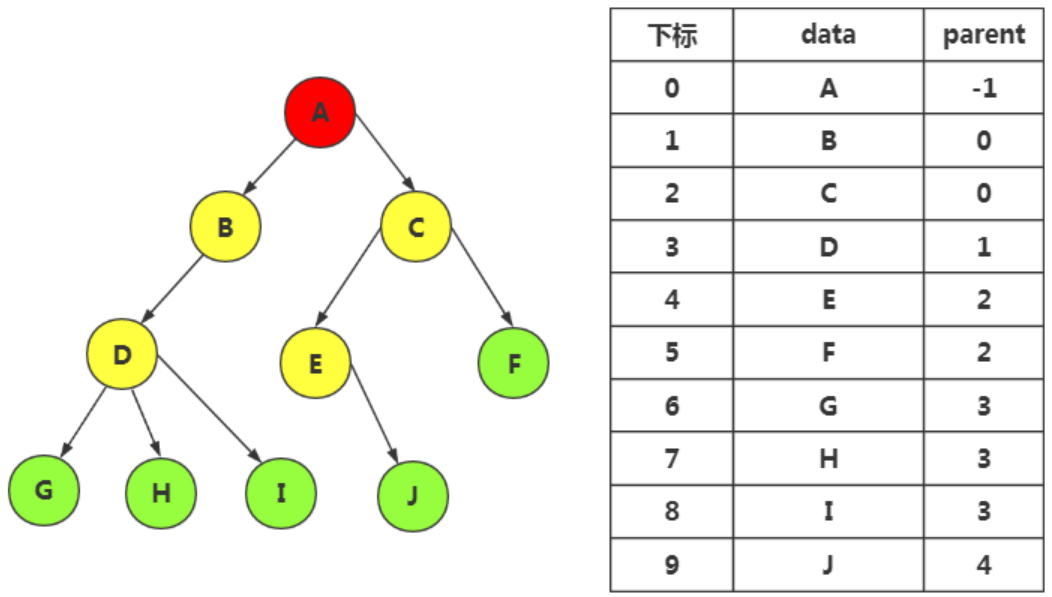
-
优缺点分析:
- 优点:
parent指针域指向数组下标,所以找双亲结点的时间复杂度为O(1),向上一直找到根结点也快 - 缺点:由上向下找就十分慢,若要找结点的孩子或者兄弟,要遍历整个树
- 优点:
-
-
孩子表示法
-
由于每个结点可有多个子树,所以我们用树的度数来定义每个结点的孩子数
-
结点定义:
struct Node{ char data;//存储值 int child[max_d];//树的度数是max_d }a[maxn];//结点个数maxn -
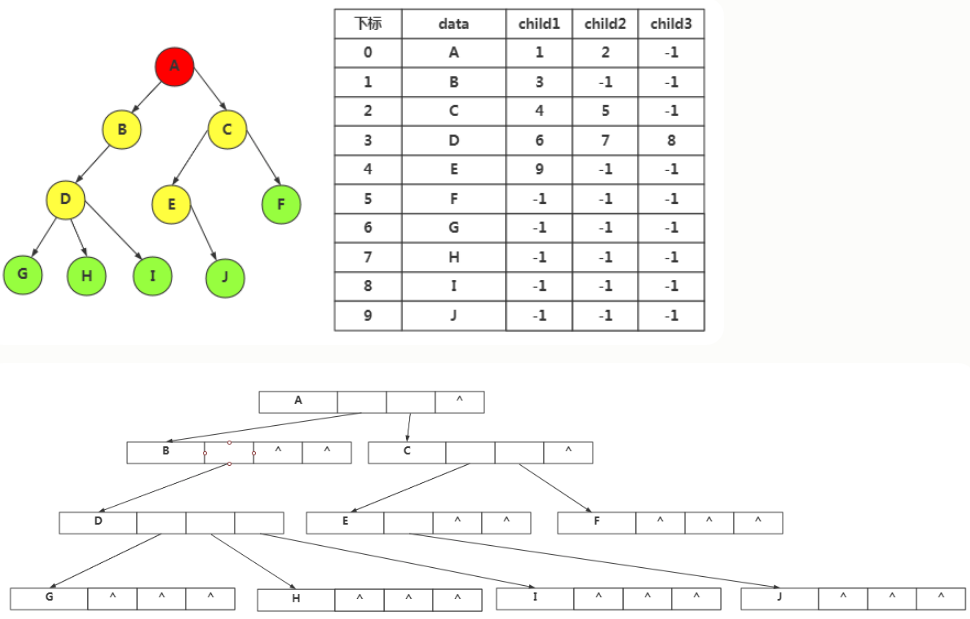
-
优缺点分析:
- 占用了大量不必要的孩子域空指针
- 以其为标准:需要
3n个指针域,实际上有用n-1个(除了根结点,其他n-1个都向上需要一条边),则有2n+1个无用
-
-
孩子兄弟表示法
-
任意一棵树,他的结点的第一个孩子如果存在就是唯一结点,他的右兄弟如果存在,也是唯一的,因此,我们设置两个指针,分别指向该结点的第一个孩子和该结点的右兄弟
-
结点定义:
struct Node{ char data;//存储值 Node *Firstchild,*Rightbrother; }a; -
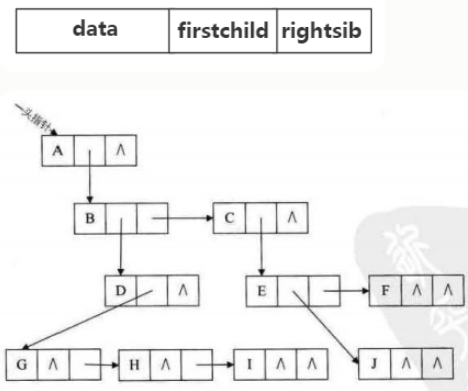
-
优缺点分析:
n个结点,有2n个指针域,有n-1条边,空n+1个指针域- 相对来说空间还是比较节约,如有需要可转成二叉树处理。
-
-
10.4 二叉树
10.4.1 二叉树的定义
-
二叉树是n(n>=0)个结点的有限集合,该集合或者为空集(称为空二叉树),或者由一个根结点和两棵互不相交的、分别称为根结点的左子树和右子树组成。
10.4.2 满二叉树
-
满二叉树:在一棵二叉树中。如果所有分支结点都存在左子树和右子树,并且所有叶子都在同一层上,这样的二叉树称为满二叉树。
-
满二叉树的特点有:
- 叶子只能出现在最下一层。出现在其它层就不可能达成平衡。
- 非叶子结点的度一定是
2。 - 在同样深度的二叉树中,满二叉树的结点个数最多,叶子数最多。

10.4.3 完全二叉树
-
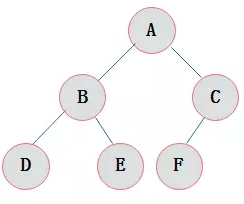
完全二叉树:对一颗具有
n个结点的二叉树按层编号,如果编号为i(1<=i<=n)的结点与同样深度的满二叉树中编号为i的结点在二叉树中位置完全相同,则这棵二叉树称为完全二叉树。 -
下图展示一棵完全二叉树
-
完全二叉树的特点
- 叶子结点只能出现在最下层和次下层。
- 最下层的叶子结点集中在树的左部。
- 倒数第二层若存在叶子结点,一定在右部连续位置。
- 如果结点度为
1,则该结点只有左孩子,即没有右孩子。 - 同样结点数目的二叉树,完全二叉树深度最小。
- 在完全二叉树中,具有n个结点的完全二叉树的深度为\([log_2n]+1\),其中\([log_2n]\)是向下取整。
- 若对含
n个结点的完全二叉树从上到下且从左至右进行1至n的编号,则对完全二叉树中任意一个编号为i的结点有如下特性:- 若
i=1,则该结点是二叉树的根,无双亲, 否则,编号为[i/2]的结点为其双亲结点; - 若
2*i>n,则该结点无左孩子, 否则,编号为2*i的结点为其左孩子结点; - 若
2*i+1>n,则该结点无右孩子结点, 否则,编号为2*i+1的结点为其右孩子结点。
- 若
注:满二叉树一定是完全二叉树,但反过来不一定成立。
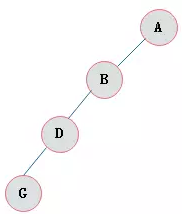
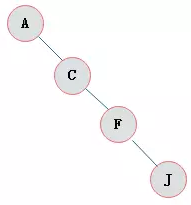
10.4.4 斜树
- 所有的结点都只有左子树的二叉树叫左斜树。所有结点都是只有右子树的二叉树叫右斜树。这两者统称为斜树。
10.4.5 二叉树性质
- 每个结点最多有两颗子树,所以二叉树中不存在度大于2的结点。
- 左子树和右子树是有顺序的,次序不能任意颠倒。
- 即使树中某结点只有一棵子树,也要区分它是左子树还是右子树。
- 在二叉树的第
i层上最多有 \(2^{i-1}\) 个结点 。(\(i\ge 1\)) - 二叉树中如果深度为
k,那么最多有\(2^k-1\)个结点。(\(k>=1\)) - \(n_0=n_2+1 , n_0\)表示度数为
0的结点数,\(n_2\)表示度数为2的结点数。- 证明:
- 二叉树中所有结点的度数均不大于2,令结点总数为:
n,度数为0,1,2结点数:\(n_0,n_1,n_2\),则:- \(n=n_0+n_1+n_2\) ……(式子1)
- 度为
1的结点有一个孩子,度为2结点有两个孩子,故二叉树中孩子结点总数是:- \(n_1+2*n_2\)
- 树中只有根结点不是任何结点的孩子,故二叉树中的结点总数又可表示为:
- \(n=n_1+2*n_2+1\) ……(式子2)
- 由式子1和式子2得到:
- \(n_0=n_2+1\)
- 二叉树中所有结点的度数均不大于2,令结点总数为:
- 证明:
10.4.6 二叉树的存储
-
顺序存储
-
二叉树的顺序存储结构就是使用一维数组存储二叉树中的结点,并且结点的存储位置,就是数组的下标索引。
-
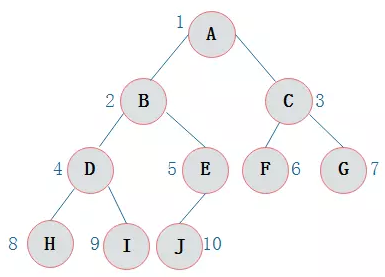
-

-
由上图可以看出,当二叉树为完全二叉树时,结点数刚好填满数组。那么当二叉树不为完全二叉树时,采用顺序存储形式如何呢?


- 其中浅色结点表示结点不存在。其中,∧表示数组中此位置没有存储结点。此时可以发现,顺序存储结构中已经出现了空间浪费的情况。
- 最坏的情况,比如右斜树

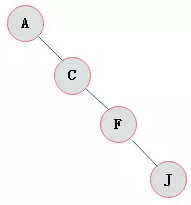

- 顺序存储一般适用于完全二叉树。
-
-
二叉链表
-
由二叉树定义可知,二叉树的每个结点最多有两个孩子。因此,可以将结点数据结构定义为一个数据和两个指针域。
struct Node{ char data;//数据 Node *lchild,*rchild; }; -
存储结构如下图所示
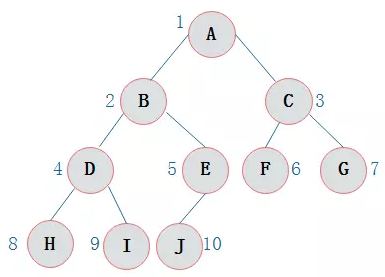
-
10.4.7 二叉树遍历
-
二叉树的遍历是指从二叉树的根结点出发,按照某种次序依次访问二叉树中的所有结点,使得每个结点被访问一次,且仅被访问一次。
-
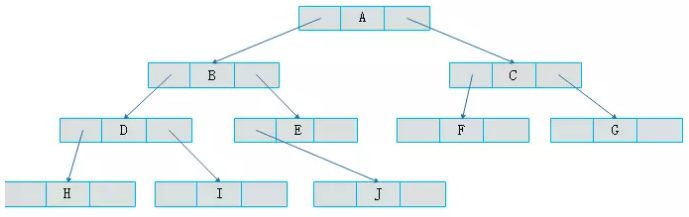
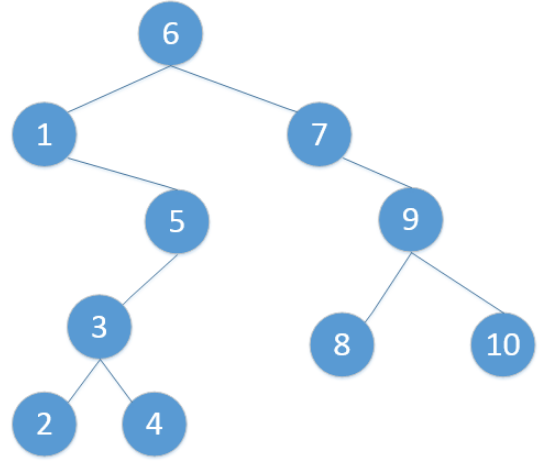
二叉树的访问次序可以分为四种:前序遍历、中序遍历、后序遍历、层序遍历
- 前序遍历
- 先访问根结点,再从左到右按照前序遍历思想递归遍历各棵子树。
- 上图前序遍历的结果为:
ABDHIEJCFG- 从根结点出发,则第一次到达结点
A,故输出A; - 继续向左访问,第一次访问结点
B,故输出B; - 按照同样规则,输出
D,输出H; - 当到达叶子结点
H,返回到D,此时D的左子树已访问结束,进而访问D的右子树I; - 按照同样的访问规则,继续输出
E,J,C,F,G;
- 从根结点出发,则第一次到达结点
- 中序遍历
- 先遍历左子树,再访问根结点,再遍历右子树。
- 上图中序遍历的结果为:
HDIBJEAFCG- 从根结点出发,访问结点A,
A存在左子树B,则递归访问左子树B,依次递归直到H; - 到达
H,H左子树为空,则输出结点H,访问H右子树,为空,返回H子树根结点D; - 返回至
D,此时D的左子树访问完毕,输出D,访问D的右子树I; - 结点
I左子树为空,则输出I,右子树为空则返回父结点D; - 按照同样规则继续访问,输出
B,J,E,A,F,C,G;
- 从根结点出发,访问结点A,
- 后序遍历
- 先从左到右遍历各棵子树,再访问根结点。
- 上图后序遍历的结果为:
HIDJEBFGCA- 从根结点
A出发,A左右子树非空,先递归访问左子树B - 以此类推到达
H,H左、右子树为空,则输出H; - 由
H返回至D,D左子树访问结束,递归访问其右子树I; I左右子树均为空,输出I;- 返回至
D,此时D左、右子树均访问结束,故输出D; - 按照同样规则继续访问,输出
J,E,B,F,G,C,A;
- 从根结点
- 层次遍历:
- 按层次从小到大逐个访问,同一层次按照从左到右的次序。
- 上图层次遍历的结果为:
ABCDEFGHIJ
10.4.8 例题
10.4.8.1 树的遍历
-
【问题描述】
- 给出一个
n个结点的二叉树,请求出二叉树的前序遍历,中序遍历和后序遍历。 -

- 给出一个
-
【输入格式】
- 第一位一个整数
n(0<n<=26),表示二叉树有n个结点,结点序号:\(1\sim n\)。 - 以下
n行,第i行表示序号为i的结点信息,第一个大写字母表示结点的值,后面为两整数,第一个表示左儿子序号,第二个表示右儿子序号,如果该序号为0表示没有,结点1为根结点。
- 第一位一个整数
-
【输出格式】
- 共三行,第一行为二叉树的前序遍历,第二行为中序遍历,第三行为后序遍历
-
【输入样例】
7 F 2 3 C 4 5 E 0 6 A 0 0 D 7 0 G 0 0 B 0 0 -
【样例输出】
FCADBEG ACBDFEG ABDCGEF -
代码实现
#include <bits/stdc++.h> const int maxn=26+5; struct Node{//结点 char data;//值 int lch,rch;//记录结点左右儿子序号 }a[maxn]; int n; void Head_s(int x){//前序遍历 if(x==0)return; printf("%c",a[x].data);//先输出根结点 Head_s(a[x].lch);//再递归访问左子树 Head_s(a[x].rch);//再递归访问右子树 } void Mid_s(int x){//中序遍历 if(x==0)return; Mid_s(a[x].lch);//先遍历左子树 printf("%c",a[x].data);//左子树访问结束,输出根结点 Mid_s(a[x].rch);//再递归访问右子树 } void Tail_s(int x){//后序遍历 if(x==0)return; Tail_s(a[x].lch);//先遍历左子树 Tail_s(a[x].rch);//再遍历右子树 printf("%c",a[x].data);//左右子树访问结束,输出根结点 } void Solve(){ scanf("%d",&n); for(int i=1;i<=n;++i) scanf(" %c%d%d",&a[i].data,&a[i].lch,&a[i].rch); Head_s(1);printf("\n"); Mid_s(1);printf("\n"); Tail_s(1);printf("\n"); } int main(){ Solve(); return 0; }
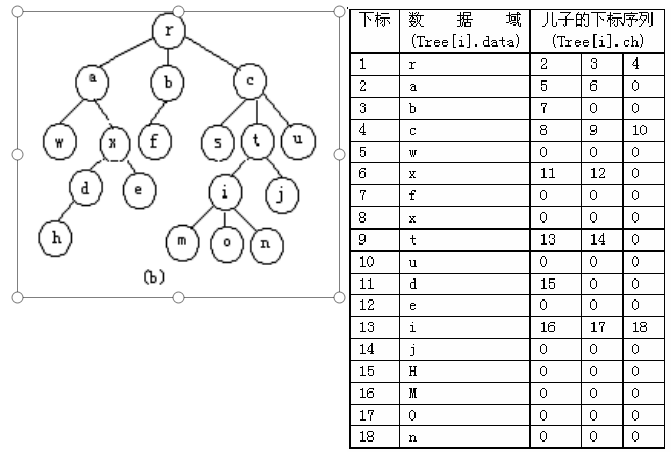
10.4.8.2 普通树转二叉树
-
Description
- 输入一棵普通有序树,先把树转成二叉树,然后输出该树的先根次序和后根次序。
-
Input
- 第一行为顶点个数\(n(1≤n≤26)\)。
- 以下含\(n\)行,其中第\(i\)行\((1≤i≤n)\)的元素依次为结点\(i\)的数据值\(a_i\)(为一个小写字母)。以后各元素为结点\(i\)的儿子序列,以0结束。
- 若\(a_i\)后仅含一个\(0\),则说明结点\(i\)为叶子。
-
Output
- 输出共两行,第一行该树的前序遍历,第二行为后续遍历,结点间没有空格
-
Sample Input
18 r 2 3 4 0 a 5 6 0 b 7 0 c 8 9 10 0 w 0 x 11 12 0 f 0 s 13 14 0 t 0 u 0 d 15 0 e 0 i 16 17 18 0 j 0 h 0 m 0 o 0 n 0 -
Sample Output
rawxdhebfcsimonjtu hedxwfnomjiutscbar -
分析:
-
普通树为有序树
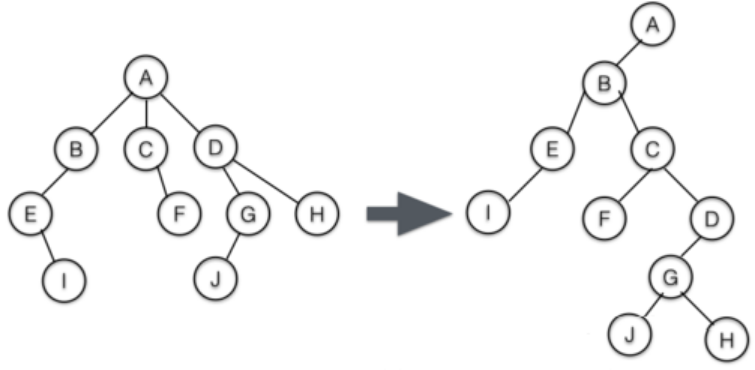
T,将其转化成二叉树T‘的规则如下:-
T中的结点与T’中的结点一一对应,即T中每个结点的序号和值在T’中保持不变; -
T中某结点v的第一个儿子结点为\(v_1\),则在T’中\(v_1\)为对应结点v的左儿子结点; -
T中结点v的儿子序列,在T’中被依次链接成一条开始于\(v_1\)的右链; -
口诀:左儿子不变,兄弟边右儿子!
-
-
-
代码实现
#include <bits/stdc++.h> const int maxn=26+10; struct Tree{//结点 char data;//值 int lch,rch;//左、右子树编号 }a[maxn]; void Build_tree(); void Pre_order(int); void Succ_order(int); int main(){ Build_tree(); Pre_order(1);printf("\n"); Succ_order(1);printf("\n"); return 0; } void Build_tree(){//建树 int n;scanf("%d",&n); for(int i=1;i<=n;++i){ scanf(" %c",&a[i].data); int j,p;scanf("%d",&j);//读i结点的第一个儿子结点编号 if(j==0)continue;//i是叶子结点 a[i].lch=j;p=j;//第一个结点为i的左儿子,p存储当前结点 while(j){//当存在儿子结点 scanf("%d",&j);//读入下一个结点编号 a[p].rch=j;p=j;//当前结点是上一个结点的右儿子 } } } void Pre_order(int x){//前序遍历 if(x==0)return; printf("%c",a[x].data); Pre_order(a[x].lch); Pre_order(a[x].rch); } void Succ_order(int x){//后序遍历 if(x==0)return; Succ_order(a[x].lch); Succ_order(a[x].rch); printf("%c",a[x].data); }
10.5 二叉搜索树
10.5.1 定义
-
二叉搜索树又称二叉查找树,亦称为二叉排序树。
-
若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值;
-
若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值;
-
它的左、右子树也分别为二叉排序树。
10.5.2 二叉搜索树的插入
-
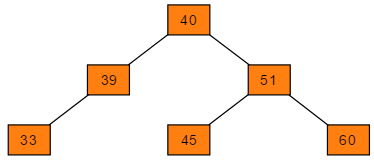
现有序列:
A = {61, 87, 59, 47, 35, 73, 51, 98, 37, 93}。根据此序列构造二叉搜索树过程如下:-
i = 0,A[0] = 61,结点61作为根结点; -
i = 1,A[1] = 87,87 > 61,且结点61右孩子为空,故81为61结点的右孩子; -
i = 2,A[2] = 59,59 < 61,且结点61左孩子为空,故59为61结点的左孩子; -
i = 3,A[3] = 47,47 < 59,且结点59左孩子为空,故47为59结点的左孩子; -
i = 4,A[4] = 35,35 < 47,且结点47左孩子为空,故35为47结点的左孩子; -
i = 5,A[5] = 73,73 < 87,且结点87左孩子为空,故73为87结点的左孩子; -
i = 6,A[6] = 51,47 < 51,且结点47右孩子为空,故51为47结点的右孩子; -
i = 7,A[7] = 98,98 < 87,且结点87右孩子为空,故98为87结点的右孩子; -
i = 8,A[8] = 37,37 > 33,且结点33右孩子为空,故37为33结点的右孩子; -
i = 9,A[9] = 93,93 < 98,且结点98左孩子为空,故93为98结点的左孩子;创建完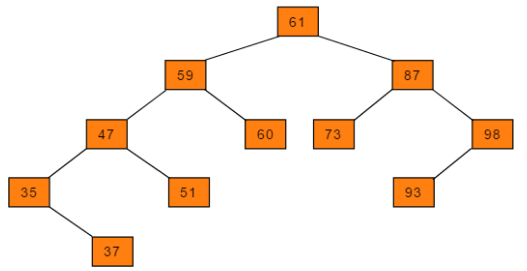
-
-
代码实现
//二叉树的创建过程实际上就是插入过程 #include <cstdio> #include <cstring> const int maxn = 10000 + 5; struct Node{//结点定义 int data; Node *lch,*rch; Node(){//构造函数初始化 data=0;lch=NULL,rch=NULL; } }; Node *Bst_build(Node *t,int key){//递归插入,并返回根结点的值 if(t==NULL){//结点为空创建新的结点,并值域赋值 t=new Node; t->data=key; } else{ if(key<t->data)//递归左子树,并返回子结点为其左儿子 t->lch=Bst_build(t->lch,key); else//递归右子树,并返回子结点为其右儿子 t->rch=Bst_build(t->rch,key); } return t;//返回当前子树的根结点 } Node *Bst_insert(Node *root,int key){//非递归 if(root==NULL){//如果根结点不存在,创建根 root=new Node; root->data=key; return root;//返回根结点 } Node *p,*q=root;//存在根,则从根往下找key所在位置 while(q){//当q不为空 p=q;//p存储当前结点 if(key < q->data) q=q->lch; else//等于key也放在了右子树 q=q->rch; }//跳出循环q为空,p指向q的父亲结点 q=new Node;//为q结点分配地址,并赋值 q->data=key; //不知道q是p的左儿子还是右儿子,所以还需判断 if(key < p->data) p->lch=q; else p->rch=q; return root; } void Mid_s(Node *t){//中序遍历 if(t==NULL)return; Mid_s(t->lch); printf("%d ",t->data); Mid_s(t->rch); } void Solve(){ int n;scanf("%d",&n); Node *Tree=NULL;//创建根结点,但并为分配地址 for(int i=1;i<=n;++i){ int key;scanf("%d",&key); Tree=Bst_insert(Tree,key);//没读入一个数就从根结点往下递归插入 } Mid_s(Tree);//中序遍历相当于对序列升序排列 } int main(){ Solve(); return 0; }
10.5.3 二叉搜索树的查找
-
查找流程:
- 如果树是空的,则查找结束,无匹配,返回空指针。
- 如果被查找的值和结点的值相等,查找成功,返回结点指针。
- 如果被查找的值小于结点的值,递归查找左子树
- 如果被查找的值大于结点的值,递归查找右子树,
-
代码实现
Node *Bst_find(Node *root,int key){ if(root==NULL || root->data==key) return root;//找到找不到都返回root if(key < root->data)//递归左子树 return Bst_find(root->lch,key); else//递归右子树 return Bst_find(root->rch,key); }
10.5.4 二叉搜索树的前驱和后继
-
二叉树的结点的值是按照二叉树中序遍历顺序连续设定。
-
-
前驱结点
-
若一个结点有左子树,那么该结点的前驱结点是其左子树中值最大的结点
-
若一个结点没有左子树,那么判断该结点和其父结点的关系
- 若该结点是其父结点的右孩子,那么该结点的前驱结点即为其父结点。
- 若该结点是其父结点的左孩子,那么需要沿着其父亲结点一直向树的顶端寻找,直到找到一个结点
P,P结点是其父结点Q的右边孩子(可参考上图2的前驱结点是1),那么Q就是该结点的后继结点
-
二叉搜索树值最小的结点没有前驱结点
-
代码实现
Node *Precursor(Node *root){//前驱,记住单词! Node *p=root; if(p->lch){//如果root存在左子树,则为左子树中最大值 p=p->lch; while(p->rch)//最大值就是一直往右 p=p->rch; return p;//跳出循环时p右子树为NULL,p即为左子树最大值 } else{//如果root没有左儿子,只能从祖先结点去找了 Node *q=root->prt; while(q && p==q->lch){//如果p有父结点,且是其左儿子,一直往上找 p=q;q=q->prt; } //跳出循环时可能q==NULL,此时说明root为树的最小结点,没有前驱 //或者q!=NULL,此时p是q的右儿子,q即为root的前驱 return q; } }
-
-
后继结点
-
若一个结点有右子树,那么该结点的后继结点是其左子树中值最小的结点
-
若一个结点没有右子树,那么判断该结点和其父结点的关系
- 若该结点是其父结点的左儿子,那么该结点的后继结点即为其父结点。
- 若该结点是其父结点的右儿子,那么需要沿着其父亲结点一直向树的顶端寻找,直到找到一个结点
P,P结点是其父结点Q的左儿子(可参考上图4的前驱结点是5),那么Q就是该结点的后继结点
-
二叉搜索树值最大的结点没有后继结点
-
代码实现
Node *Successor(Node *root){//单词,林思旭,你记住了吗 :)? Node *p=root; if(p->rch){//如果root有右子树 p=p->rch;//查找右子树的最小值,即一直向左! while(p->lch) p=p->lch; return p; } else{//如果root没有右子树,则后继在其祖先结点,root在其祖先结点的左子树上 Node *q=root->prt; while(q && (p==q->rch)){ p=q;q=q->prt; } //跳出循环时可能q==NULL,此时说明root为树的最大结点,没有后继 //或者q!=NULL,此时p是q的左儿子,q即为root的前驱 return q; } }
-
10.5.5 二叉搜索树的删除
-
删除叶子结点
-
删除叶子结点的方式最为简单,只需查找到该结点,直接删除即可。
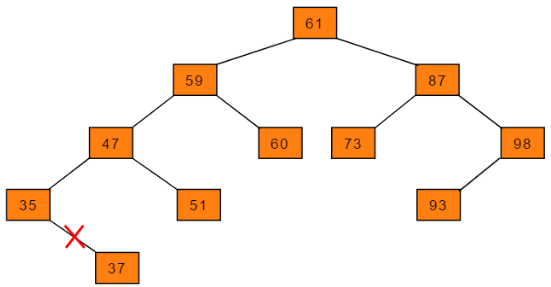
- 上图中的叶子结点37、结点51、结点60、结点73和结点93的方式是相同的。
-
-
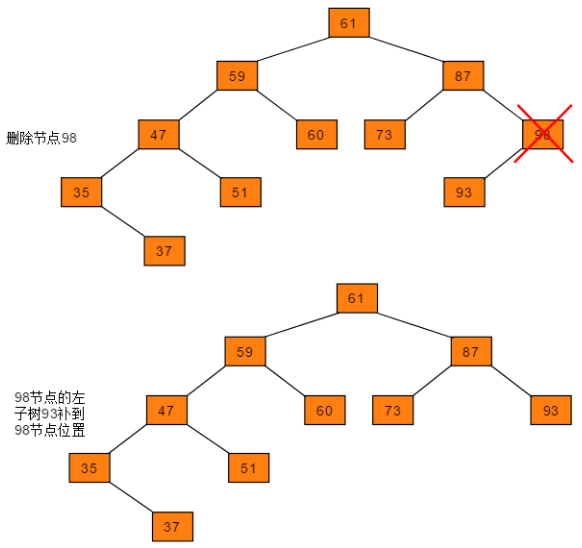
删除的结点只有左子树
- 删除的结点若只有左子树,将结点的左子树替代该结点位置。
-
删除的结点只有右子树
- 删除的结点若只有右子树,将结点的右子树替代该结点位置。这种情况与删除左子树处理方式类似,不再赘述。
-
删除的结点既有左子树又有右子树。
- 若删除的结点既有左子树又有右子树,这种结点删除过程相对复杂。其流程如下:
- 遍历待删除结点的左子树,找到其左子树中的最大结点,即删除结点的前驱结点;
- 将最大结点代替被删除结点;
- 删除左子树中的最大结点;
- 左子树中待删除最大结点一定为叶子结点或者仅有左子树。按照之前情形删除即可。
- 若删除的结点既有左子树又有右子树,这种结点删除过程相对复杂。其流程如下:
-
二叉搜索树删除
Node *Del(Node *root,int key){ if(root==NULL)//如果找不到即返回空 return NULL; if(key < root->data) root->lch = Del(root->lch,key); else if(key > root->data) root->rch = Del(root->rch,key); else{//如果root->data==key,即为删除的结点 if(!root->lch || !root->rch){//如果root的左右子树只要有一个为空 Node *temp=root;//记录root所指向内存 root=root->lch ? root->lch : root->rch;//左子树不空,左子树替换右子树,否则右子树替换,如果左右子树均为空则相当于删除了结点,不过没有处理内存释放问题 delete temp;//释放删除结点内存 } else{//左右子树均存在 Node *p; for(p=root->lch;p->rch;p=p->rch);//循环结束时p为root的前驱 root->data=p->data;//修改p的值为q的值,其他关系不变 root->lch=Del(root->lch,p->data); } } return root; }
10.6 二叉堆
- 堆(
heap),这里所说的堆是数据结构中的堆,而不是内存模型中的堆。堆通常是一个可以被看做一棵树,它满足下列性质:- 堆中任意结点的值总是不大于(不小于)其子结点的值;
- 堆总是一棵完全树。
- 将任意结点不大于其子结点的堆叫做最小堆或小根堆,而将任意结点不小于其子结点的堆叫做最大堆或大根堆。常见的堆有二叉堆、左倾堆、斜堆、二项堆、斐波那契堆等等。
10.6.1 二叉堆的定义
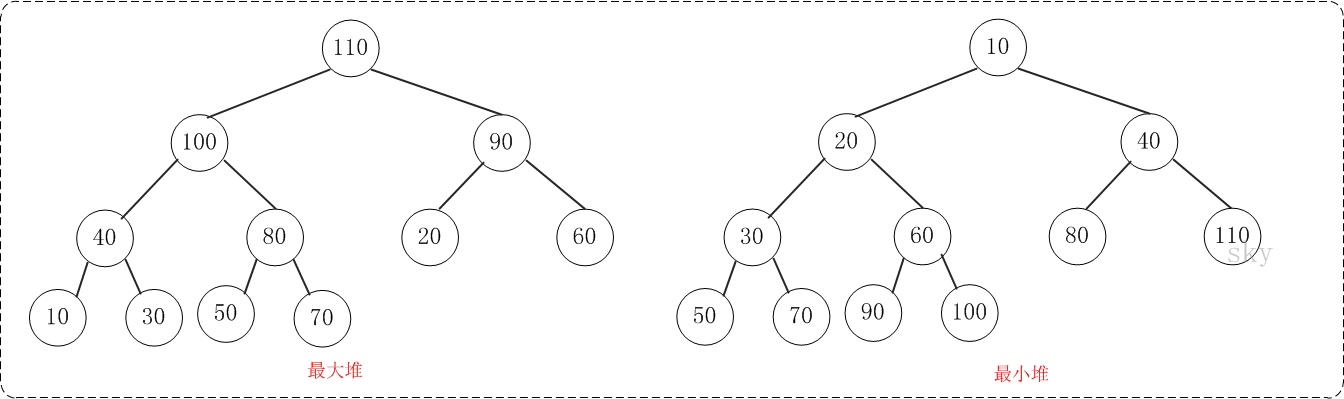
-
二叉堆是完全二叉树或者是近似完全二叉树,它分为两种:大根堆和小根堆。
-
大根堆:父结点的键值总是大于或等于任何一个子结点的键值;
-
小根堆:父结点的键值总是小于或等于任何一个子结点的键值。
-
示意图如下:
-
10.6.2 二叉堆的存储
- 二叉堆一般都通过"数组"来实现。数组实现的二叉堆,父结点和子结点的位置存在一定的关系。
- 我们将"二叉堆的第一个元素"放在数组索引
0的位置,有时候放在1的位置。当然,它们的本质一样(都是二叉堆),只是实现上稍微有一丁点区别。- 假设"第一个元素"在数组中的索引为
0的话,则父结点和子结点的位置关系如下:- 索引为
i的左孩子的索引是(2*i+1); - 索引为
i的右孩子的索引是(2*i+2); - 索引为
i的父结点的索引是floor((i-1)/2);
- 索引为
- 假设"第一个元素"在数组中的索引为
1的话,则父结点和子结点的位置关系如下:- 索引为
i的左孩子的索引是(2*i); - 索引为
i的右孩子的索引是(2*i+1); - 索引为
i的父结点的索引是floor(i/2);
- 索引为
- 假设"第一个元素"在数组中的索引为
10.6.3 二叉堆的插入
-
假设在最大堆
{90,80,70,60,40,30,20,10,50}种添加85,需要执行的步骤如下: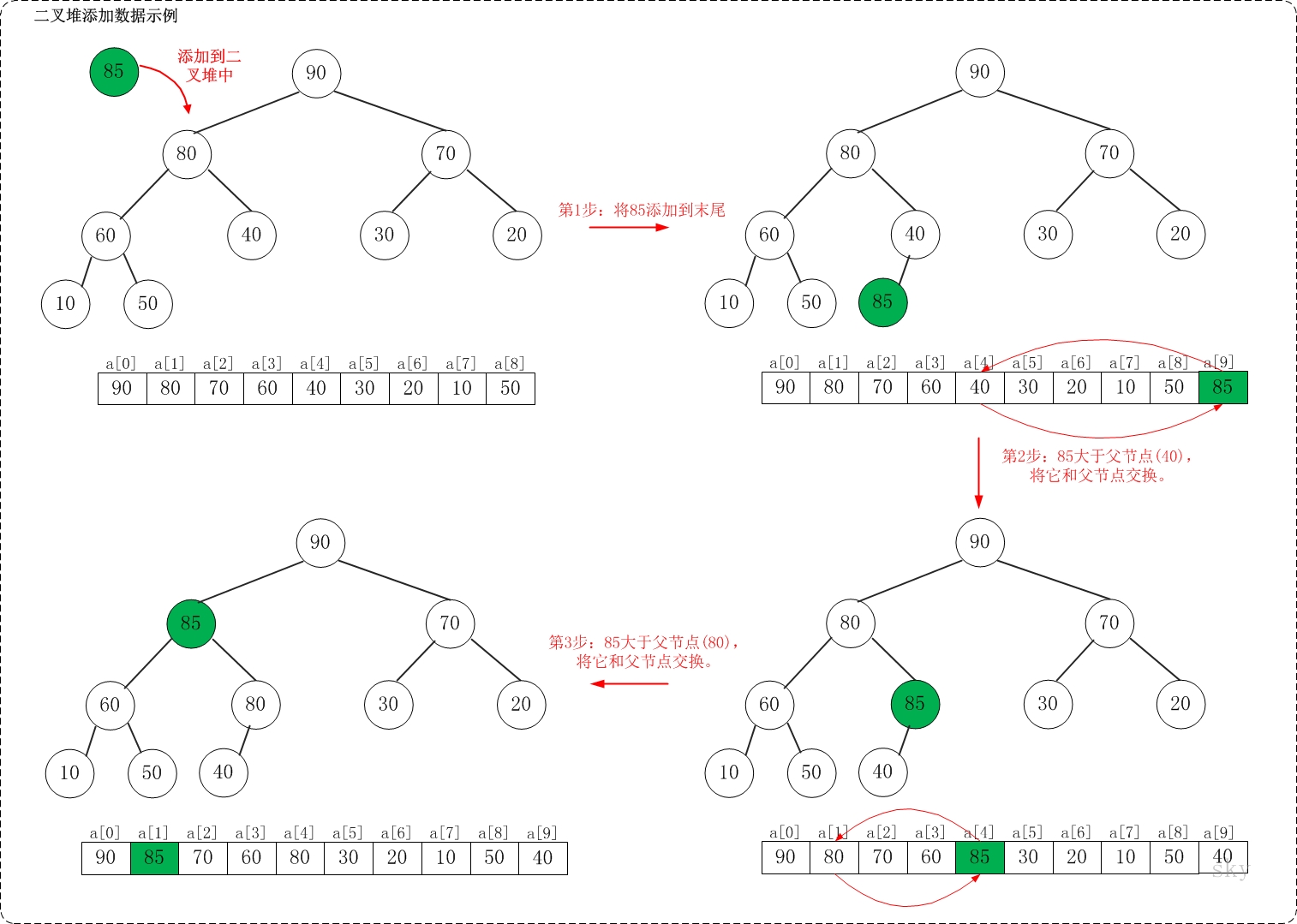
-
首先将待插入元素追加到数组尾部
-
然后将其进行上滤操作,也就是将其与父结点比较,如果大于父结点就交换,直到小于等于父结点或者到达根。
-
代码实现
void Push(int x){ Heap[++siz]=x;//把插入的元素x放在数组最后 for(int i=siz;i/2>0 && Heap[i]>Heap[i/2];i=i/2) swap(Heap[i],Heap[i/2]); }
-
10.6.4 二叉堆的删除
-
假设从最大堆
{90,85,70,60,80,30,20,10,50,40}中删除90,需要执行的步骤如下: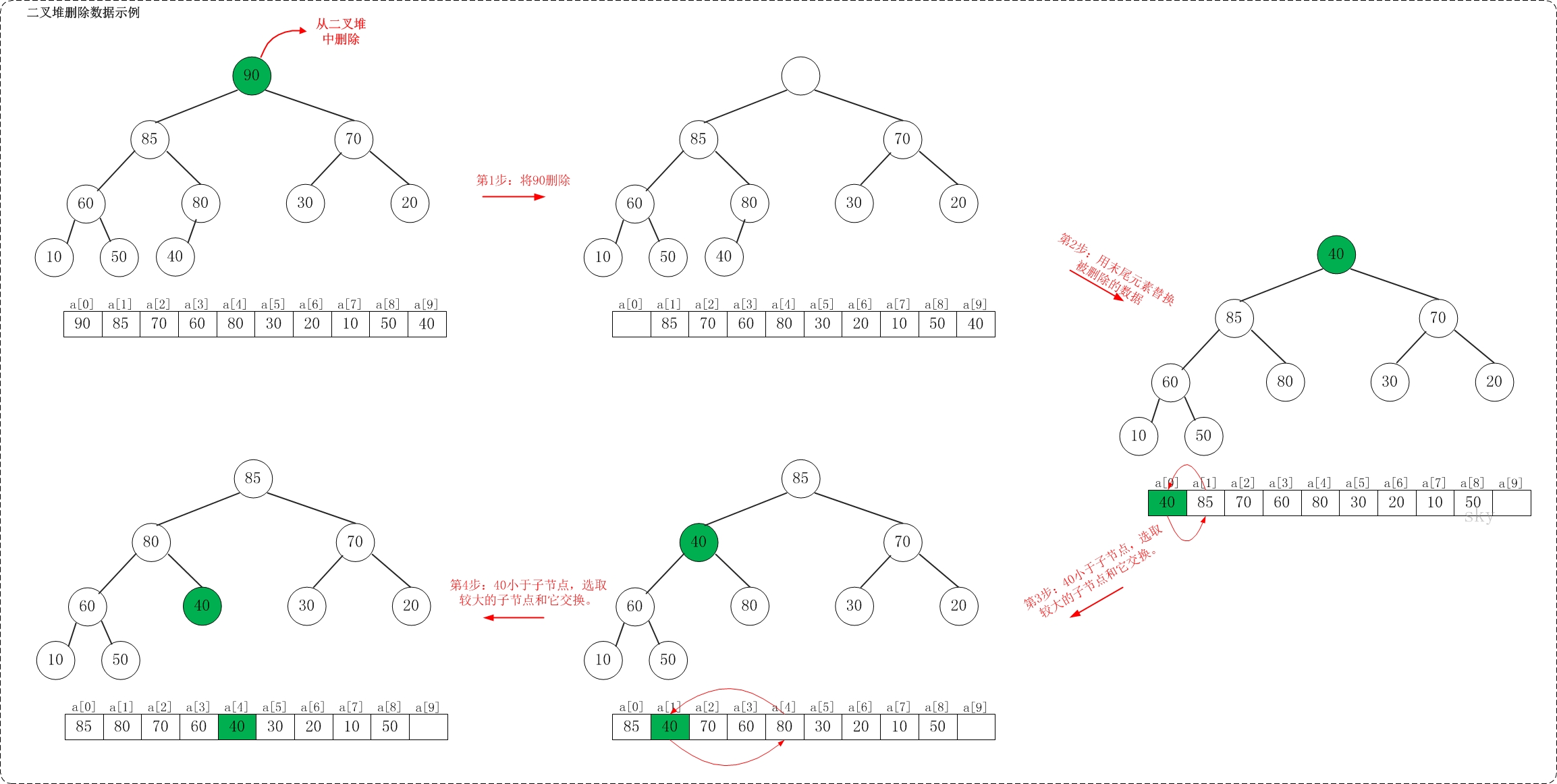
-
二叉堆我们一般只考虑对根结点的删除
-
当从最大堆中删除根结点时:
- 用数组中最后一个元素替换根结点,且元素个数减一
- 新根是否满足大根堆性质,如果不满足,和较大的子结点交换
- 对交换后子树依次判断,直到满足大根堆或到达最后一层。
-
代码实现
void Pop(){//向下调整 swap(Heap[siz],Heap[1]);siz--;//交换堆顶和堆底,然后直接弹掉堆底 for(int i=1;2*i<=siz;i*=2){ int j=2*i;//如果存在右儿子且右儿子大于左儿子j就指向右儿子 if(j+1<=siz && Heap[j]<Heap[j+1])++j; if(Heap[i]<Heap[j])swap(Heap[i],Heap[j]); else break; } }
-
10.6.5 堆排序
-
堆排序 (
Heapsort) 是指利用堆这种数据结构所设计的一种排序算法。 -
堆是一个近似完全二叉树的结构,并同时满足堆的性质:即子结点的键值或索引总是小于(或者大于)它的父结点。
-
堆排序可以说是一种利用堆的概念来排序的选择排序。分为两种方法:
- 大顶堆:每个结点的值都大于或等于其子结点的值,在堆排序算法中用于升序排列;
- 小顶堆:每个结点的值都小于或等于其子结点的值,在堆排序算法中用于降序排列;
-
堆排序的平均时间复杂度为
Ο(nlogn)。 -
算法步骤:
- 创建一个堆
- 把堆首(最大值)和堆尾互换;
- 堆的大小减一,并向下调整堆使之满足堆的性质
- 重复
2,3直到只剩一个元素。
-
代码实现:
#include <cstdio> #include <cstring> const int maxn = 10000 + 5; void swap(int &x,int &y){int t=x;x=y;y=t;}//交换函数 int Heap[maxn],siz=0; void Push(int x){//向上调整 Heap[++siz]=x;//把插入的元素x放在数组最后 for(int i=siz;i/2>0 && Heap[i]>Heap[i/2];i=i/2) swap(Heap[i],Heap[i/2]); } void Pop(){//向下调整 swap(Heap[siz],Heap[1]);siz--;//交换堆顶和堆底,然后直接弹掉堆底 for(int i=1;2*i<=siz;i*=2){ int j=2*i;//如果存在右儿子且右儿子大于左儿子j就指向右儿子 if(j+1<=siz && Heap[j]<Heap[j+1])++j; if(Heap[i]<Heap[j])swap(Heap[i],Heap[j]); else break; } } void Solve(){ int n;scanf("%d",&n); for(int i=1;i<=n;++i){//建堆 int x;scanf("%d",&x); Push(x); } for(int i=1;i<=n;++i){//输出堆顶并删除,此乃降序 printf("%d ",Heap[1]);Pop(); } printf("\n"); for(int i=1;i<=n;++i)//全部出堆后原数组为升序 printf("%d ",Heap[i]); } int main(){ Solve(); return 0; }
10.7 Trie 树
10.7.1 Trie字典树的基本概念
-
在计算机科学中,Trie,又称前缀树或字典树,是一种有序树,用于保存关联数组,其中的键通常是字符串。
-
与二叉查找树不同,键不是直接保存在结点中,而是由结点在树中的位置决定。
-
一个结点的所有子孙都有相同的前缀,也就是这个结点对应的字符串,而根结点对应空字符串。
-
一般情况下,不是所有的结点都有对应的值,只有叶子结点和部分内部结点所对应的键才有相关的值
-
Trie 字典树(主要用于存储字符串)查找速度主要和它的元素(字符串)的长度相关。
-
也就是说如果只考虑小写的 26 个字母,那么 Trie 字典树的每个结点都可能有 26 个子结点。
-
例如我们往字典树中插入
see、pain、paint三个单词,Trie 字典树如下所示: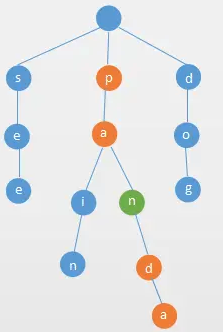
-
10.7.2 Trie字典树的基本操作
- 我们通过动态申请内存的形式来实现
Trie树的结构。 - 单词字符串的每个字符作为一个
Node结点,Node主要有两部分组成:- 从根到该结点是否是一个单词 (
bool isWord) - 结点所有的子结点,用固定长度的指针数组来表示
- 从根到该结点是否是一个单词 (
struct Node {
bool isWord;//为1表示从根到当前结点是一个单词
Node *son[N];//const int N=26;
Node(){
isWord = false;
memset(son, 0, sizeof(son));
}
};
-
插入
- 对带插入的单词从首字母开始,从树根往下查找,如果当前字母已存在,依次从下一层找下一个字母。
- 如果
Trie树上当前结点不存在单词所要查找的字母,直接新建一个结点挂上去,依次新建其他结点直到单词结束; - 如果插入的单词是已插入单词的前缀,只需查找到当前单词的末尾添上单词标记,即
isWord=1.
-
示例代码
void insert(Node *root,char str[]) { // 插入一个单词 int len = strlen(str), id; Node *now = root; for (int i = 0; i < len; ++i) {//遍历单词 id = str[i] - 'A';//大写字母映射到0~25 if (now->son[id] == NULL) {//当前结点不存在新建新的结点 now->son[id] = new Node; ++cnt; // 用来记录总结点个数 } now = now->son[id];//下调一层,准备下一个字母 } now->isWord = true; // 标记从根到此为一个单词 }
-
查找
-
Trie 查找操作就比较简单了,遍历待查找的字符串的每个字符:
- 如果某个结点不存在,则查找失败;
- 如果每个对应的结点都存在,并且待查找字符串的最后一个字符对应的
Node的isWord属性为true,则表示该单词存在。
-
-
示例代码
bool findword(Node *root,char str[]) { // 查找一个单词是否存在 int len = strlen(str), id; Node *now = root;//从根结点开始 for (int i = 0; i < len; ++i) {//遍历单词 id = str[i] - 'A'; if (now->son[id] == NULL) return false; //对应的孩子不存在,查找失败 now = now->son[id];//下调一层 } return now->isWord; }
-
前缀查询
-
如果需要查找是否存在某个前缀字符串
s,用 Trie 树也比较方便。前缀查询和上面的查询操作基本类似,就是不需要判断isWord了 -
示例代码
bool findprefix(Node *char str[]) { // 查找是否存在某个前缀 int len = strlen(str), id; Node *now = root; for (int i = 0; i < len; ++i) { id = str[i] - 'A'; if (now->son[id] == NULL) return false; now = now->son[id]; } return true;//只要能找到每一个字母就是前缀 }
-
-
升序排列
-
如果想要把所有的字符串升序排列再输出,同样可以实现,只需要从左到右沿着每条链从根结点走到所有的
isWord被标记为true的结点,并把中间经过的结点对应的字符依次输出即可。 -
由于可能存在几个单词在同一条链上的情况,为了则前缀是共有的,所以我们可以借助数组来保存递归时找到的公共的前缀字符串。
-
示例代码
// 直接调用该函数即可,由于有可能几个单词都在一条链上,所以借助一个 void strsort(Node *now) { // 将单词升序输出 vector<char> v; walk(now, v); } void walk(Node *now, vector<char> &v) { // 递归遍历,给strsort调用的 if (now == NULL) return; if (now->isWord) print(v); // 找到了一个单词,直接输出 for (int i = 0; i < MAX_CHILD; ++i) {// 回溯法遍历每个结点的所有孩子, if (now->son[i] != NULL) { v.push_back('A'+i); walk(now->son[i], v); v.pop_back(); // 某条分支走完回来后,修改当前字符,换一条分支继续走 } } } void print(vector<char> &v) { // 负责输出单词的函数 int s = v.size(); for (int i = 0; i < s; ++i) { printf("%c", v[i]); } putchar('\n'); }
-
-
删除
Trie树的删除使用很少,而且稍微复杂一些,主要分为以下3种情况:
-
单词是另一个单词的前缀
- 如果待删除的单词是另一个单词的前缀,只需要把该单词的最后一个结点的
isWord的改成false。 - 比如 Trie 中存在
panda和pan这两个单词,删除pan,只需要把字符n对应的结点的isWord改成false即可。- 如下图所示

- 如果待删除的单词是另一个单词的前缀,只需要把该单词的最后一个结点的
-
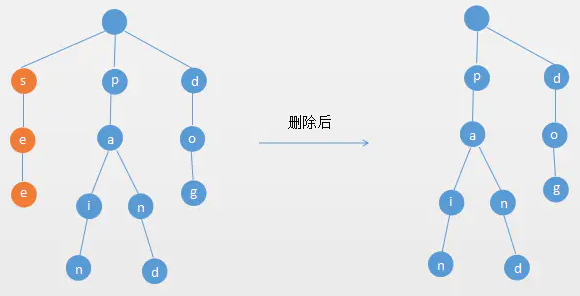
单词的所有字母的都没有多个分支,删除整个单词
- 如果单词的所有字母的都没有多个分支(也就是说该单词所有的字符对应的
Node都只有一个子结点),则删除整个单词。 - 例如要删除如下图的
see单词,如下图所示:
- 如果单词的所有字母的都没有多个分支(也就是说该单词所有的字符对应的
- 如果单词的除了最后一个字母,其他的字母有多个分支
- 这种情况,需要找到最下面的分支结点,将以下的单词部分删掉,如下图所示:
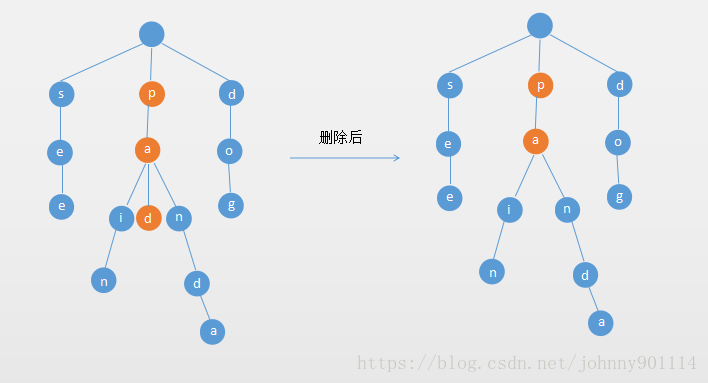
- 这种情况,需要找到最下面的分支结点,将以下的单词部分删掉,如下图所示:




