LCA

LCA简介:

给定一棵树,求两点的最近公共祖先.

参考例题蓝桥杯第十三届B组c++ I题景区导游

https://www.dotcpp.com/oj/problemset.php?search=%E8%93%9D%E6%A1%A5%E6%9D%AF2023

可以用两种方法求解LCA问题:

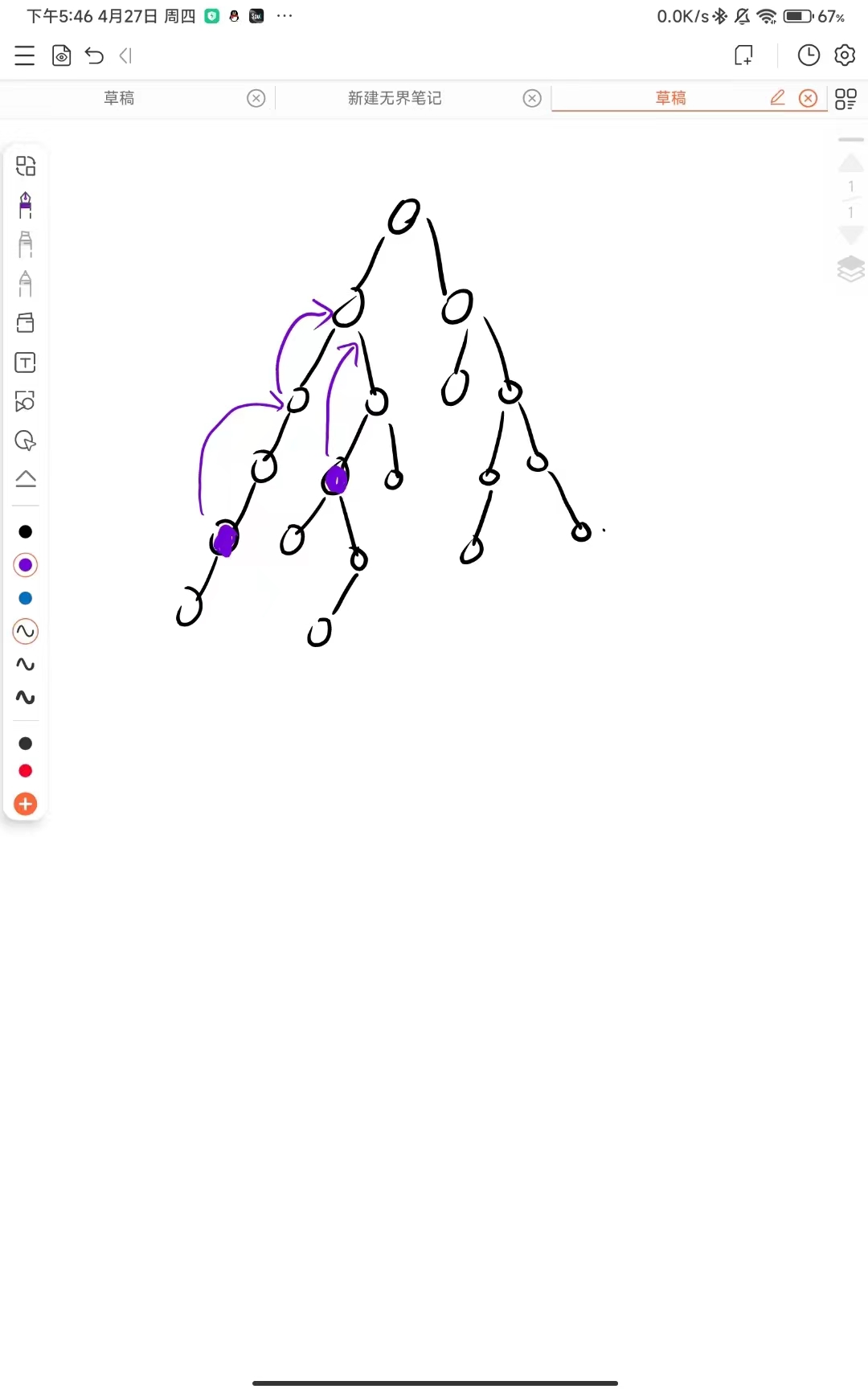
树上倍增法:

通过记录当前点的2的幂次级父节点,来进行跳跃上升找祖先.设祖先为F,当前节点为u,祖先和当前节点的深度差为dep,dep可分为多个2的幂次二项式之和,所以只要通过多次跳跃即可找到祖先,这样比一级一级跳会快很多.

题解:

#include<bits/stdc++.h>
using namespace std;
#define ull unsigned long long
#define int long long
#define endl "\n"
#define debug freopen("C:/Users/HBH/Desktop/1.txt","w",stdout);
int fa[100005][30];
unordered_map<int, int>len[100005];
int dep[100005];
vector<pair<int, int>>d[100005];
unordered_map<int, int>m[100005];
void dfs(int now, int f)
{
    len[now][now] = 0;
    dep[now] = dep[f] + 1;
    fa[now][0] = f;
    len[now][f] = m[now][f];
    for (int i = 1; (1 << i) <= dep[now]; i++)
    {
        fa[now][i] = fa[fa[now][i - 1]][i - 1];
        len[now][fa[now][i]] = len[fa[now][i - 1]][fa[fa[now][i - 1]][i - 1]] + len[now][fa[now][i - 1]];
    }
    for (int i = 0; i < d[now].size(); i++)
    {
        if (d[now][i].first != f)
            dfs(d[now][i].first, now);
    }
}
int lca(int u, int v)
{
    int sum = 0;
    if (dep[u] > dep[v])
    {
        swap(u, v);
    }
    for (int i = 20; i >= 0 ; i--)
    {
        if (dep[fa[v][i]] >= dep[u]) { sum += len[v][fa[v][i]]; v = fa[v][i];}
        if (u == v)return sum;
    }
    for (int i = 20; i >= 0; i--)
    {
        if (fa[u][i] != fa[v][i])
        {
            sum += len[v][fa[v][i]];
            sum += len[u][fa[u][i]];
            v = fa[v][i];
            u = fa[u][i];
        }
    }
    return sum + len[u][fa[u][0]] + len[v][fa[v][0]];
}
signed main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    int n, k;
    cin >> n >> k;
    int root;
    for (int i = 0; i < n - 1; i++)
    {
        int u, v, t;
        cin >> u >> v >> t;
        root = u;
        d[u].push_back({v, t});
        d[v].push_back({u, t});
        m[u][v] = t;
        m[v][u] = t;
    }
    dfs(root, 0);
    vector<int>a;
    for (int i = 0; i < k; i++)
    {
        int t;
        cin >> t;
        a.push_back(t);
    }
    int sum = 0;
    for (int i = 1; i < k; i ++) sum += lca(a[i - 1], a[i]);
    for (int i = 0; i < k; i ++) {
        int ans = sum;
        if (i != 0) ans -= lca(a[i], a[i - 1]);
        if (i != k - 1) ans -= lca(a[i], a[i + 1]);
        if (i != 0 && i != k - 1) ans += lca(a[i - 1], a[i + 1]);
        cout << ans << " ";
    }
}

树上倍增板子:

#include<bits/stdc++.h>
using namespace std;
#define ull unsigned long long
#define int long long
#define endl "\n"
#define debug freopen("C:/Users/HBH/Desktop/1.txt","w",stdout);
int fa[100005][30];int dep[100005];
vector<pair<int, int>>d[100005];void dfs(int now, int f)
{
    dep[now] = dep[f] + 1;
    fa[now][0] = f;//2的0次就是当前父亲for (int i = 1; (1 << i) <= dep[now]; i++)//类似dp思路
    {
        fa[now][i] = fa[fa[now][i - 1]][i - 1];
    }
    for (int i = 0; i < d[now].size(); i++)
    {
        if (d[now][i].first != f)
            dfs(d[now][i].first, now);
    }
}
int lca(int u, int v)
{
    int sum = 0;
    if (dep[u] > dep[v])
    {
        swap(u, v);
    }
    for (int i = 20; i >= 0 ; i--)//使u和v的深度一样
    {
        if (dep[fa[v][i]] >= dep[u]) { v = fa[v][i];}
        if (u == v)return u;
    }
    for (int i = 20; i >= 0; i--)
    {
        if (fa[u][i] != fa[v][i])//同时上升
        {
            v = fa[v][i];
            u = fa[u][i];
        }
    }
    return fa[u][0];
}
signed main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    int n, k;
    cin >> n >> k;
    int root;
    for (int i = 0; i < n - 1; i++)
    {
        int u, v, t;
        cin >> u >> v >> t;
        root = u;
        d[u].push_back({v, t});
        d[v].push_back({u, t});
        m[u][v] = t;
        m[v][u] = t;
    }
    dfs(root, 0);
    
}

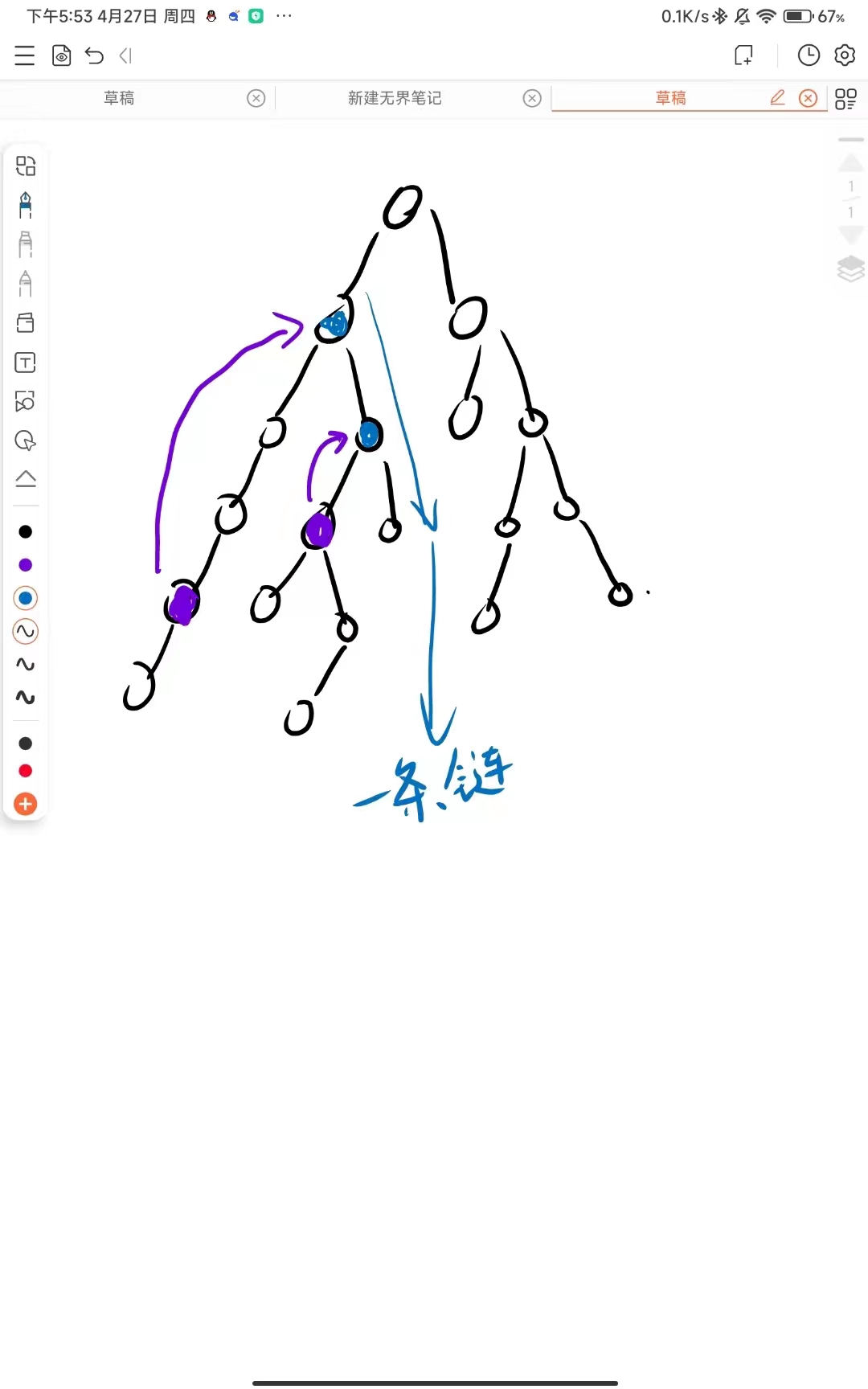
树链剖分法求LCA(最快):

首先预处理每个子树的大小和每个节点的深度，并对每个点选择子树大小最大的儿字作为重儿子，然后顺着重儿子dfs，把重链顶点标记到每个点上。
接着求LCA时，就从两个点选dep[top[x]]更大的，跳到fa[top[x]],直到两个节点都在同一条重链上（即top[x]相等）
这样我们就在O(n）预处理的情况下，O(log n）地在线回答了LCA问题，并且常数因子非常小，比倍增的要小得多.
也就是标记每个子链,当两点处于一条链时即可直接找到祖先.

 

 题解

#include<bits/stdc++.h>
using namespace std;
#define ull unsigned long long
#define int long long
#define endl "\n"
#define debug freopen("C:/Users/HBH/Desktop/1.txt","w",stdout);
int fa[100005];
int len[100005];
int dep[100005];
int size[100005];
int son[100005];
int top[100005];
vector<pair<int, int>>d[100005];
unordered_map<int, int>m[100005];
void dfs1(int now, int f)
{
    dep[now] = dep[f] + 1;
    size[now]=1;
    fa[now] = f;
    len[now] = m[now][f]+len[fa[now]];//通过递归计算从根到该点的距离
    for (int i = 0; i < d[now].size(); i++)
    {
        if(d[now][i].first==f)continue;
        fa[d[now][i].first]=now;
        dfs1(d[now][i].first, now);
        size[now]+=size[d[now][i].first];
        if(size[d[now][i].first]>size[son[now]])son[now]=d[now][i].first;
    }
}
void dfs2(int now,int topp)
{
    top[now]=topp;
    if(son[now])dfs2(son[now],topp);
    for (int i = 0; i < d[now].size(); i++)
    {
        if(d[now][i].first==fa[now]||d[now][i].first==son[now])continue;
        dfs2(d[now][i].first,d[now][i].first);
    }
}
int lca(int u, int v)
{
    while(top[u]!=top[v])
    {
        if(dep[top[u]]<dep[top[v]])swap(u,v);
        u=fa[top[u]];
    }
    return dep[u]<dep[v]?u:v;
}
int getlca(int u,int v)
{
    return len[u]+len[v]-2*len[lca(u,v)];//计算距离
}
signed main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    int n, k;
    cin >> n >> k;
    int root;
    for (int i = 0; i < n - 1; i++)
    {
        int u, v, t;
        cin >> u >> v >> t;
        root = u;
        d[u].push_back({v, t});
        d[v].push_back({u, t});
        m[u][v] = t;
        m[v][u] = t;
    }
    dfs1(root, 0);
    dfs2(root,root);
    vector<int>a;
    for (int i = 0; i < k; i++)
    {
        int t;
        cin >> t;
        a.push_back(t);
    }
    int sum = 0;
    for (int i = 1; i < k; i ++) sum += getlca(a[i - 1], a[i]);
    for (int i = 0; i < k; i ++) {
        int ans = sum;
        if (i != 0) ans -= getlca(a[i], a[i - 1]);
        if (i != k - 1) ans -= getlca(a[i], a[i + 1]);
        if (i != 0 && i != k - 1) ans += getlca(a[i - 1], a[i + 1]);
        cout << ans << " ";
    }
}

 

显然树链剖分快好多倍

树链剖分板子:

#include<bits/stdc++.h>
using namespace std;
#define ull unsigned long long
#define int long long
#define endl "\n"
#define debug freopen("C:/Users/HBH/Desktop/1.txt","w",stdout);
int fa[100005];int dep[100005];
int size[100005];
int son[100005];
int top[100005];
vector<pair<int, int>>d[100005];
unordered_map<int, int>m[100005];
void dfs1(int now, int f)
{
    dep[now] = dep[f] + 1;
    size[now]=1;
    fa[now] = f;
    for (int i = 0; i < d[now].size(); i++)
    {
        if(d[now][i].first==f)continue;
        fa[d[now][i].first]=now;
        dfs1(d[now][i].first, now);
        size[now]+=size[d[now][i].first];
        if(size[d[now][i].first]>size[son[now]])son[now]=d[now][i].first;
    }
}
void dfs2(int now,int topp)
{
    top[now]=topp;
    if(son[now])dfs2(son[now],topp);
    for (int i = 0; i < d[now].size(); i++)
    {
        if(d[now][i].first==fa[now]||d[now][i].first==son[now])continue;
        dfs2(d[now][i].first,d[now][i].first);
    }
}
int lca(int u, int v)
{
    while(top[u]!=top[v])//往上找直到找到两个点在同一链
    {
        if(dep[top[u]]<dep[top[v]])swap(u,v);
        u=fa[top[u]];
    }
    return dep[u]<dep[v]?u:v;
}

signed main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    int n, k;
    cin >> n >> k;
    int root;
    for (int i = 0; i < n - 1; i++)
    {
        int u, v, t;
        cin >> u >> v >> t;
        root = u;
        d[u].push_back({v, t});
        d[v].push_back({u, t});
        m[u][v] = t;
        m[v][u] = t;
    }
    dfs1(root, 0);
    dfs2(root,root);

}