honoka和格点三角形

题目：

honoka最近在研究三角形计数问题。
她认为，满足以下三个条件的三角形是“好三角形”。
1.三角形的三个顶点均为格点，即横坐标和纵坐标均为整数。
2.三角形的面积为 。
3.三角形至少有一条边和 轴或 轴平行。
honoka想知道，在平面中选取一个大小为  的矩形格点阵，可以找到多少个不同的“好三角形”？由于答案可能过大，请对 取模。

 

思路：
分两种情况讨论：

（1）两条边和两个坐标轴平行

（2）只有一条边和某个坐标轴平行

首先根据题中的条件可以看出三角型是低与高是1*2或是2*1.
第一种情况：

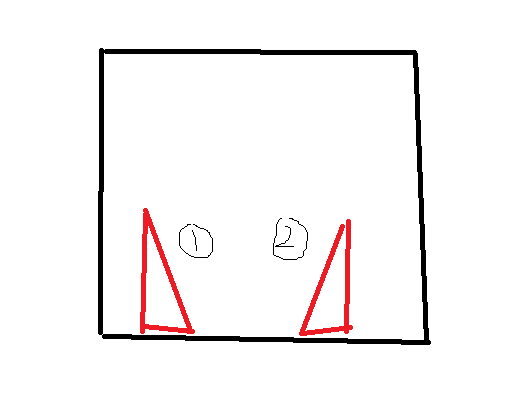
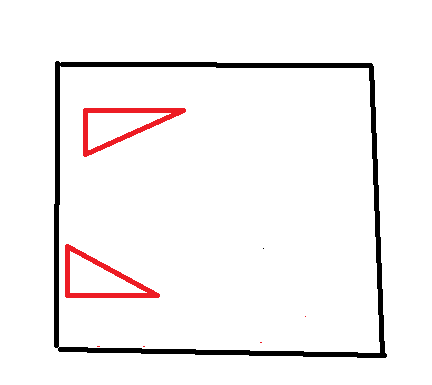
如图，一共有4*(n-2)*(m-1)+4*(m-2)*(n-1)种。

第二种情况：

可以分为底边为 2、高为 1 和底边为 1 、高为 2的情况。
①对于底边为2，高为1

 

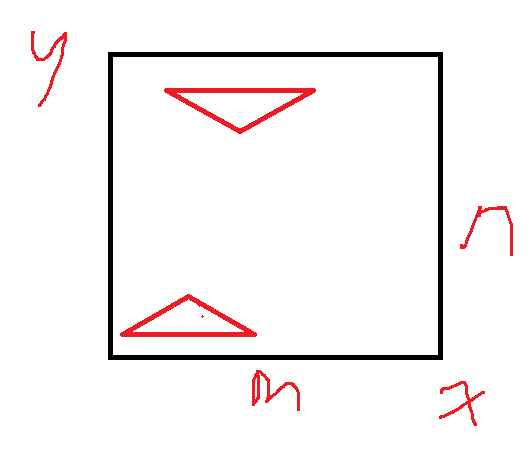
若底边和x轴平行，那么底边在x方向上有 m−2 种可能，顶点在x方向上也有 m−2(顶点的位置一共有m个，减去第一种情况中的两种)种可能，在y方向上有 n-1 种可能；

故共有2*（m-2)*(m-2)*(n-1)

若底边和y轴平行，同理可推出2*（n-2)*(n-2)*(m-1)

②对于底边为1，高为2的情况

 

底边与x轴平行时 2*(m-1)*(m-2)*(n-2)

底边与y轴平行时2*(n-1)*(n-2)*(m-2)。

最后将所有的情况的都加起来最终解，注意用long long 存储，进行相加的时候要及时取模。

代码：

#include <map>
#include <set>
#include <list>
#include <stack>
#include <queue>
#include <deque>
#include <cmath>
#include <ctime>
#include <string>
#include <limits>
#include <cstdio>
#include <vector>
#include <iomanip>
#include <cstdlib>
#include <cstring>
#include <istream>
#include <iostream>
#include <algorithm>
#define ci cin
#define co cout
#define el endl
#define Scc(c) scanf("%c",&c)
#define Scs(s) scanf("%s",s)
#define Sci(x) scanf("%d",&x)
#define Sci2(x, y) scanf("%d%d",&x,&y)
#define Sci3(x, y, z) scanf("%d%d%d",&x,&y,&z)
#define Scl(x) scanf("%I64d",&x)
#define Scl2(x, y) scanf("%I64d%I64d",&x,&y)
#define Scl3(x, y, z) scanf("%I64d%I64d%I64d",&x,&y,&z)
#define Pri(x) printf("%d\n",x)
#define Prl(x) printf("%I64d\n",x)
#define Prc(c) printf("%c\n",c)
#define Prs(s) printf("%s\n",s)
#define For(i,x,y) for(int i=x;i<y;i++)
#define For_(i,x,y) for(int i=x;i<=y;i++)
#define FFor(i,x,y) for(int i=x;i>y;i--)
#define FFor_(i,x,y) for(int i=x;i>=y;i--)
#define Mem(f, x) memset(f,x,sizeof(f))
#define LL long long
#define ULL unsigned long long
#define MAXSIZE 100005
#define INF 0x3f3f3f3f

const int mod=1e9+7;
const double PI = acos(-1.0);

using namespace std;

int main(){
    LL n,m;
    //Sci2(n,m);
    ci>>n>>m;
    LL sum=(n-2)*(m-1)*4%mod+(n-1)*(m-2)*4%mod;
    sum=(sum+2*(n-1)*(m-2)%mod*(m-2)%mod+2*(m-1)*(n-2)%mod*(n-2)%mod)%mod;
    sum=(sum+2*(n-2)*(m-1)%mod*(m-2)%mod+2*(m-2)*(n-1)%mod*(n-2)%mod)%mod;
    co<<sum;
    return 0;
}