第24章 PWM DAC介绍

第二十四章 PWM DAC介绍

1. 导入

上一章，我们介绍了 STM32F4 自带 DAC 模块的使用，但有时候，可能两个 DAC 不够用，此时，我们可以通过 PWM+RC 滤波来实一个 PWM DAC。本章我们将向大家介绍如何使用 STM32F4 的 PWM 来设计一个 DAC。我们将使用按键（或 USMART）控制 STM32F4的 PWM 输出，从而控制 PWM DAC 的输出电压，通过 ADC1 的通道 5 采集 PWM DAC 的输出电压，并在 LCD 模块上面显示 ADC 获取到的电压值以及 PWM DAC 的设定输出电压值等信息。

2. PWM DAC 简介

有时候， STM32F4 自带的 2 路 DAC 可能不够用，需要多路 DAC，外扩 DAC 成本又会高不少。此时，我们可以利用 STM32F4 的 PWM+简单的 RC 滤波来实现 DAC 输出，从而节省成本。 在精度要求不是很高的时候， PWM+RC 滤波的 DAC 输出方式，是一种非常廉价的解决方案。

PWM 本质上其实就是是一种周期一定，而高低电平占空比可调的方波。实际电路的典型 PWM 波形，如图所示：

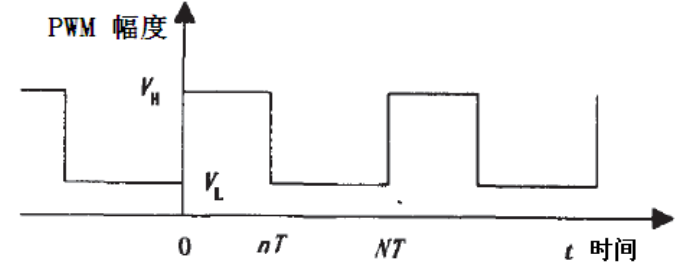
图的 PWM 波形可以用分段函数表示为式①：

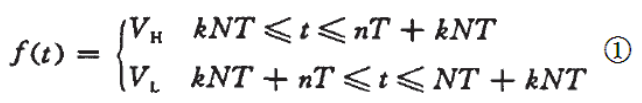
其中： T 是单片机中计数脉冲的基本周期，也就是 STM32F4 定时器的计数频率的倒数。N 是 PWM 波一个周期的计数脉冲个数，也就是 STM32F4 的 ARR-1 的值。 n 是 PWM 波一个周期中高电平的计数脉冲个数，也就是 STM32F4 的 CCRx 的值。 VH 和 VL 分别是 PWM波的高低电平电压值， k 为谐波次数， t 为时间。我们将①式展开成傅里叶级数，得到公式②：

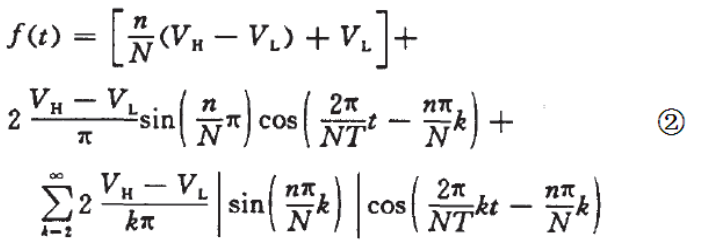
从②式可以看出，式中第 1 个方括弧为直流分量，第 2 项为 1 次谐波分量，第 3 项为大于 1 次的高次谐波分量。式②中的直流分量与 n 成线性关系，并随着 n 从 0 到 N，直流分量从 VL 到 VL+VH 之间变化。这正是电压输出的 DAC 所需要的。因此， 如果能把式②中除直流分量外的谐波过滤掉，则可以得到从 PWM 波到电压输出 DAC 的转换，即： PWM 波可以通过一个低通滤波器进行解调。式②中的第 2 项的幅度和相角与 n 有关，频率为 1/ （NT），其实就是 PWM 的输出频率。该频率是设计低通滤波器的依据。如果能把 1 次谐波很好过滤掉，则高次谐波就应该基本不存在了。

通过上面的了解，我们可以得到 PWM DAC 的分辨率，计算公式如下：

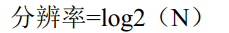
这里假设 n 的最小变化为 1，当 N=256 的时候，分辨率就是 8 位。而 STM32F4 的定时器大部分都是 16 位的（TIM2 和 TIM5 是 32 位），可以很容易得到更高的分辨率，分辨率越高，速度就越慢。不过我们在本章要设计的 DAC 分辨率为 8 位。

在 8 位分辨条件下，我们一般要求 1 次谐波对输出电压的影响不要超过 1 个位的精度，也就是 3.3/256=0.01289V。假设 VH 为 3.3V， VL 为 0V，那么一次谐波的最大值是 2*3.3/ π =2.1V，这就要求我们的 RC 滤波电路提供至少-20lg(2.1/0.01289)=-44dB 的衰减。

STM32F4 的定时器最快的计数频率是 168Mhz，某些定时器只能到 84M，所以我们以84M 频率为例介绍， 8 为分辨率的时候， PWM 频率为 84M/256=328.125Khz。如果是 1 阶RC 滤波，则要求截止频率 2.07Khz，如果为 2 阶 RC 滤波，则要求截止频率为 26.14Khz。

探索者 STM32F4 开发板的 PWM DAC 输出采用二阶 RC 滤波，该部分原理图如图：

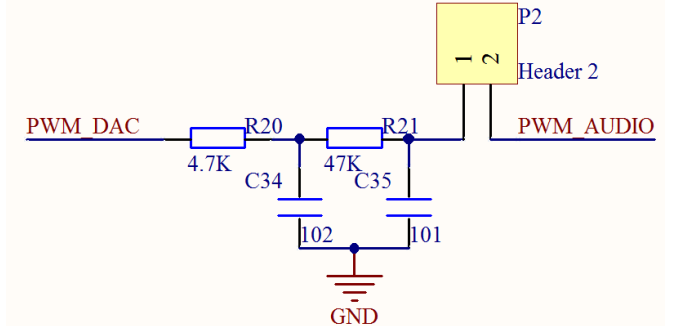
二阶 RC 滤波截止频率计算公式为：

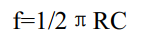
以上公式要求 R28C37=R29C38=RC。根据这个公式，我们计算出图的截止频率为： 33.8Khz 超过了 26.14Khz，这个和我们前面提到的要求有点出入，原因是该电路我们还需要用作 PWM DAC 音频输出，而音频信号带宽是 22.05Khz，为了让音频信号能够通过该低通滤波，同时为了标准化参数选取，所以确定了这样的参数。实测精度在 0.5LSB 左右。