CFA知识点:久期为什么难理解
CFA知识点:久期为什么难理解
CFA的固定收益(Fixed Income)科目中,久期(Duration)是一个核心概念,也是固收实务中的重要概念。但是这个名字就让人看不懂什么意思,而实际上久期的涉及的名词定义众多,理解角度多,应用场景也多,常常让人傻傻分不清楚。久期到底是什么?怎么区分不同的久期概念?本文尝试在这两个问题上做些尝试。
为什么要提出久期?
投资一个标的(股票、债券等等),核心就是要衡量两个要素:收益和风险(Return & Risk)。所以围绕这两个要素,我们分别理解两个最重要的久期概念。
Macaulay Duration 麦考利久期
首先,第一个被提出的久期概念:Macaulay Duration 麦考利久期,它的提出是为了解决一个非常直接的问题:怎么比较两个价格(现值)一样的债券的风险?
例如,假设有两个现值一样的债券,都还有5年到期,债券A要到5年底才一次性偿还所有钱,债券B每年年底都会偿还一部分。这样看是不是觉得债券B实际的偿还期要比债券A短?偿还期越短,不确定性就越低,风险就越小,所以为了衡量一个债券的实际还款期一个神奇的概念诞生了:
麦考利久期:以现金流现值为权重的平均还款期。权重等于某一现金流现值除以价格(也就是所有现金流的现值)。
Macaulay Duration is the weighted average term to maturity of the cash flows. The weight of each cash flow is determined by dividing the present value of the cash flow by the price(the total present value of all cash flows)
我们拆开来看,理解Macaulay Duration有两个关键点:
- 平均还款期:一种时间概念,单位是时间
- 以现金流现值为权重
从这个定义,我们可以直接推出它的计算公式:
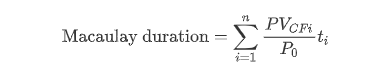
其中:
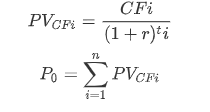
也就是说,Macaulay Duration本质上是从时间的角度(实际还款期)来看不同债券的风险,它并没有直接与收益率建立关系。
为了充分理解Macaulay Duration,我们还要再谈两点:
-
对于零息债券,Macaulay Duration = Maturity(到期期限),因为 P = PV(CF1)。例如5年期零息债,Mac D就是板上钉钉的5年(和收益率变动无关)。换个角度说,5年付息债券的Mac D一定小于5年,所以Maturity一样的情况下Coupon bearing bond 的Mac D < Zero Coupon Bond的Mac D。
-
Mac D是持有债券的Price risk 和 Reinvestment risk相互抵消的平衡点。
-
Price risk (价格风险) is the uncertainty of proceeds if a bond must be sold before maturity. 假设债券持有到期,到期价格=par,这样价格风险是最低的,但是如果在到期前卖出,卖出越早(持有期越短),价格不确定性越高。
-
Reinvestment risk(再投资风险) is the uncertain FV of any cash flows received and reinvested
before the end of the holding period. 对于付息债券,收到利息后,为了维持整体收益率,还需要将利息再投资到收益率与债券一致的产品中,但是市场中可能很难找到收益率一致的产品,所以再投资也是有风险的,而且持有期限越长,收到的利息越多,再投资的时间越长,风险越大。 -
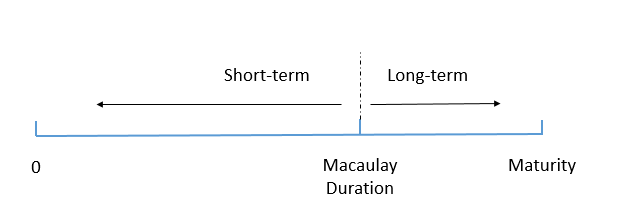
这样一方面,持有期从0到T,价格风险越来越低,再投资风险越来越高,那么如果持有期=Mac D时,价格风险=再投资风险。再由此,在CFA有个默认的认识:
- 如果Holding period >Mac D则说明,主要风险和收益来自再投资活动,属于长期投资导向;
- 如果Holding period >Mac D,则主要风险和收益来自短期价格变动,属于短期投资导向。
-
Modified Duration 修正久期
Modified Duration 修正久期,虽然与都叫久期,但是与Macaulay Duration的理解角度完全不同,Mod D是为了量化的回答:当债券收益率yield 变化1%时债券价格P会变化多少个百分点的问题。为什么这个问题很重要?让我们再回到投资标的最重要的两点:收益和风险 来讨论。
收益和风险怎么算?让我们从最简单的例子开始看。
假设一个投资标的在持有期间没有产生现金流,那么从投资的结果来看,投资收益率取决于价格变动:
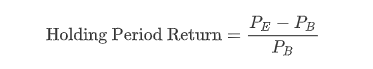
对应的,我们从最简化的债券开始:对于以一个零息国债,假设持有期间收益率y不变,那么债券投资收益率与上面的公式相同。P-B在买入时就已经确定的,所以决定收益率变量是P-E,那么P-E取决于什么,最常用的P-E定价公式,就是折现公式,对于零息债券:
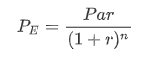
在这个公式里,假设持有到期,Par和n都是在买入时就确定的,唯一不确定的就是折现率r,因为是会随时间变化而变化的。也就是说决定P-E的关键因素在于r。而对于零息国债,r = 债券预期收益率y
进而有了这样的一个逻辑:债券投资收益率R <= P-E <= 债券预期收益率y
那么如何考察P-E和y的关系,这时Modified Duration的概念就被引入了,Mod D = 当债券收益率yield 变化1%时债券价格P会变化多少个百分点。
从定义角度看:
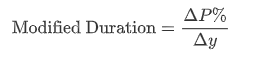
而实务操作中,一般Mod Dur都是市场机构或软件告知的,我们一般会这样运用:

总的来说,Modified Duration本质上从价格与折现率(预期收益率)的相关性角度来衡量债券的风险,无风险债券的折现率可以看做无风险利率,因此Mod D与利率是直接相关的。
从本质上看,两者同样是衡量债券的风险,但是角度不同。Macaulay D和时间概念紧密相关的,但Modified D并不是。那为什么Modified D也同属Duration这个听起来像时间的概念呢?我觉得是因为两者在计算上是紧密相关的:
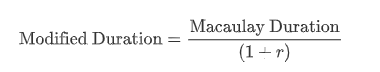
所以Mod D借鉴了Mac D的定义,但却并不是一个强时间属性的概念,它更偏向于敏感度或者风险属性。
计算上的关系和金融上的意义要区分理解,这是学习金融公式的一个特点,因为每个符号都代表了一个实务上不同的概念。
所以当我们谈论久期的时候,我们要依据场景弄清楚谈论的是Mac D还是Mod D,如果只是笼统定性的谈久期而不纠结细节,那么从Mod D和Mac D数量上紧密相关的关系看(两者同方向变化),我们可以将其归为一个本质(更偏向于Mod D的定义),其衡量的是债券的利率风险。
为了充分理解Modified Duration,我们还要补充几点:
-
依据定义公式上看,Mod D可以理解为价格P和预期收益率yield关系的一阶导数,也就是P-y图上的斜率
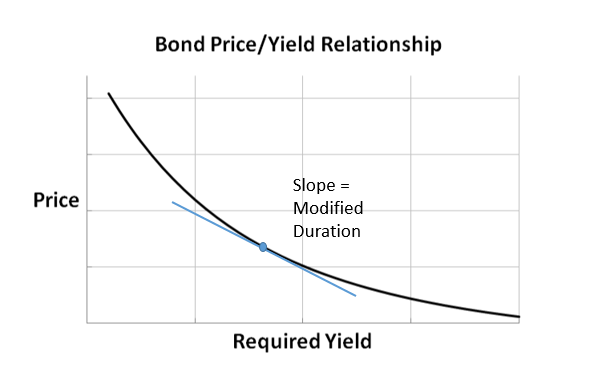
-
从上图可以看出来,P-y图上的每个点都代表的是y不同的债券,不同的点斜率不同,也就是Mod Duration不同。而这些不同的债券为什么y不同,这就要看另外一张图:Yield与Term to Maturity的关系。
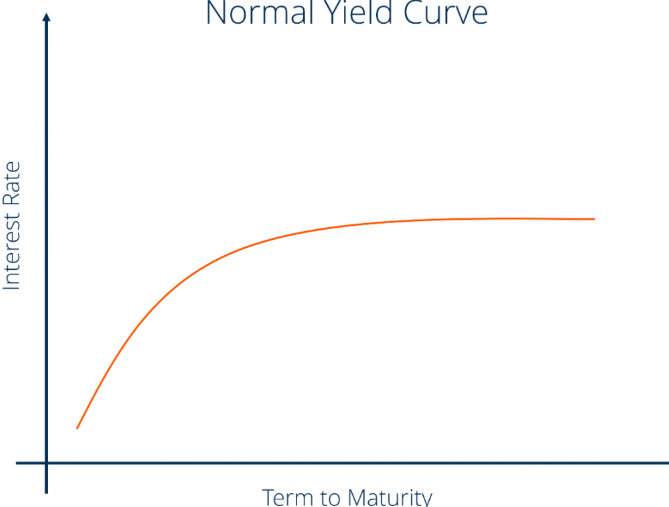
-
P-y图中,我们还可以看出,随着y的变化,斜率Mod D也在变化,这层关系是由Convexity来衡量的。
-
Mod Duration是会随着时间T的变化而变化的。这一点也可以从Mod Dur和Mac Dur的数量关系上看出来,因为Mac Dur是强时间概念,与剩余到期时间紧密相关。那么Mod Dur在数量上会与剩余时间相关。
其他的久期概念:
在学习和实务过程中,我们还会遇到很多上述两者之外的久期概念,下面列举几个,根据定义我们可以发现,这些久期都是从Mod Dur的角度出发来衡量P与某种收益率y的关系的。
-
Dollar Duration or Money Duration (紧密相关的还有PVBP/BPV/DV01这些概念)
-
定性:预期收益率变动1%,债券价格变动多少绝对金额$?
-
定义公式:Dollar Dur = delta P / delta y
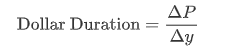
-
与Mod Dur的关系:Dollar Dur = Mod Dur * P
-
-
PVBP定义:预期收益率变动1 bp (= 0.01%),债券价格变动多少$? 与DD定义基本一致,只是数量上要 * 0.01
-
PVBP = Dollar Dur * 0.01
-
应用:

-
-
Effective Duration 有效久期(事后角度)
-
定义公式:
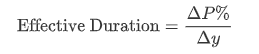
是不是看起来与Modified Duration一样?这时让我们来修正下之前的Mod Dur来突出两者的不同:
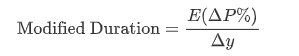
-
两者的不同在于
-
Effective Dur是基于事后的角度,用历史P数据来统计计算出某一历史期间内的delta P与 delta y关系,它更能反应基于历史的实际情况。
- Mod Dur是基于事前预期的角度,用预期P来计算出来的,它更能反应人们对未来的预期。
-
从这两个区别也可以初步了解为什么Effective Dur笔Mod Dur更适合衡量含权债券,因为含权债券的未来P很难预测(V bond = V pure bond + V option, Voption很难预测),因为预期P不靠谱所以基于历史的数据来衡量更合适。
-
-
Key Rate Duration (适用于Coupon bearing 债券)
- 定义:在term structure上不同M对应的债券的Modified Dur,这里的key rate一般指的市场上常见的2/3/5/10年期国债的yield。Key rate duration就是这些债券的久期,对应term structure上的几个key point, 通常我们简化认为,这些key rate的变动决定了整个term structure的变动。所以key rate duration是用来讨论债券预期收益率yield的term structure 非平行变动的常用工具。
- 因为我们可以把一个含息债券看做是几个零息债券的组合,简化为讨论多个不同M的零息债券与利率的关系。
-
Spread Duration (一般用于投资级公司债 Investment-graded corporate bond)
-
首先我们来看先公司债的收益率
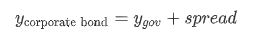
这里的spread也是收益率的一部分,一般是由信用风险导致的;
- 前面我们在讨论Mod Dur时都是假设为国债,也就是讨论 y gov(r f)与 P的关系。
- 而spread duration就是在讨论,假设y gov不变的情况下,spread变动(由公司信用风险变化导致)导致的P的变动%
-
定义公式:
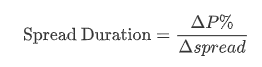
从本质上看,Spread Duration将公司债yield的Spread拆解出来,然后将Modified Duration的思想在Spread与P的关系上应用而已。其要考察的目的是衡量公司纯信用风险的部分对公司债价格的影响。
-
-
Portfolio Duration 投资组合久期
-
这个是个基于单个债券Mod Dur的数量计算概念,也就是一个投资组合里含有N个债券,对应不同的Mod Dur,那么计算这个Portfolio的Duration是多少?用于衡量组合整体的利率风险。
-
我们假设一个组合仅包含两个债券:债券1和债券2
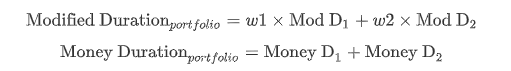
从含义上理解Money Duration为组合的价格金额变动 = 债券1的P金额变动 + 债券2的P金额变动。
-
总结
如果上面的概念一下子很难消化,那么请记住一点就够了,归根结底,久期最重要的两个概念是Macaulay duration和Modified duration,两个理解角度不同,当我们笼统定性谈久期时,更加偏向Modified duration的角度,本质是衡量债券价格与折现率的敏感程度,对于国债来说就是债券的利率风险。其余的duration概念多是Modified duration的衍生(与Macaulay duration 关系不大)
概念思维导图
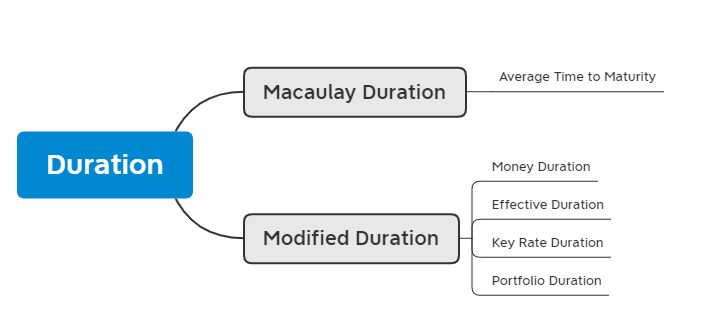
补充:
-
债券预期收益率完整构成公式:

参考链接:



