算法入门——红黑树(二)
算法入门——红黑树(二)
2020-09-01 11:40:35 hawk
概述
上一节中,我们分析了一下关于完美平衡的2-3查找树的各种操作,但仅仅是理论上的——换而言之,我们忽略了实现上的具体细节。这里我们将介绍一下基于红黑树(更具体的是左偏红黑树)的具有完美平衡性质的2-3查找树的具体代码实现,从而最终实现具有完美平衡的2-3查找树。
这里首先简单介绍一下红黑树——红黑树实际上是基于二叉查找树进行实现的,因为2-3查找树实际上也是有2-节点和3-节点构成的。因此红黑树通过在二叉查找树的节点中添加一些额外属性,从而抽象模拟2-节点和3-节点,进而模拟出2-3查找树。并且通过对于二叉查找树的简单修改,从而可以模拟出符合完美平衡性质的2-3查找树。
因此,本节我们将基于二叉查树的结构,对其进行一些简单的修改,并且介绍一些简单基础的操作,包装出红黑树这个数据结构,进而来模拟符合完美平衡性质的2-3查找树的种种性质。
二叉查找树
二叉查找树是一个比较基本且简单的数据结构,其有当前节点的值以及一些指向后驱节点的指针(因为是二叉查找树,所以包含两个后驱节点)构成,这里简单的列出其数据结构
typedef struct NODE { Value val; int number struct NODE *left, *right; } *Node;
对于该数据结构的操作,诸如插入、查找以及删除等,这里就不再赘述,会在后面介绍具有完美平衡性质的2-3查找树的对应操作时一并提及。
红黑树
这里首先介绍一下基于二叉查找树的红黑树的数据结构,然后在具体介绍和分析一下红黑树与2-3查找树之间的联系等。
实际上,之所以成为红黑树,是因为其将链接分为了红链接和黑链接。而一般情况下,通过想二叉查找树的节点添加color属性,从而通过链接指向的节点对应的属性来表明该链接的颜色——如果指向的节点的color属性为红色,则该链接为红色;如果指向的节点的color属性为黑色,则该链接为黑色。其余基本和二叉查找树没有太大的区别,因此其数据结构也基本和二叉查找树的数据结构差别不大,如下所示
typedef struct RBNODE { Value val; int number; int color; struct RBNODE *left, *right; } *RBNode;
所以看起来,实际上红黑树的数据结构和二叉查找树也没有什么大的区别。那么我们如何通过红黑树这个数据结构来模拟具有完美平衡的2-3查找树。实际上并不是十分的困难,这里的基本思路是普通的黑色链接仍然是链接两个2-节点(即普通的二叉查找结点);红色链接也链接普通的二叉查找节点,但是需要将其当作一个3-结点。这样子,我们就基于二叉查找结点,包装出了红黑树这个数据结构,从而可以模拟2-3查找树。可能说起来仍然比较抽象,这里我们通过示意图进行说明,如下所示
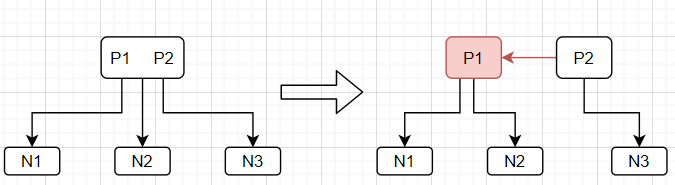
可以看到,在2-3查找树中,P1P2是一个3-节点;但是在对应的红黑树中,实际上3-节点是由两个2-节点和一个红链接构成的。这样子实际上基本就通过红黑树模拟了2-3查找树的数据结构了。
当然,对于红黑树这个抽象结构来说,为了更好地模拟完美平衡的2-3查找树,我们需要添加几条规则——否则如果任意设置红链接等,不方便进行操作,我们规定一个红黑树需要满足如下性质
1. 红链接均为左链接 2. 没有任何一个节点同时和两条红链接相连 3. 该树是完美黑色平衡的,即任意空链接到根节点的路径上的黑链接数量相等
实际上,这样子的红黑树就可以较好的模拟完美平衡的2-3查找树。
操作
实际上,我们在构建或者操作红黑树的时候,往往需要将基础的二叉查找树或者错误的红黑树转变为一个符合上述要求的红黑树,这里往往会用到左旋转、右旋转以及颜色转换等操作——实际上,基本通过红黑树模拟的完美平衡的2-3查找树,基本就是二叉查找树和上面那几个操作的组合而已,因此这里着重分析一下这几个操作。这里需要说明的是,我们下面的操作都要基于一个假设,当前的树是黑色完美平衡的,但是其无法满足其他红黑树的特性,因此我们需要通过下述的操作进行调整,从而使该黑色完美平衡的树转换为完美平衡的红黑树。实际上这个假设是很容易满足的——实际上从最开始博客中提到的插入或者删除操作,如果我们简单将其转换为红黑树的操作,则任何时候都是黑色平衡的,只不过是可能不满足红黑树的要求罢了(出现4-节点——即连续两个左连接为红链接、右链接为红链接),因此下面的操作是用来进行调整。
左旋转
这个操作的对象通常是红链接为右链接的节点的父节点,其效果是将红链接转变为左连接,且仍然保持局部性——仅仅改变该节点和其子节点的只想关系,其余节点并不发生变化(用来保持完美平衡性)。说起来比较抽象,这里首先给出对应的示意图,然后放出这部分的代码。
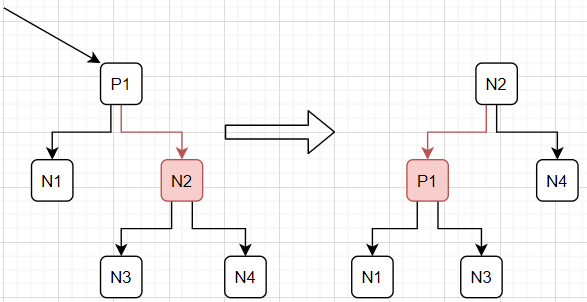
实际上,可以看到,一开始是指向N2节点的链接为红链接,即左连接为红链接;然后经过左旋转后转换为了指向P1节点的链接为红链接,即右连接为红链接。可以观察一下,除了P1和N2以外,其余的节点的情况没有发生任何变化(一个是子节点;另一个是从空链接到根节点的黑链接个数)。这里说明一下,完美平衡的2-3查找树对应的是完美黑色平衡的红黑树,也就是这里所有空链接到根节点的黑色链接个数相等。所以对于这个图来说,虽然N1的高度发生了变化,左旋后比左旋前高度高了1,但是这高的是红链接,所以黑色链接个数仍然不变。大家可以配合这张图进行理解,如图所示
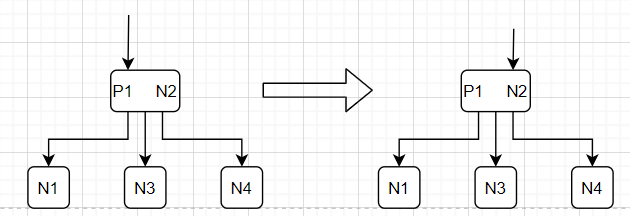
实际上我们可以将红链接抽象的3-节点画出来,如果我们想象这个3-节点的父节点的链接,那么左旋的意义相当于将该链接由指向P1更换为了指向N2,其余没有任何变化。但是对于我们的红黑树来说,却满足了我们之前提到的三个性质,因此这个左旋操作大概为这样。其具体的代码实现也很简单,如下所示
#define RED (1)
RBNode rotateLeft(RBNode node) { RBNode right = node->right; node->right = right->left; right->left = node; right->color = node->color; node->color = RED; right->number = node->number; node->number = Size(node->left) + Size(node->right) + 1; return right; }
可以结合代码和示意图看到,这个操作除了当前3-节点外没有修改其他任何节点的信息,从而完成了局部性调整。
右旋转
这个操作的对象通常是连续两个左子链接都是红链接的节点,其效果是将消除连续两个左子链接都是红链接,转换为当前节点的左连接和右链接为红链接,仍然保持局部性质,即仅仅父节点和两个左子节点的关系和链接,其余节点并不发生变化(用来保持完美平衡性)。说起来比较抽象,这里首先给出对应的示意图,然后放出这部分的代码。示意图如下所示
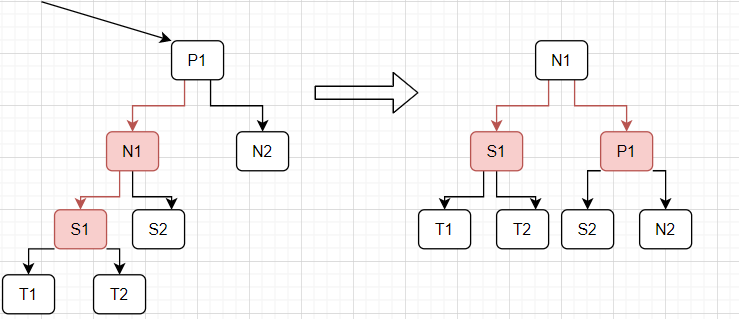
实际上,可以看到,一开始是指向N1节点、S1节点的链接皆为为红链接,即连续两个左子链接都为红链接;然后经过右旋转后转换为了指向S1节点、P1节点的链接为红链接,即左连接和右链接为红链接。可以观察一下,除了S1、P1和N1以外,其余的节点的情况没有发生任何变化(一个是子节点;另一个是从空链接到根节点的黑链接个数)。这里说明一下,完美平衡的2-3查找树对应的是完美黑色平衡的红黑树,也就是这里所有空链接到根节点的黑色链接个数相等。所以对于这个图来说,虽然T1、T2和N2节点的高度发生了变化,但是变换的主要是红链接,所以黑色链接个数仍然不变。大家可以配合这张图进行理解,如图所示
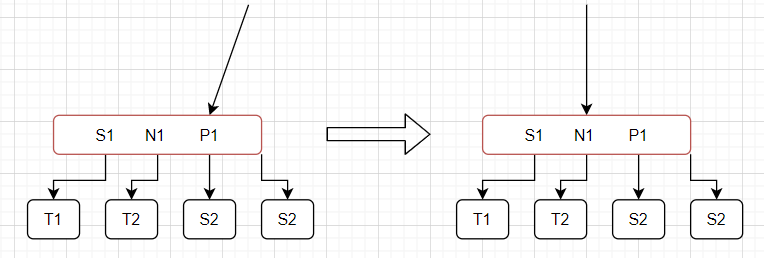
实际上我们可以将连续两个左链接为红链接抽象的4-节点画出来,如果我们想象这个4-节点的父节点的链接,那么右旋的意义相当于将该链接由指向P1更换为了指向N1,其余没有任何变化。但是对于我们的红黑树来说,虽然仍然不满足红黑树的性质,但是实际上如果我们直接把当前的节点N1提取出来融合到父节点上,则容易判断其仍然是满足完美平衡性质的,并且稍微修改节点的属性即可完成转变为符合要求的红黑树。因此右旋操作大概是这样。其具体的代码实现也很简单,如下所示
#define RED (1) RBNode rotateRight(RBNode node) { left = node->left; node->left = left->right; left->right = node; left->color = node->color; node->color = RED; left->number = node->number; node->number = Size(node->left) + Size(node->right) + 1; return left; }
颜色转换
实际上这个操作主要是用来调整上面的情况,其操作的对象是子左链接和子右链接结尾红链接的节点。其效果是将消除左右节点的红链接,转换为当前节点和其父节点的链接为红链接,仍然保持局部性质,即仅仅修改该节点、父节点和两个左子节点的关系和链接,其余节点并不发生变化(用来保持完美平衡性)。说起来比较抽象,这里首先给出对应的示意图,然后放出这部分的代码。示意图如下所示
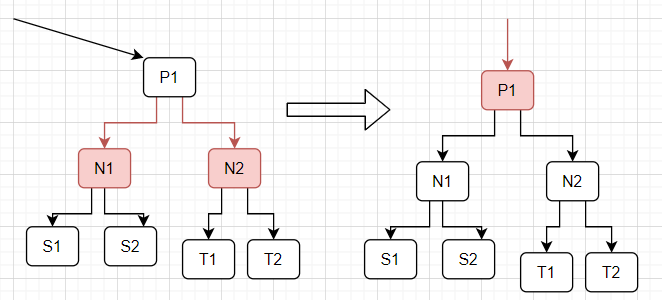
实际上,可以看到,一开始是P1节点指向N1节点、N2节点的链接皆为为红链接,即左子链接和右子链接都为红链接;然后经过颜色转换后转换为了指向P1节点的链接为红链接,P1节点指向其子节点的链接为黑链接。可以观察一下,除了N2、P1和N1以外,其余的节点的情况没有发生任何变化(一个是子节点;另一个是从空链接到根节点的黑链接个数)。这里说明一下,完美平衡的2-3查找树对应的是完美黑色平衡的红黑树,也就是这里所有空链接到根节点的黑色链接个数相等。大家可以配合这张图进行理解,如图所示
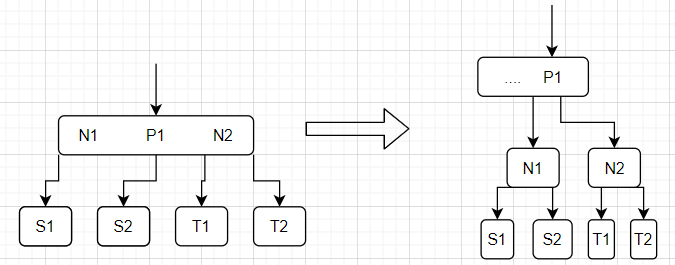
实际上我们可以将连左子链接和右子链接皆为红链接抽象的4-节点画出来,如果我们想象这个4-节点的父节点的链接,那么颜色转换的意义相当于将P1节点合并入其父节点上(父节点可能转变换为3-节点,可能转变为4-节点,也可能成为2-节点即转换为了根节点),其余没有任何变化。但是对于我们的红黑树来说,虽然仍然不满足红黑树的性质(父节点可能为4-节点),但是可以看到仍然满足大部分红黑树的要求,并且仍然是完美平衡的——其空链接到父节点的仍然相同。因此颜色转换操作大概是这样。其具体的代码实现也很简单,如下所示
#define BLACK (0) #define RED (1) void flipColors(RBNode node) { node->left->color = node->right->color = BLACK; node->color = BLACK; }
总结
实际上我们已经把从二叉查找树转换为红黑树所需要的操作讲述完毕了,大家已经可以结合前面分析和思想,构造出基于红黑树的完美平衡的2-3查找树了。这里面最重要的就是理解一下这几个操作的意义,我在说一下我在学习时的坑
1. 操作时始终保持黑色完美平衡——实际上在前面分析的时候,对于完美平衡的2-3查找树,我们的任何操作的任何时候,都保持着完美平衡,放到基于红黑树中的2-3查找树来说,就是始终需要保持黑色完美平衡,大家可以认真理解和思考一下。
2. 对于3-、4-节点的理解——我认为4-节点即为2个连续的红链接,可以是左右子节点的链接为红链接,也可以是一个子节点、一个父节点的链接为红链接,但是都可以抽象为4-节点。对于最后的基于红黑树的完美平衡的2-3查找树来说,是不允许存在4-节点的,但是根据前面的思路,我们首先会允许存在4-节点,在递归的时候,最后由下至上时,我们可以通过将4-节点的中间节点融合进父节点(就是上面介绍的颜色转换操作),从而消除4-节点为2个2-节点。
3. 注意完美平衡的性质——由于前面说过了,上一篇博客的所有对于2-3查找树的操作,都可以保持其完美平衡,也就是红黑树的黑色完美平衡,因此我们往往可以利用完美平衡的性质来化简所要分析的情况——如果有左子节点/右子节点,这一层上的节点都有子节点;如果左子节点/右子节点为空,则这一层所有节点都为空,需要注意利用一下这个性质,方便分析。需要注意的是,这个性质是从完美平衡的2-3查找树上说的,转换为红黑树的话,由于会有红链接存在,说法需要变换一下。如果有黑色的左子节点/右子节点,则必有对应的右子节点/左子节点,可以是红链接,也可以是黑链接。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号