算法入门——红黑树(一)
算法入门——红黑树(一)
2020-08-30 10:28:48 hawk
趁着疫情期间补习了一下计算机基础方面的知识,特别学习了一下算法知识。这里学习到红黑树时,其他操作都比较正常和可以理解,红黑树的删除操作直接把我学吐了。。借此机会稍微整理总结一下相关的知识,方便日后的学习。这里介绍的算法主要源自于《算法 第四版》,作者为Robert Sedgewick,我个人认为这是一本比较不错的算法书——虽然和我想象的算法书稍有不同。
概述
我们首先简单介绍一下相关的背景——我们知道,我们可以通过二叉查找树,快速的对数据进行管理,从而方便插入、查找以及删除等操作。但是在最坏的情况下,很可能二叉查找树会退化为链表,从而导致时间复杂度退化为O(n),这是让人不能接受的。我们当然可以对数据进行随机化处理后在进行管理,但是现实往往不允许这样做,因此我们引入平衡查找树,从而保证无论如何进行构造,关键步骤的时间复杂度都为O(lgn),也就是树高为O(lgn)级别。
为此,这里介绍的这种数据结构即为2-3查找树——需要声明的是,2-3查找树类似于伪代码,仅仅是一种算法思路,其实现有多种方式。在这里,由于前面提到了二叉查找树,因此根据计算机的传统,我们对于2-3查找树的实现通过复用二叉查找树,只需要在中间添加一个抽象层——红黑树(更具体的是左偏红黑树)即可。
因此,我们首先介绍一下2-3查找树的基本原理——这个是后面算法的主题思路,可以忽略一下实现的细节。然后我们在分析一下中间层——红黑树,也就是前面红黑树中的各种操作的实现代码,也就是二叉查找树的具体包装细节。这样子,我们最终即可完成平衡查找树的实现。
2-3查找树
定义
下面我们介绍一下2-3查找树。我们首先给出一下定义。虽然这些定义可能会很枯燥,但是一定需要认真理解。因为2-3查找树的性质可以推出很多原理,而这些原理是实现2-3查找树操作的理论基础。
一颗2-3查找树或为一颗空树,或由一下节点组成: 2-节点,含有一个键和两条链接 3-节点,含有两个键和三条链接
其节点类型大概如下所示。首先是3-节点,如下所示
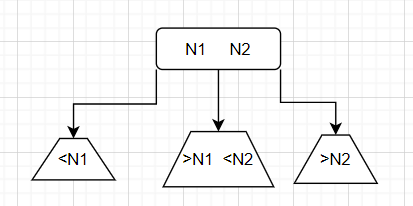
其次为2-节点,如下所示
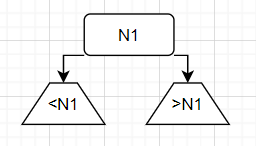
可以看到,这些节点之间还是比较容易理解的。除此之外,由于我们需要的是平衡二叉树,因此这里我们所谈论的2-3查找树,默认为完美平衡的2-3查找树,即所有空链接到根节点的距离都是相同的。这样我们也就基本介绍完了2-3查找树的基本定义,下面我们将介绍一下相关的操作,这里我们这涉及关键的操作,包括插入以及删除这三个操作,剩下的就比较简单,和二叉查找树基本没什么区别,中间层也就是照搬即可。
操作
如果没有完美平衡的2-3查找树这么个定义,那么实际上怎么操作都可以,自然最简单的就是按照二叉查找树的顺序去插入和删除即可。但是由于我们要求了是完美平衡的2-3查找树,那么简单的照搬二叉查找树的插入和删除就会出现问题,比如如果我们要删除完美平衡的2-3查找树的根节点S1(这里因为画图太麻烦了,所以只花了一部分,将就看一下),如下所示
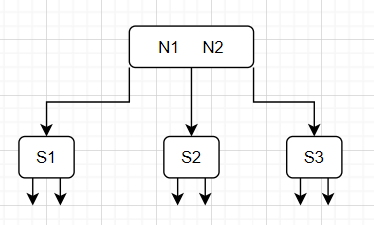
如果按照简单的二叉查找树的做法,直接删除,那么S1会被设置为空链接,那么这就会导致N1N2节点的子节点空链接到根节点的距离不同,从而破坏了完美平衡的2-3查找树的性质。但是在删除的过程中,我们进行一些额外的操作,在删除S1的时候同时变换父节点和其他子节点,如图所示

可以看到,该树的子节点空链接到根节点的距离仍然不变,其仍然为完美平衡的2-3查找树,符合对应的性质。下面我们将分别讲一下添加和删除的操作的规则思路。
添加
对于添加操作,需要说明实际上他并没有想象中的那么简单,比如如果此时所有的完美平衡的2-3查找树都是3-节点,如图所示

那最后无论如何调整,添加的这个子节点都会导致所有空链接到根节点的距离加1,也就是不仅仅需要将节点添加到对应的位置上,还需要调整其他节点的情况保证仍然满足完美平衡的2-3查找树。这里我们添加划分为两个步骤——自上向下的查找添加新节点和自下向上的调整其他节点,根据其特性我们可以使用递归进行操作,递归的大体模型如下所示
Node put(Node node, Key key, Value val) { //find and insert ... node->... = put(node->..., key, val); //balance the node ... }
对于插入操作来说,实际上其基本和二叉树的插入没有什么区别,根据键值判断下一个递归的位置即可。唯一需要说明的是,添加的时候是和最后一个节点进行合并的——皆如果最后一个节点是2-节点,则合并为3-节点;如果是3-节点,则暂时合并为4-节点。最后这些我们会统统在递归的调整部分进行调整,使其最后仍然满足完美平衡的2-3查找树。也就是可以简单的理解为,如果是新添加的节点,我们直接简单的合并到叶节点即可。我们还是给图(仍然为部分图,非从根开始的图),方便理解,如下所示
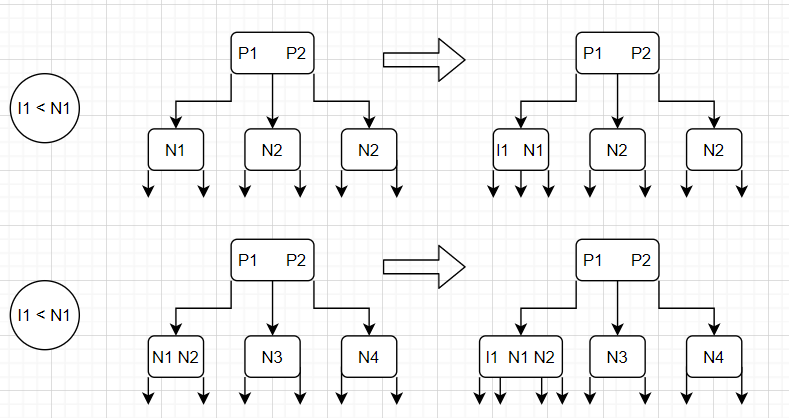
可以看到,经过插入操作后,实际上每一个空链接到根节点的距离仍然是不变的,并且这个插入操作基本不需要改变任何链表指向。那么下一步我们的步骤则是调整,我们与完美平衡的2-3查找树对比一下,就会发现我们中间会有一些4-节点(3个键和4个链接),因此实际上我们的调整即在保持完美平衡的基础上,拆分所有的4-节点。
下面我们分析一下调整操作,由于其是自下而上进行调整,并且由于链表的特殊性——我们的思路即将当前节点的子节点的4-节点中间键合并入当前节点内。可能仍然比较迷惑,没关系,我们首先在解释一下,如果还是比较抽象可以观察下面的图片理解。
由于我们一次处理一个插入,并且插入前树为完美平衡的2-3查找树,因此由下至上进行递归调整时,一次最多只有一个子节点为4-节点(可以为0个),因此只要我们将4-节点的中间节点合并入当前节点中,则在下一轮处理中可以处理这个情况,恰好为一个典型的递归。因此总的来说,这是一个比较巧妙的方法。我们给出一轮处理的图,如下所示
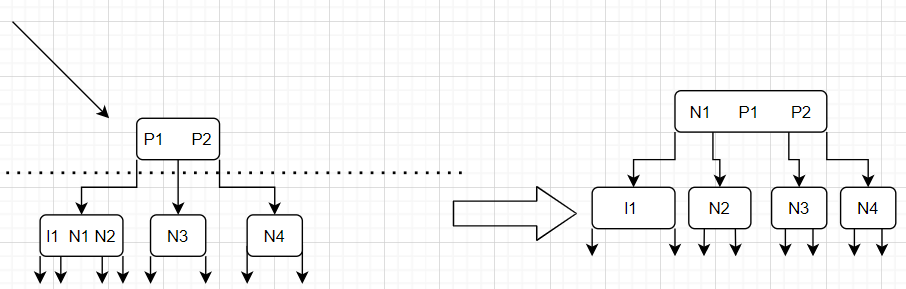
可以看到,当递归到P1P2节点时,其会处理子节点l1N1N2的4-节点,将中间值合并入P1P2节点。需要注意的是,当N1节点合并入P1P2节点的时候,其对应的子节点指向主要发生一定的改变,但并没有什么本质上的变化。这样子,对于下一轮递归来说,其将是N1P1P2节点的父节点处理N1P1P2节点这个4-节点。对于这一轮节点来说,可以看到,仍然没有改变空链接到根节点的距离,因此仍然保持着完美平衡的2-3查找树(如果递归结束的话)
这样子,通过这些操作,我们就完成了2-3查找树的添加操作,结果仍然保持为完美平衡的2-3查找树。这里需要说明的是,大家仍然只需要理解原理思路即可,不需要思考这些操作细节到底怎么处理,比如如何将N1节点合并入父节点中去等等。之后我们通过红黑树这个中间层,会以非常容易理解的方法,对二叉查找树的操作进行简单的组合,从而完成这里比较抽象的操作,无需过多担心。
删除
对于删除来说,实际上相比较添加,是有一些麻烦的——问题主要在,添加的话一定在叶子节点上(不考虑key已经存在,如果已经存在的话,删除在添加效果是一样的);但是删除的话可以是在任意位置,因此如果在任意位置下既保持完美平衡的特性,同时又删除掉这个键值是比较繁琐的——如果直接替代的话,想到与该被删节点的子空链接到根节点的距离被减少了1,而其他空链接到根节点的距离没变,则破坏了完美平衡的性质。
这里我们大概介绍一下整体思路,好有个整体认知,从而更好地理解问题。首先我们会将问题转换为叶节点的情形——即如果待删除节点为非叶节点的话,则用待删除节点的右子树中最小的节点(叶节点)进行覆盖(类似于二叉查找树的删除),这样子并没有改变完美平衡的特性,同时实际上也删除了该节点,然后问题就转换为了对于该待删除节点的右子树最小节点的删除——即叶节点的删除。而对于叶节点的删除,如果叶节点是3-的话,直接删除转换为2-节点即可,并不会影响空链接对于根节点的距离;如果是2-的话,删除的话则会导致该节点的子空链接到根节点的距离减一,因此最好的方法就是始终确保该叶节点为非2-节点即可。
那么也就是说,最后所有的问题,都归纳成如何确保递归遍历的节点始终为非2-节点(可以为3-节点为4-节点)。实际上这个问题也很简单,但是需要特别细心的分析——如果当前的节点为非叶节点,则必有子节点;同时根据完美平衡的特性,其必有左、右节点。这里我们就简单的以始终遍历最左侧的节点为例,其余和此情况没有什么区别,其主要操作如图所示
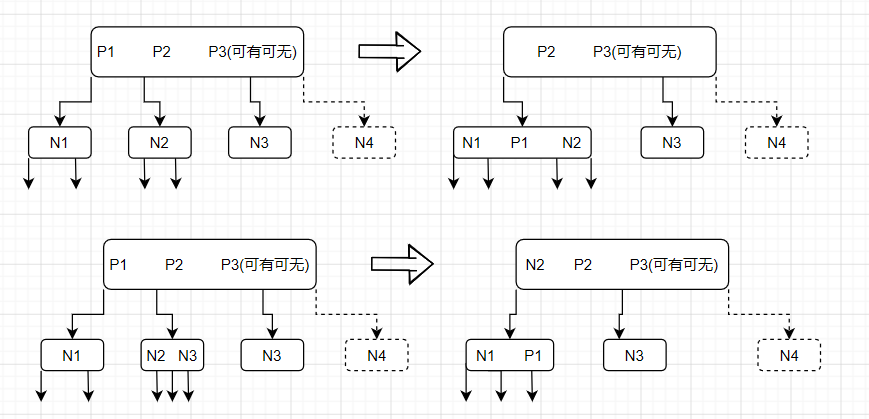
可以看到,实际上如果当前递归到P1P2节点(可能会有P3节点,无所谓)。由于下一个递归的是最左侧子节点(其余子节点情况类似),如果最左侧子节点为3-节点,则直接无需处理既满足非2-节点的要求了;如果最左侧子节点为2-节点,并且紧邻的子节点也为2-节点,则直接将其和当前节点的最小值合并即可,这样子既满足了下一个递归节点非2-节点的要求,同样保持了完美平衡性质(如果不这样,无法保持完美平衡性质。这里是一个难点,希望可以认真思考一下);如果最左侧子节点为2-节点,并且紧邻的子节点也为3-节点,则按照图中的样子进行变化即可,同样既满足了下一个递归节点非2-节点的要求,同样保持了完美平衡性质(如果不这样,无法保持完美平衡性质。这里仍然是一个难点,希望可以认真思考一下)。实际上只会遇到这几种情况,不会出现其他情况(因为剩下的子树仍然是完美平衡的2-3查找树)。
最后就变成了对于叶节点的删除,直接删除转变为2-节点/3-节点即可。然后我们利用插入时候的自下至上的平衡操作,重新在拆分所有的4-节点即可。根据前面的分析,最后仍然是完美平衡的2-3查找树。这样也就完成了删除操作。还是那句话,只需要理解原理和思路,对于实现的细节——比如里面的3-如何变为2-等细节完全不需要关心,只需要确保这个算法可以始终在删除要求节点后仍然能保持完美平衡即可,具体细节会在后面讲解,并且并不是很难。
总结
可能部分人看到这里后,仍然十分困惑。为什么要进行这么繁琐的步骤,为什么要分这么多情况,直接删除不行么?中间那些操作代码上怎么实现啊?或者还有没有可能由其他情况?首先,有困惑是正常的。这毕竟不是一个简单的算法。下面我再次对于完美平衡的2-3查找算法简单说明一下,希望能解决部分困惑,如果还是有问题的话,这也是正常的,可以多找找其他资料,自己在思考一下——因为我就是突然间思考中想明白的。
首先,这个完美平衡的2-3查找算法并不是具体的算法,而是一种思路——就比如栈:可以用数组实现,也可以用链表实现。但是核心的思想是一样的。这里其实现可以用左偏红黑树实现,也可以用其他的数据结构包装后实现,但是更具体的是要了解算法——即通过某些操作,我可以在实现插入、删除的目的下仍然保持完美平衡的2-3查找树的性质,具体那些操作怎么用代码实现我不需要关心。
除此之外,之所以会进行各种情况的考虑,是因为我们需要在操作完后仍然保持完美平衡的2-3查找树这个性质——这并不是一个很宽松的性质。一方面,要保持完美平衡——可以简单理解为所有的空链接在2-3树的同一级上,并且非空节点都是2-3类型的节点。想一想,如果随便插入一个节点而不做调整,插入的节点所对应的空链接自然高度加1,而其他的保持不变的话,则自然不满足完美平衡(根节点除外);删除的话是类似的,因此如果我们要进行插入或者删除,往往要对其他的节点进行操作,从而保证其他节点的子空链接的高度也会发生相应的变化。这就是情况复杂的原因。
而正是由于完美平衡的性质,则节点要么完全没有子节点,要么所有的子节点都存在,所以这样子实际上分析的情况也并没有那么多。何况添加和删除每一次仅仅操作一个,所以虽然情况仍然很多,但是基本不会有上述之外的情况。
之后我会具体讲解一下如果利用红黑树来实现完美平衡的2-3查找树。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号