ARC150E Weathercock 解题记录

题意：

给定一个长度为 \(n\) 的由 \(\texttt{L/R}\) 组成的序列 \(A\) 与一个正整数 \(m\)。

令序列 \(X\) 表示 \(A\) 重复 \(m\) 次的结果，接下来进行如下操作 \(10^{100}\) 次：

1. 考虑每个 \(L\)，如果其左边的 \(R\) 比 \(L\) 多，则打上反转标记。
2. 考虑每个 \(R\)，如果其右边的 \(L\) 比 \(R\) 多，则打上反转标记。
3. 把所有带有反转标记的位置反转。

计算 \(X\) 进行 \(k\) 次操作后，共计打上反转标记的次数。

\(1 \le n,m \le 2\times 10^5\)

---

手玩一下，初步的印象是 —— 一个元素至多会被改变 \(O(1)\) 次。

不妨设 \(R\) 的数量不少于 \(L\)。

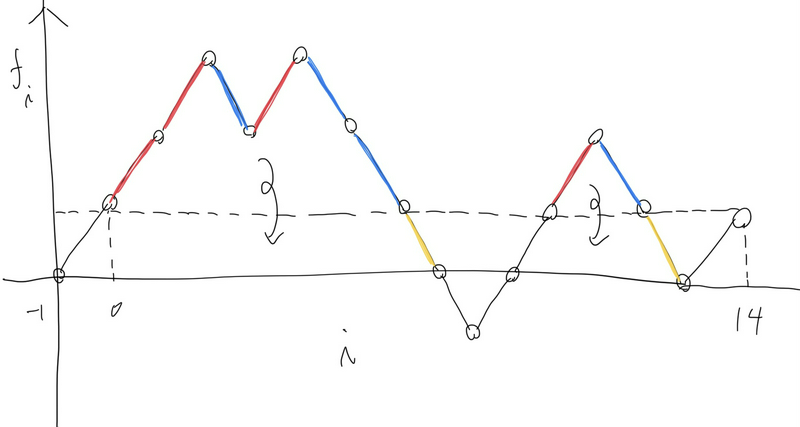
（图源为 atcoder 官方题解）

把 \(R\) 和 \(L\) 抽象成向上和向下的线段。

对应到操作上，相当于让 三种带颜色的边 都反转。

注意到 红边 和 蓝边 是一一对应的，我们只考虑黄边的影响。

也就是这次操作有意义的影响，其实只会让一些 \(L\) 变成 \(R\)。

显然，第一次操作后，最后一个位置成为了最高的位置。

其次，目前的 \(R\) 一定不会再变化了。

而对于一个 \(L\)，除非前面不存在比初始点高的位置，要不然一定变成 \(R\)。

模拟即可。