AGC 营业记录

仿照神仙们写做个 AGC 清单吧。

把自己以为有意思的题目搬上来。

之后可能考虑分开写。

[AGC001E] BBQ HARD \(\star\)

Difficulty: \(\color{blue}{\texttt{?}}\)

不会思维题。非常自闭。

容易发现这个式子等价于格路行走。

分别映射到左下角和右上角，然后 \(O(s^2)\) 做一次 dp 就好了。

[AGC001F] Wide Swap

Difficulty: \(\color{blue}{\texttt{?}}\)

🕊

[AGC002E] Candy Piles \(\star\)

Difficulty: \(\color{red}{2889}\)

小清新的博弈论。

首先容易发现题意等价于网格图上行走。

再观察一下，对于 \(x-y\) 相同的位置的胜负态一定相等。

于是做完了。

[AGC003E] Sequential operations on Sequence \(\star\)

Difficulty: \(\color{red}{2983}\)

感谢此题提醒我不是思维选手的事实。

容易令 \(q_i\) 单增。考虑倒推，每次计算插入一串的贡献。

这一串有一部分是上一个串的重复，还剩下某个长度为 \(l\) 的前缀。此时我们找到一个 \(q_x\) 使恰好比 \(l\) 小，那么就可以继续这个流程，且每次取模都是有意义的。

众所周知有意义的取模只有 \(\log\) 次，因此能做到 \(O(n\log^2 n)\)。

[AGC004E] Salvage Robots

Difficulty: \(\color{brown}{3205}\)

一开始想直接枚举矩形的左下角，后来发现好像能救的并不形成一个矩形。

但是有机会能救的一定是一个矩形，设当前向各个方向走的步数为 \(S_{0,1,2,3}\) ，然后记最大贡献为 \(dp_S\) ，考虑转移。

不妨考虑向上走，那么救到的人形成一个横着的竖条，显然可以 \(O(1)\) 转移。

于是就能做到 \(O(n^4)\) ，常数很小，可以轻松通过。

[AGC005D] ~K Perm Counting

Difficulty: \(\color{red}{2943}\)

考虑容斥。

首先拆成几条链。

对每条链计算钦定 \(i\) 个位置违反的代价，这个甚至可以 dp 。

最后拼到一起就好了。。

[AGC005E] Sugigma: The Showdown

Difficulty: \(\color{brown}{3276}\)

考虑在 \(B\) 树上的一条边，如果在 \(A\) 树上对应的两个点距离大于等于 \(3\) ，那么走到那里直接就赢了。

那么容易发现，如果 \(A\) 走了一步以后又往回走，显然就输了。

于是只需要模拟 \(A,B\) 走就行了。复杂度 \(O(n \log n)\)。

[AGC005F] Many Easy Problems

Difficulty: \(\color{brown}{3440}\)

考虑一条边何时产生贡献。

记这条边链接两端的 size 为 \(x\) 与 \(n-x\)，容斥，则对于集合大小为 \(k\) 时的贡献就是 \(\binom{x}{k}+\binom{n-x}{k}\)。

我们统计出所有可能的 size。记有 \(w_x\) 种情况令 size 为 \(x\)，那么容易有：

\[Ans_k=\sum_{i=k}^n w_i \binom{i}{k} \]

NTT 优化即可。

[AGC006E] Rotate 3x3

Difficulty: \(\color{red}{3101}\)

这题 xzy 好像在若干年前就会了，膜拜 xzy。

首先考虑一列，显然列包含的数字构成的集合不会改变，中间的数字也不会改变，此外每操作一次就交换上下的数字。

另外容易发现奇/偶数列只能内部交换，每次操作奇偶内部的逆序对数量奇偶性改变，而被交换上下的位置数目奇偶性也改变。于是随便判断一下就好了。

[AGC006F] Blackout \(\star\)

Difficulty: \(\color{brown}{3530}\)

转化一步题意：

现在给一张图，如果存在 \(a \rightarrow b \rightarrow c\)，你就能新建一条边 \(c \rightarrow a\)。

考虑什么时候会把一个连通块变成完全图，首先如果有一条双向边显然就变成完全图了。

考虑拓展，我们给出如下的结论：

如果存在从 \(a\) 到 \(b\) 的长度 \(\text{mod 3}\) 不同的路径，那么可以通过操作令 \(a \leftrightarrow b\)。

证明考虑归纳。

这启发我们对这张图三染色。注意到题目的性质，我们令 \(1 \rightarrow 2 \rightarrow 3 \rightarrow 1\)，然后如果不是完全图，那么对于任意的 \(C_x=1,C_y=2\) 都有 \(1 \rightarrow 2\)。剩下的情况类似。

注意一些特殊的情况。

[AGC007E] Shik and Travel

Difficulty: \(\color{gray}{3906}\)

首先考虑到一条合法的路径是一个 \(\text{dfs}\) 的过程，你每次可以随意选择一个子树走进去。

二分答案，我们需要每个子树满足条件的同时，合理的决定子树的行走顺序。

记 \(dp_{i,l}\) 表示子树 \(i\)，进入时长度为 \(l\)，出去时的最小长度。

容易发现对于相同的 \(dp\) 值，我们只需要保留 \(l\) 最小的。

有这样的推论：

记 \(cnt_x\) 表示点 \(x\) 的有意义的 \(dp\) 值数目，有：
\(cnt_x\leqslant 2\min\{cnt_{son_x}\}\)

事实上我们参考转移的过程就容易得到这一结论。

于是转移时点 \(x\) 我们可以双指针做到 \(O(\sum cnt_{son_x})\)，毛估估一下 \(O(n\log n)\)，因此直接转移就可以通过此题。

[AGC008D] K-th K

Difficulty: \(\color{goldenrod}{2164}\)

经典不会贪心。

按照每个数字钦定的位置贪心从前向后填，然后在从后向前填。

考虑这样的正确性：感觉好对啊（误

[AGC008E] Next or Nextnext \(\bigstar\)

Difficulty: \(\color{brown}{3559}\)

考虑这样一个事实，我们首先建立 \(i \rightarrow p_i\) 的边，这样形成了若干个环。

此外，我们考虑操作会带来的影响。建立另一张图包含 \(i \rightarrow a_i\) 的边，它一定是由上一张图经过某些操作得来的。现在我们得到了第二张图，需要复原出第一张图。

容易发现，我们抽出第一张图的一个环，做若干次操作后只有可能：

1. 没有变化。
2. 变成另外一个环（边数是奇数）或者分裂成两个环（边数为偶数）。
3. 变成一颗内向基环树。

考虑将第二张图的元素复原，对于一个环，你可以钦定它为操作 \(1\)，也可以钦定为操作 \(2\)。对于一颗基环树，我们需要考虑它能否复原，以及方案数。

设长度为 \(l\) 的环有 \(w\) 个，那么它的贡献就是：

\[\sum_{i=0}^{\frac{w}{2}}\binom{w}{2i}l^if_i2^{w-2i*(l\not=1 \and l\&1=1)} \]

其中 \(f\) 是合并的系数。

现在来考虑基环树的贡献，容易发现基环树的环上只会套链，考虑怎么把链合并进去。事实上容易发现有两种合并方法，但是需要满足空间足够。

\(O(n)\)。

[AGC008F] Black Radius \(\star\)

不妨先考虑每个点都是好的情况。

我们考虑每次染掉一个连通块时，在这个连通块的重心统计答案，即我们只计数令 \(d\) 最小的情况。

首先考虑到染全树的时候，可能有多个点满足 \(d\) 最小，所以我们分开计算这种情况。

对于一个点 \(x\)，有哪些 \(d\) 满足条件。记从 \(x\) 出发最远的点是 \(f_x\)，那么因为不能染全树，因此有 \(d < \text{dist}(x,f_x)\)。

我们考虑何时存在一组 \((y,d')=(x,d)\) 且 \(d' \le d\)。

给出结论：

如果不存在 \(y\) 在 \(x\) 邻域上且 \((y,d-1)=(x,d)\)，那么 \((x,d)\) 合法。

我们设 \((z,d')=(x,d)\)，通过仔细分析 \(x-z\) 路径长度的奇偶性即可得证。

现在已知了这个，那么记 \(g_x\) 为 \(x\) 向除了 \(f_x\) 方向的子树以外走最远的距离，我们还有 \(d-2 < \text{dist}{g_x}\)。

于是我们就解决了每个点都是好的情况。

假如有一些点不是好的，我们要扣掉这些贡献。具体来说，如果一个点 \(x\) 不是好的，我们对于每个原来会产生贡献的 \((x,d)\) 考虑能不能有另外一个点产生贡献。

显然如果覆盖了某一个有关键点的子树就必定可以有贡献。

换根维护上述内容即可解决。

[AGC009E] Eternal Average

Difficulty: \(\color{brown}{3428}\)

杜撰一下这题咋做。

容易将题意转化为一个 \(n+m\) 个叶子的树，第 \(i\) 层的 \(1\) 的贡献是 \(\dfrac{1}{k^i}\)，你需要计数贡献的种类数。

直接 dp 的困难在于难以描述目前的值。

实际上我们只需决定最后的值转化为 \(k\) 进制的形式。得到每层用了几个 0/1，考察是否能构造一个合法树就行了。

记 \(x_i\) 表示第 \(i\) 层用了几个 \(\texttt{1}\)，\(y_i\) 表示第 \(i\) 层用了几个 \(\texttt{0}\)，显然有：

\[\sum \dfrac{(x_i+y_i)}{k^i}=1\\ \sum x_i=n,\ \sum y_i=m \]

转成 \(k\) 进制的话，就要把同层的若干个 \(0/1\) 挪到上一层，也就是：

\[\sum \dfrac{(x_i+y_i)}{k^i}=1\\ \sum x_i=n-a(k-1),\ \sum y_i=m-b(k-1) \]

另外假设小数部分长度为 \(l\)，上面的条件等价于 \(\sum y_i=l(k-1)+1-\sigma x_i\)。

考虑 dp，记 \(dp_{i,j,0/1}\) 表示目前到第 \(i\) 位，\(\sigma x_i = j\) 的方案，目前是否是 \(0\)，即可解决。

[AGC010F] Tree Game

Difficulty: \(\color{red}{2897}\)

考虑 \(n=2\) 的情况，如果 \(A_1 \not = A_2\)，就把棋子放在多的那一边然后移，这样就能赢。

拓展到菊花，如果菊花的中心最小，那么随便把点放在一个更大的叶子，每次向菊花跑就能赢。否则就从菊花开始向最小的点跑，这样也一定能赢。

总结一下，能得到一下的结论：

如果一个点的值小于等于其每个邻域上的点，那么先手必负。

此时我们暴力 \(O(n^2)\) 枚举根就做完了。

以下是口胡：

我们考虑如何才能先手必胜。

如果从一个位置往大于等于自己权值的位置跑，显然是有害的，我们只能向更小的地方跑。

那么如果一个点走不动了就输了，这样就变成了 \(dag\) 上游走博弈。

拓扑排序即可。 \(O(n)\)

[AGC011D] Half Reflector

Difficulty: \(\color{red}{2931}\)

观察一下，首先连续的一段 \(AAAAAB\) 会变成 \(BBBBAB\)，而且除了被第一个位置挡住以外，都会从最后跑出来。

那么总结一下，每次都是左移一位再全取反。

[AGC011F] Train Service Planning

Difficulty: \(\color{gray}{3863}\)

考虑判断 \(-1\)，如果 \(b_i=1\) 而 \(2a_i>k\) 则显然不合法。

不妨先考虑 \(b_i=1\) 的情况：

显然，我们只需关心前 \(k\) 秒，火车的运行情况。对于每两行之间，我们需要插入两辆相向的火车，它们不能有交。

考察这样一种策略，我们令 \(1 \rightarrow n\) 的火车可以一趟走完而不停留，这一定是最优的。

感性的证明是，因为我们已经令去时最优了，而我们每令回来时减少 \(1\) 的代价，过去的时候就要增加 \(1\)。

于是只需要分配回来的火车，我们首先稍微平移一下区间，使得回来的形状类似竖直。

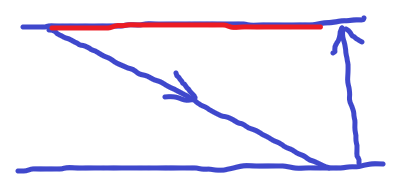
记 \(dp_{i,j}\) 表示在第 \(i\) 行，刚刚来到位置 \(j\) 时，最小花费时间。

上图的红色部分显然是 \(0\)。

其他部分的转移形如： \(dp_{i,j}=dp_{i+1,k}+(k\rightarrow j)\)

令 \(s_{i,j} = dp_{i,j}-j\)，我们有：

\(s_{i,j}=s_{i+1,k}+[k>j]\cdot len\)。

事实上，我们只需要拯救那些被限制的点就可以了。只转移最后被限制的位置 \(+1\) 的位置即可。使用线段树维护答案，时间复杂度为 \(O(n\log n)\)。

[AGC012E] Camel and Oases

Difficulty: \(\color{brown}{3490}\)

小清新的题。

令 \(dp_S\) 表示用了集合为 \(S\) 的操作最远走到哪里，容易得到一个 \(O(n\log V)\) 的做法。

对于多次的询问，容易发现只有 \(\log V\) 个合法的区间，于是做完了。

[AGC013D] Piling Up \(\star\)

Difficulty: \(\color{red}{3089}\)

膜拜 cdz ！！！

首先能想到一个 dp ，记 \(dp_{i,j}\) 表示拿了 \(i\) 个求，盒子里装了 \(j\) 个红球的答案。

但是我们其实不关心盒子里的情况，我们只关心转移的路径，如果这个相同就说明是相同的取出序列。

那么钦定必须走到底就可以了。

\(O(nm)\) 。

[AGC013E] Placing Squares

Difficulty: \(\color{brown}{3475}\)

等价于每个区间分别选两个点。

考虑转移，令 \(dp_{i,0/1/2}\) 表示位置 \(i\) 然后选了几个位置就有转移：

没有 \(\text{star}\) 的：

\[[dp_{i,0},dp_{i,1},dp_{i,2}] \begin{bmatrix}1&2&1\\1&1&1\\1&0&0\end{bmatrix} = [dp_{i+1,0},dp_{i+1,1},dp_{i+1,2}] \]

有 \(\text{star}\) 的：

\[[dp_{i,0},dp_{i,1},dp_{i,2}] \begin{bmatrix}1&2&1\\0&1&1\\0&0&0\end{bmatrix} = [dp_{i+1,0},dp_{i+1,1},dp_{i+1,2}] \]

然后维护矩阵幂就好了。

[AGC014E] Blue and Red Tree

Difficulty: \(\color{brown}{3312}\)

暴力用 \(set\) 启发式合并即可解决。

[AGC015D] A or...or B Problem

Difficulty: \(\color{orange}{2655}\)

考虑 \(l,r\) 的最高位，如果相同，显然可以一起去掉。

考虑 \(l=1\) 的情况，容易发现可以构造出任意最高位小于等于 \(r\) 的数。

否则相当于可以构造的数中间挖掉一块。递归下去即可。

[AGC015E] Mr.Aoki Incubator

Difficulty: \(\color{brown}{3571}\)

容易知道最后点一定按 \(v\) 排序。

观察题目，容易得到：点按照 \(v\) 排序后，每条线覆盖都形如一个区间。

一个点的区间两端就是它左右的运动速度相对最大的能相交的点。

另外容易发现相交的区间一定随着你选择的点移动而移动，做个 \(dp\) 就行了。

[AGC016D] XOR Replace \(\star\)

Difficulty: \(\color{red}{2910}\)

手玩一下，可以发现：

任意时刻，序列中数字构成的集合 都是 初始数字和它们的异或和构成的集合 的子集。

如果一开始把所有数字的异或和放在最后，那么一次操作就相当于交换某个位置和最后一个位置。

那么我们就只需要求解这个更加简单的问题了：

考虑如果序列是个排列，那么包括最后一个位置的环的贡献是 \(len-1\) ，否则就是 \(len+1\) 。

序列的情况类似，随便讨论一下就好了。

[AGC016E] Poor Turkeys

Difficulty: \(\color{red}{3029}\)

我们考虑维护集合 \(S_i\) 表示为了 \(i\) 存活，哪些鸡在此之前应该活着。（给它挡刀）

考虑这样一种维护方法，对于一只火鸡 \(x\)，如果此时 \(a,b\) 需要被处决一个，我们讨论：容易得到，如果 \(a,b\) 都在 \(S_x\) 中，那么 \(x\) 一定无法存活；否则如果有一方存在，则加入另一方。

考虑 \(x,y\) 如果都存活，那么它们的集合必须没有交，此时会发现这个条件充分而必要。

[AGC016F] Games on DAG

Difficulty: \(\color{gray}{3754}\)

容易发现题目等价于令 \(SG_1\not=SG_2\)。

我们设 \(dp_{S}\) 表示目前集合 \(S\) 之间的边没确定，且它们目前的 \(SG\) 值一致，直接 dp 即可。

\(O(3^n)\)。

[AGC017D] Game on Tree \(\star\)

Difficulty: \(\color{goldenrod}{2156}\)

典中典不会思维题，枯了。

大胆猜想一棵树的 sg 是它所有子树的 sg 加一的异或和，容易发现正确。

如何发现这个结论？

首先考虑根向下拉链的情况，容易发现这个等价于 nim 。

如果一个树的 sg 已经定下来了，就可以把它变成一条链。于是这个结论就非常显然了。

[AGC017E] Jigsaw \(\star\)

Difficulty: \(\color{red}{3158}\)

比较简单的 \(\text{E}\) 题，虽然我还是不会做。

容易使用一条边描述一个积木，相当于右侧的接口从某个变成了另外一个。

我们只需找到若干条首尾都合法的路径拼起来就行了。

现在考虑到有些点不能作为出发点，有些点不能作为结束点，也就是对它们的出入度数进行了限制，即 入度必须不大于出度/入度必须不小于出度 。

为什么这样就一定能找到合法路径呢，建立一个虚点用来补充出入度不相等的点，找到欧拉回路以后删掉虚点，容易发现合法。

另外需要排除形成环的情况。如果一个弱连通块的每个点都出入度平衡则只能形成环，需要排除。

时间复杂度 \(O(n)\)。因为只需要判断，所以实现也非常简单。

[AGC018D] Tree and Hamilton Path \(\star\)

Difficulty: \(\color{orange}{2757}\)

典中典不会思维题，枯了。

考虑哈密顿回路的情况，容易想到一条边的贡献是两边子树 \(size\) 的 \(\min\) 的两倍。

现在考虑删掉一条边。

有一个非常强的性质，就是删掉的边一定经过重心，且任何一个经过重心的边都可以删掉。

如果想到了这个限制就蛮好证明了，这里略去。

于是做完了。

[AGC018E] Sightseeing Plan \(\star\)

Difficulty: \(\color{gray}{3953}\)

有点复杂的题目，但是思考过程很直接。

首先考虑只有两个矩形的情况：

我们考虑从某个点出发会怎么样：

\[\sum_{i=X_0}^{X_1} \sum_{j=Y_0}^{Y_1} \binom{i+j}{i} \\ =\sum_{i=X_0}^{X_1} (\binom{i+Y_1+1}{i+1}-\binom{i+Y_0}{i+1}) \\ =\sum_{i=X_0}^{X_1} (\binom{i+Y_1+1}{Y_1}-\binom{i+Y_0}{Y_0-1}) \\ = \binom{X_1+Y_1+2}{Y_1+1}-\binom{X_0+Y_1+1}{Y_1+1}-\binom{X_1+Y_0+1}{Y_0}+\binom{X_0+Y_0}{Y_0} \]

容易发现等价于 \((X_1+1,Y_1+1)+(X_0,Y_0)-(X_0,Y_1+1)-(X_1+1,Y_0)\)。

这里括号的意义是走到一个离自己这么多距离的点的方案数。

容易发现对于任何一个点，它对应的四个点的坐标都是一致的。

我们现在考虑三个矩形的情况，从第二个矩形枚举一个点，然后分别对应到第一个矩形和第三个矩形，组合出 \(16\) 种情况计算一下贡献，\(O(n^2)\) 且常数巨大，过不了。

注意到我们本质上是枚举中间的点计算合法路径数，考虑转而枚举路径计算结果的合法中间点数。

我们把一条路径的合法点数拆开，进入时计算一次，出去时计算一次。这样我们就只需要分别枚举 \(O(n)\) 个入点和出点了。

[AGC019F] Yes or No \(\star\)

Difficulty: \(\color{gray}{3742}\)

小巧的数学题。

考虑放到坐标轴上，你会发现除了一定能拿到 \(\max(n,m)\) 的贡献，只要经过了 \(x=y\) 的线，你就能拿到 \(\dfrac{1}{2}\) 的贡献。

模拟即可。

[AGC018F] Two Trees \(\bigstar\)

挺好玩的讲课题。

考虑使用图论描述条件。

对于两棵树上的对应点，我们连一条不限流量的无向边。

对于树边，我们连一条流量为 \(1\) 的无向边，额外在两棵树的根上连一条流量为 \(1\) 的无向边。

这样，如果我们可以用一个欧拉回路构成这张图，就说是有解的。

具体的，第一棵树的点连向第二棵树的对应点的流量即为权值，树边代表着子树的权值和。

但是因为有不限流边所以不好求欧拉回路，考虑如果不限流边流量 \(>1\)，那么我们可以抽出一个环把它反向，这样就可以令流量 \(-2\)。

因此不限流边流量为 \(0/1\)，由子树大小的奇偶性决定。

求一次欧拉回路即可解决。\(O(n)\)

[AGC020D] Min Max Repetition \(\star\)

Difficluty: \(\color{red}{3062}\)

流泪了，为啥大家都觉得这题水啊/ll。

显而易见的是，我们可以计算出第二个条件规定的长度，记为 \(l\)。

如果 \(B\) 的数量比 \(A\) 多，则答案很显然。

否则，我们认为答案的形式一定为：

\(\texttt{[AAABAAABAA] [BBBABBBABBB]}\)

这样。虽然有点抽象，总之是只会由两段组成。

二分答案即可 😦

[AGC021E] Ball Eat Chameleons

Difficulty: \(\color{gray}{3944}\)

注意到我们要计数放球的方案数，考虑假如我们已知放球的序列，如何构造使得合法。

记一个变色龙的贡献是吃的红球数减蓝球数。那么一只变色龙要么产生 \(1\) 贡献要么产生 \(0\) 贡献，我们想尽量使得产生 \(0\) 贡献的变色龙更多。

因为我们只想让产生 \(0\) 贡献的变色龙尽量多，所以钦定它们都是 红+蓝。注意到当 \(r=b\) 时可能不一定能钦定到，特殊处理 \(r=b\)。

假设有 \(a\) 个变色龙产生 \(0\) 贡献，\(b\) 个变色龙产生 \(1\) 贡献，那必须红球必须比蓝球多 \(b\) 个。

我们把红球记为 \(+1\)，蓝球记为 \(-1\)。考虑一个前缀，如果值为负，表示至少有这么多的蓝球无法和红球匹配，即红球至少要比蓝球多这么多。

注意到一开始每个变色龙都是蓝色，因此即红球数加前缀最小值大于等于 \(n\)。

我们枚举总和，记有 \(a+b\) 个红球和 \(b\) 个蓝球，那么相当于我们从 \((0,0)\) 走到 \((a+2b,a)\) 且不能越过 \(x=X\) 这条线。使用经典的翻折法计算答案即可。

[AGC022D] Shopping \(\bigstar\)

Difficulty: \(\color{gray}{3866}\)

感觉好强的题！

首先容易发现能令购物时间对 \(2L\) 取模。接下来就不会了。

有一个性质是：显然答案只和列车走完全程的次数相关，因此这样就只有 \(4\) 种点了。

首先，如果一个点无论从哪侧进入都会从对面出来，那么不论如何都相当于列车走了一个全程。

另外，如果一个点从某个方向进入但会从同一个方向出来，那我们肯定想尽量这么做。

于是我们就能对左进左出和右进右出做匹配，每次匹配就能节约一轮。

这样就做完了。

另外注意到这样匹配本质上会导致下一轮的开始，因此需要留一个左进左出匹配起点。

钦定为最后一个点就可以了。

[AGC023D] Go Home \(\star\)

Difficulty: \(\color{red}{3173}\)

典中典不会思维题，枯了。

考虑最左侧和最右侧的人，容易发现人少的一定比人多的走得晚。

因此直接递归下去即可。

[AGC023E] Inversions \(\bigstar\)

Difficulty: \(\color{gray}{3653}\)

很有感觉的题，但是不太会做。

考虑计算方案数，记 \(cnt_w\) 表示 \(a_i\geqslant w\) 的数量，易得方案数为：

\[\prod_{i=1}^n (cnt_i - (n-i)) \]

枚举两个位置 \(i,j\)，考察它们是否产生贡献。

设 \(a_i\geqslant a_j\)，考虑到如果 \(p_i>p_j\) 不会产生贡献，可以令 \(a_i \rightarrow a_j\)，则产生的贡献是方案数的一半。

否则有 \(a_i < a_j\)，容斥一下就等价于上面了。

现在的问题是，我们需要计算：

\[\sum_{i=1}^n\sum_{j=i+1}^n[a_i \geqslant a_j]f(a_i,a_j) \]

\(f(x,y)\) 表示把一个 \(a\) 从 \(x\) 变成 \(y\)，此时的方案数。

预处理，有 \(f(x,y)=w\dfrac{s_x}{s_{y}}\)。

\[=w\sum_{i=1}^n\sum_{j=i+1}^n[a_i \geqslant a_j]\dfrac{s_{a_i}}{s_{a_{j}}} \]

树状数组维护即可。

[AGC023F] 01 on Tree

Difficulty: \(\color{red}{3148}\)

经典的贪心模型。

考虑能走 \(0\) 一定走 \(0\)，于是每个点都可以打包成 \(x\) 个 \(0\) 和 \(y\) 个 \(1\)。

对于点 \(a,b\)，我们分析决策顺序的贡献。

容易发现，只要：\(\dfrac{a_x}{a_y} \leqslant \dfrac{b_x}{b_y}\)，\(b\) 就一定优于 \(a\)。

这样，我们每次把最优的点合并入它的父亲就能得到答案。

[AGC024D] Isomorphism Freak

Difficulty: \(\color{goldenrod}{2307}\)

显然首先考虑直径，那么第一个答案显而易见。

可以发现答案上界毛估估一下是中心连出边的数量 * 最大子树叶子数。

但是显然不对。因为树形态产生的影响比较大。

因此考虑分治，每次把两个子树合并并使叶子数量取 \(\min\) 。易于发现这是最优的。

考虑合并的过程，记 \(dp_{i,j}\) 是使子树 \(i\) 和 \(j\) 同构的叶子 \(\min\) 。考虑转移。

显然这个不会莫名其妙新增多余的子树，因此二分图匹配即可。

因为直径为偶数时可能要换中心，所以总复杂度 \(O(n^4)\) 。

UPD:

发憨了。其实令直接深度相同的儿子数目相同即可。远不需要二分图匹配。

[AGC024E] Sequence Growing Hard

Difficulty: \(\color{red}{3001}\)

🕊

[AGC024F] Simple Subsequence Problem \(\star\)

Difficulty: \(\color{brown}{3544}\)

不会做，但感觉是人力能及的题人力不可及。

如果一个个枚举答案字符串再检查可以匹配多少给定字符串，感觉前途不大。

反过来匹配，考虑一次求出许多字符串的答案。

设 \(dp_{S1,S2}\) 为对于答案字符串集合，已经匹配的部分为 \(S1\) ，未被匹配的部为 \(S2\) ，其可以匹配的字符串集合大小。

形象的说，就是把一些字符串匹配的前一段算在了一起。

这样直接 dp 即可解决问题。（子序列自动机）

[AGC025C] Interval Game

Difficulty: \(\color{goldenrod}{2077}\)

考虑双方最优决策：

首先 A 肯定摆烂，走到最近的满足条件的地方。

那么 B 的选择方案就不可能让 A 连续向一个方向走。

所以 A 轨迹类似于 左-右-左-右 这样了。

也因此，两边线段内部的顺序就不那么重要了。

显然，右边的线段只有左端点有用，左边的线段只有右端点有用。

枚举这个分界点，显然可以 \(O(n+S)\) 求出答案。

排序复杂度 \(O(n \log n)\) ，总复杂度 \(O(n\log n + S)\)

[AGC025D] Choosing Points \(\star\)

Difficulty: \(\color{red}{2868}\)

感觉 nb 麻了。

这起码是铜牌吧。

考虑只有一个限制的情况，可以发现这是一个二分图。

感性的证明方法大概是发现不会出现奇环。

于是对两个限制分别染色，根据抽屉原理容易选出答案。

[AGC025E] Walking on a Tree

Difficulty: \(\color{brown}{3584}\)

感觉比 D 反而简单。

经典的分别考虑每条边，猜个结论产生的贡献是 \(\max(2,d)\) ，其中 \(d\) 是这条边上的路径数量。

证明非常显然。

juju 随便就切了 orz

[AGC025F] Addition and Andition \(\bigstar\)

Difficulty: \(\color{gray}{3936}\)

sto \(\text{s}\color{red}{\text{yzf2222}}\) orz 当场切

感觉比较 naive 但是自己想不到/ll

非常有 atcoder 风味的找规律题。

模拟工作的过程，可以发现有变化的位只有两边都是 \(1\) 的位和它的上一位。

然后容易发现两个 \(1\) 会变成 \(0\) 。

所以手动模拟最高位的并排的 \(1\) ，然后后面的并排的 \(1\) 就相当于每次向上移了。

可以手玩一下辅助理解。

[AGC026D] Histogram Coloring

Difficulty: \(\color{orange}{2746}\)

对于每一行把颜色相同的相邻位置并到一起然后从上往下 dp 即可。

容易发现一段如果红蓝相间则有两种转移方法，否则只能对上面取反。

[AGC026E] Synchronized Subsequence

Difficulty: \(\color{red}{3016}\)

感觉比较轻松的题目。

首先考虑把原串划分为若干个 \(a,b\) 数目相等的串，然后依次考虑每段。

对于一段 \(a\) 在 \(b\) 前的段最优选法肯定形如 \(ababab\) 。

否则就要选择一段前缀 \(b-a\) 数量最大的，考虑到这样选一定是形如 \(bbbbbbaabaaabbaaaa\) 即一段长的 \(b\) 接一段乱序，然后这个乱序其实就是一组后缀。

找到最优的后缀然后贪心选就行了。

[AGC026F] Manju Game \(\star\)

Difficulty: \(\color{gray}{3704}\)

考虑对长度的奇偶性讨论。

首先感性的，如果在一次操作后自己失去了先手肯定不优秀。

具体的，这个策略肯定劣于在端点取。

因此对于 \(n\) 为偶数，最优的策略一定是在一端取。

接下来考虑 \(n\) 为奇数：

首先肯定是在偶数位置取，接下来后手可以选择另外一侧的奇数位置拿走。

然后在某个时刻先手就可以选择直接拿走奇数位置走人。

于是先手就能得到一段偶数位置+奇数位置+偶数位置。

那么考虑二分先手能取得的贡献大小 \(w\) ，然后用偶数位置把序列分开，要求任何一段产生的额外贡献都大于 \(w\) 即可。

[AGC027D] Modulo Matrix

Difficulty: \(\color{red}{2984}\)

直接按对角线讨论即可。

[AGC027E] ABBreviate \(\bigstar\)

Difficulty: \(\color{gray}{3634}\)

套路的考虑给定 \(S\) 和 \(T\) 问能否表示。

首先找到一个粗略的估计条件。

分别给 \(A,B\) 赋值为 \(1,2\) ，容易得到每次操作后序列 mod 3 的值不变。

这样，贪心的把 \(S\) 的最短的一个前缀变成 \(T\) 的一个字母，如果剩余的 \(S\ mod\ 3 = 0\) 就可行。

注意判断一开始就动不了的情况。

那么我们可以方便的判断两个串能否相互转化了，且容易发现上面的转化方式最优。

因此直接使用上述方法进行 dp 即可解决此题。

Almost similar: ARC110E

[AGC027F] Grafting \(\bigstar\)

Difficulty: \(\color{brown}{3544}\)

感觉巨大nb的题。

遇到这种题可能感觉难以下手，因为决策的性质太烂了。

那么首先要确定一个根：

考虑唯一一个可以用的性质，一个点只能移动一次。

于是我们枚举移动的点，然后它就固定了。

这样我们得到了一个 root 。

因为一个点只会移动一次，那么移动的位置都固定了，因此我们只要关心移动的顺序。

所以只需要用拓扑排序维护移动顺序即可。

[AGC028C] Min Cost Cycle

Difficulty: \(\color{orange}{2463}\)

以为是什么高妙自动机，发现是搜索/kk

直接折半搜索即可通过。

[AGC028E] High Elements

Difficulty: \(\color{gold}{4145}\)

称一个元素是好的，当且仅当它在原序列是前缀最大值。

我们尝试一个个将元素插入，容易知道插入好的元素一定有贡献，且任何时候两个序列的顶端至少有一个是好的。

贪心的把元素放入第一个序列里，接下来只需考虑能否摆放之后的元素令有合法解。

容易发现，我们可以令之后的元素中，某一侧只有好的元素有贡献。

接下来的一步有点感觉，假设 \(A\) 侧需比 \(B\) 侧多放 \(x\) 个，接下来还有 \(w\) 个好元素，我们钦定 \(A\) 侧有 \(t\) 个非好元素产生贡献，\(s\) 个好元素产生贡献。就有：

\[x=t+s-(w-s)\\ 2s+t=x+w \]

注意到 \(x+w\) 是常数，只需考虑能否在之后的元素中选出合适的 \(2s+t\) 即可。

计算出以每个元素作为开始能否选出贡献为 \(v\) 的元素即可。

注意到我们可以通过【减少一个好元素】的方式调控这个贡献。于是只需对奇偶的情况分别维护最大贡献就好了。

[AGC029D] Grid game

Difficulty: \(\color{goldenrod}{2033}\)

容易发现高木每轮必须移动。

直接 dp 即可解决。

[AGC029E] Wandering TKHS \(\star\)

Difficulty: \(\color{red}{3088}\)

感觉挺有意思的题目。

枚举每个节点开始移动，容易做到 \(O(n^2\log n)\) 。

考虑经典的套路，重复利用之前的信息。

对于一个点 \(x\) ，记 \(1 - x\) 之间的最大编号节点为 \(w_x\)，离 \(w_x\) 最近的 \(x\) 一侧的点是 \(d_x\)。

我们有 \(Ans_x=Ans_{d_x}\)，具体的，考虑到这两个点都被 "关在了最大值为 \(w_x\) 的一个区域中"，它们在突破 \(w_x\) 之前一定都会走满这个区域，而往 \(w_x\) 方向的答案可以在 \(w_x\) 处就计算出。

记 \(w_x - 1\) 的路径上（不含 \(w_x\)）的最大值为 \(S\)，那么 dfs 一次 \(w_x\) 内部一侧的点即可得到 \(w_x\) 内部的答案，而外部的答案可以通过 \(w_{w_x}\) 的答案得到。

于是只需要对每个能成为 \(w_x\) 的点向下找到能到达的所有位置即可。

容易发现，整棵树只会被累计搜索一次。

均摊 \(O(n)\) 。

[AGC030D] Wandering TKHS

Difficulty: \(\color{orange}{2602}\)

感谢周指导的指导。

直接 dp 即可解决。

[AGC030E] Less than 3 \(\star\)

Difficulty: \(\color{gray}{3753}\)

如果我们把相同的数字合并到一起，那么这个操作不会在中间插入一个新的段。

插入一个新的段只能在两端。

枚举一下匹配的情况就行了，复杂度 \(O(n^2)\)。

[AGC030F] Permutation and Minimum \(\star\)

Difficulty: \(\color{brown}{3474}\)

考试题。

顺便记录一下。

首先去掉 \((x,y)\) 的，记 \((x,-1),(-1,x)\) 有 \(a\) 个，\((-1,-1)\) 有 \(b\) 个。

考虑从大往小填，设 \(dp_{i,j,k}\) 表示填了 \([i,n]\) ，目前有 \(j\) 个 \((-1,-1)\) 以及 \(k\) 个 \((-1,x)\ \ (x<i)\) 。

直接转移即可。

[AGC031D] A Sequence of Permutations \(\bigstar\)

Difficuly: \(\color{red}{2975}\)

首先记排列的复合为 \(\circ\) ，那么有 \(F(a,b)=b\circ a^{-1}\) 。以下会省略这个符号。

玩出前若干项得到：

\[a_1=p\\ a_2=q\\ a_3=qp^{-1}\\ a_4=qp^{-1}q^{-1}\\ a_5=qp^{-1}q^{-1}pq^{-1}\\ a_6=qp^{-1}q^{-1}p^2q^{-1}\\ a_7=qp^{-1}q^{-1}pqpq^{-1}\\ a_8=qp^{-1}q^{-1}pqp^{-1}qpq^{-1}\\ a_9=qp^{-1}q^{-1}pqp^{-2}qpq^{-1}\\ a_{10}=qp^{-1}q^{-1}pqp^{-1}q^{-1}p^{-1}qpq^{-1}\\ \cdots \]

（充满勇气的）写下去，然后到这里应该能发现规律了。

首先值得注意的是容易发现一个不变的前缀形如：

\(q,qp^{-1},qp^{-1}q^{-1},qp^{-1}q^{-1}p,qp^{-1}q^{-1}pq\dots\)

这个东西是循环 \(qp^{-1}q^{-1}p\) 的。

另外写到一定长度以后也能发现后缀的循环节，是 \(p^{-1}qpq^{-1}\) 。

综合这两个规律直接得到 \(a_{x}=(qp^{-1}q^{-1}p)(a_{x-6})(p^{-1}qpq^{-1})\) 。

[AGC031E] Snuke the Phantom Thief

Difficulty: \(\color{silver}{3689}\)

考虑流。

首先如果只有 1,3 限制，有一个经典的建模，就是直接把点放在坐标系上，x 轴向点连，点向 y 轴连。
现在考虑有 2,4 操作，我们只需要枚举一共拿了多少个，就可以转化成上下界的形式。

以上是口胡。

另外一种做法并不需要上下界，我们枚举一共拿了多少个，考虑一维的情况。

事实上限制 " \(x\) 坐标小于等于 \(a_i\) 的最多拿 \(b_i\) 个 " 等价于我们对 \(x\) 排序后，\(b_i+1\) 之后拿的 \(x\) 坐标必须大于 \(a_i\)。

类似的限制 " \(x\) 坐标小于等于 \(a_i\) 的最多拿 \(b_i\) 个 " 这种条件。

对于二维的情况，我们将对 \(x\) 排序的数组与对 \(y\) 排序的数组进行匹配。把点放中间向两边连即可。

[AGC032E] Modulo Pairing

Difficulty: \(\color{brown}{3402}\)

弱智题。

二分分界点，每边纪念品分组。

[AGC033D] Complexity \(\star\)

Difficulty: \(\color{red}{2958}\)

大套路题，但是我不会。

考虑一个朴素的 dp 即 \(dp_{a,b,c,d}\) 表示一个矩形的凌乱度，然后用二分大力转移。

这样就是 \(O(n^4\log n)\) 。

容易发现凌乱度只有 \(\log\) 级别，最多只有 \(16\) 。

记 \(dp_{a,b,c,k}\) 表示行 \([a,b]\) 左列为 \(c\) 时，右列的最大值满足凌乱度最多为 \(k\) 。

考虑转移，如果是横向的合并则可以 \(O(1)\) ，纵向合并的话，鵺可以二分。

因此 \(O(n^3\log^2 n)\) 。

[AGC033E] Go around a Circle

Difficulty: \(\color{red}{3103}\)

一眼上去好像很不可做的样子。

发掘一下性质，首先不妨设开头是 \(R\)，那么环上显然不能有 \(BB\)。

假如开头是 \(RB\)，那么环上还不能有 \(RRB\) 或者 \(BRR\)。容易发现此时满足条件的环只有 \(BRBR\dots\) 或者 \(RBRB\dots\)。显然这两个环满足任意条件，即答案为 \(2\)。

接下来讨论开头由 \(a\) 个 \(R\) 和一个 \(B\) 的组成会产生什么影响。

假设 \(a=2k+1\)，那么就要求连续的 \(R\) 段的长度必须要是奇数，而且长度不超过 \(2k+1\)。

假设 \(a=2k\)，那么连续的 \(R\) 段的长度必须要是奇数，而且长度不能超过 \(2k+1\)。

考虑到在第一个 \(B\) 以后你一定能走到环上的 \(B\) 旁边，所以对于后面的 \(R\) 连续段，假如长度为奇数相当于再次限制了环上连续 \(R\) 的长度，否则没有限制。

那么直接 \(dp\) 即可解决。

[AGC034D] Manhattan Max Matching

Difficulty: \(\color{gray}{3665}\)

最近总是做不出大套路题，看来需要加深做题和讨论了。

拆开曼哈顿距离的柿子然后大力费用流即可。

[AGC034E] Complete Compress

Difficluty: \(\color{orange}{2637}\)

直接枚举中心点在哪即可做到 \(O(n^2)\)，换根可以 \(O(n)\)。

[AGC035D] Add and Remove \(\bigstar\)

Difficulty: \(\color{red}{2902}\)

找到被 AGC 乱杀的感觉了。

考虑一个容易想到的 \(dp\) ，即记 \(dp_{l,r,a,b}\) 表示消除 \([l,r]\) 后左边产生 \(a\) 倍贡献右边产生 \(b\) 倍贡献，这种情况的最小值，转移只需枚举最后一个被消除的位置。

结论是状态总数只有 \(O(n2^n)\) 级别。

考虑到 \(a,b\) 都只和另外一侧是否产生贡献有关，感性理解一下确实很对。

具体的说，在枚举一个

🕊

[AGC035E] Develop \(\star\)

Difficulty: \(\color{gray}{3720}\)

考虑一个这样的事，假设我们想删除一些点，如果它们的转化关系构成了环则显然无法删掉。否则我们就可以按照拓扑序删除。

那么，不妨考虑如何才会构成环。一种情况是 \(k\) 为偶数，此时只有奇偶性相同的数字之间才可能构成环。于是可以令 \(k \rightarrow k/2\)，那么条件就等价于你不能选 \(k+1\) 个连续的数字，可以简单计算。

类似的，对于 \(k\) 为奇数，我们也能记下偶数的连续数量和奇数的连续数量，直接转移即可 \(O(n^3)\)。

[AGC036D] Negative Cycle \(\bigstar\)

Difficulty: \(\color{brown}{3326}\)

感觉非常强的题。

考虑使用一个差分约束来描述这个问题，那么我们需要给每个位置分配一个权值，然后如果某条边不符合这个权值情况就删掉。

首先要满足 \(0\) 边的条件即 \(a_i\leqslant a_{i+1}\) 。

记 \(p_i=a_{i-1}-a_{i}\) ，那么取得贡献的要求就是：

取得 \(i \stackrel{1}\longrightarrow j\) 的权值当且仅当 \(a_i+1\geqslant a_j\) 即 \(p_i+\cdots +p_{j-1}\leqslant 1\) 。

取得 \(i \stackrel{-1}\longrightarrow j\) 的权值当且仅当 \(a_i-1\geqslant a_j\) 即 \(p_i+\cdots +p_{j-1}\geqslant 1\) 。

容易发现 \(p\) 的最优取值只有 \(\{0,1\}\) ，然后发现转移只和之前的两个 \(1\) 有关，因此考虑 \(dp\) 并记下之前 \(1\) 的出现位置就行了。

实现精细一点能做到 \(O(n^3)\) 。

[AGC036E] ABC String \(\bigstar\)

Difficulty: \(\color{gray}{3783}\)

非常神秘的一个题！！

注意到可以把相同的字符合并到一起，那么此时记 \(cnt_{s}\) 表示字符 \(s\) 的出现次数，方便起见，令 \(cnt_a \leqslant cnt_b \leqslant cnt_c\)。

接下来，容易发现最优解能保留 \(3cnt_a\) 个字符，我们尝试构造它。首先保留所有的 \(a\)，那么字符串就被分成了 \(cnt_a+1\) 个部分，每个部分要么只有 \(b\)，记数量为 \(w_1\)，要么只有 \(c\)，记数量为 \(w_2\)，要么都有，记数量为 \(w_3\)。

   结论：如果$w_1+w_3 \geqslant w_2$，则能做到保留 $cnt_a$ 个字符。

事实上，从感性上就易于得到该结论。下面给出简略的证明。

我们尝试找到一种逐渐删除字符串一些元素的方法，最后得到我们需要的解。

首先，我们尝试令 \(cnt_b=cnt_c\)。

对于一个 \(b,c\) 都存在的段，它一定形如 \(bcbcbc\cdots / cbcbcbc \cdots\)。

接下来，对于一个这样的串，我们就把它变成 \(ABCBCBA\)，直到 \(cnt_b=cnt_c\)。注意到每个含有 \(b,c\) 的串，我们都有 \(1\) 的贡献，而 \(w_1+w_3\geqslant w_2\)，所以一定能达成。

接下来我们就能删掉连续的 \(BC/CB\) 直到 \(cnt_a=cnt_b=cnt_c\)，这样我们就完成了构造。

对于不满足上述结论的情况，我们就需要删除一些 \(A\)。最优的做法显然是打破只含有 \(C\) 的间隔。

[AGC038D] Unique Path

Difficulty: \(\color{orange}{2628}\)

感觉萌题。但是我不会 /ll

大致思路是考虑 \(0,1\) 的传递性，然后先合并 \(0\) 边并分类讨论。

[AGC038E] Gachapon \(\star\)

一眼 min-max 容斥，假如我们直接 min-max 容斥，就要考虑一个子集的 \(\min\) 答案。

对于某个子集，可以用一个系数描述集合之外的贡献，接下来只需直接统计此集合的答案。枚举选择的次数，统计截止次数之前还没有取到答案的方案数，可以使用 \(dp\) 解决。

另外也可以使用生成函数方法。记 \(P_i=\frac{a_i}{S}\)。首先容易发现这是一个序列拼接模型，我们首先描述某个数字序列的生成函数。因为要求出现次数大于等于 \(B_i\)，可以得到生成函数为：

\[F_i(x)=\sum_{j=B_i} \dfrac{(xP_i)^j}{j!}\\ =e^{xP_i}-\sum_{j=0}^{B_i-1} \dfrac{(xP_i)^j}{j!} \]

我们所求即为 \(\prod_i F_i(x)\)，表示某个回合已经结束的概率。

因为轮数可能非常大，直接乘肯定不行，要带着 \(e\) 跑。我们 \(dp\) 算出 \(e^{n}{S}\) 的系数 \(G_n(x)\)，接下来就可以表示答案了。

\[Ans=\sum_{i=0}(1-i)) \]

对于无限求和式，一般的做法是把限制更大的交换求和次序至后面单独处理。但在此之前，先让我们消去常数。

\[=\sum_{j=0}^S\sum_{i=0}(1-i![x^i]e^\frac{j}{S}G_j(x))\\ =\sum_{j=0}^S\sum_{i=0}(1-i!\sum_{k=0}^i\dfrac{g_{j,k}(\frac{j}{S})^{i-k}}{(i-k)!})\\ =-\sum_{j=0}^{S-1}\sum_{i=0}(i!\sum_{k=0}^S\dfrac{g_{j,k}(\frac{j}{S})^{i-k}}{(i-k)!})\\ =-\sum_{j=0}^{S-1}\sum_{k=0}^Sg_{j,k}(\frac{j}{S})^{-k}k!\sum_{i=0}(\frac{j}{S})^{i}\binom{i}{k}\\ \]

有这样的组合恒等式：

\[\sum_i a^i\binom{i}{b}=\dfrac{1}{(1-ax)^{n-b+1}} \]

于是就可以快速计算了。

[AGC039E] Pairing Points \(\star\)

Difficulty: \(\color{brown}{3430}\)

比较神秘的 dp 题。

[AGC040F] Two Pieces \(\bigstar\)

Difficulty: \(\color{blue}{\texttt{?}}\)

容易想到拍到二维平面上，那么操作大概是下图的样子：

那么就是要从 \((0,0)\) 走到 \((A,B)\) 而且要求步数为 \(n\) 。

假如只有红色操作显然是卡特兰数，但是如果加上蓝色操作会导致难以描述目前消耗的步数以及位置。

注意到红色操作永远不能碰到线 \(x=y\) ，现在考虑一个和蓝色操作等价的操作，即把限制不能超过的那条 \(x=y\) 的直线拉到自己这里来，那么以后的行动轨迹就不能碰到它。

这样如果我们枚举最后一次使用蓝色操作的位置，那一方面我们可以知道此时终点的位置，另一方面还能知道蓝色操作的使用次数。

考虑另外一方面，即因为红色操作不能碰到分界线，所以蓝色操作一定是一起做的，又知道蓝色操作的总次数，因此答案即：红色操作的形态（折线法）乘以蓝色操作的使用情况，插板法解决即可。

[AGC041D] Problem Scores \(\bigstar\)

Difficulty: \(\color{red}{3096}\)

感觉很强的题目。

首先肯定转化为前一半比后一半的答案更大。

接下来如果正常的做应该只能做到最优 \(O(n^2\ln n)\) 。

现在考虑转化为每次进行后缀减，然后算出会产生的贡献，相当于做背包。

容易发现背包容积是 \(n\) ，所以随便做力。

[AGC041E] Balancing Network

Difficulty: \(\color{brown}{3502}\)

小清新分讨，感觉 easy 。

首先考虑更简单的 \(T=2\) ，容易想到只维护三个位置即可。

对于 \(T=1\) ，压 \(64\) 位暴力模拟即可。

[AGC043D] Merge Triplets \(\star\)

Difficulty: \(\color{orange}{2708}\)

感觉很强的题目。

首先考虑到每个序列内都可以按照前缀最大值划分成若干个段，而容易发现这些段在最终的序列内都是连续的。

如果我们已经决定好段的样子，那么不用管它们拼接的方法，最终生成的序列都是一致的。

因此直接对这个东西 dp 即可。

\(O(n^2)\)

[AGC044C] Strange Dance \(\bigstar\)

Difficulty: \(\color{red}{2889}\)

膜拜 xzy ！！！

容易想到使用 dp 解决。

提供另外一种思路：

考虑用一颗 trie 维护每个位置，满足一个位置的值相当于根到它的路径 \(\text{reverse}\) 后的值。

那么操作分别相当于：交换子树 1/2 并打上 tag ，或者轮换子树然后向子树 \(0\) 递归。

直接维护即可。

[AGC044D] Guess the Password \(\star\)

Difficulty: \(\color{red}{3165}\)

好玩题。

容易得到每个字符的出现次数，现在考虑如何得到答案。

每次选取 size 最小的两个合并到一起就行了。

[AGC044E] Random Pawn \(\bigstar\)

Difficulty: \(\color{brown}{3599}\)

好 nb 的题目，记录一下。

从 \(a_i\) 最大处断环成链。

容易发现一个点的决策无论目前的花费都只有一种。

不妨先决策哪些点是停留，记这些点 \(is_i=1\) ，那么一个点的答案就是：

\[ans_i= \begin{cases} a_i&is_i=1\\\\ \dfrac{ans_{i-1}+ans_{i+1}}{2}-b_i&is_i=0 \end{cases} \]

不妨令 \(b_i=0\) ：

考虑 \(is_x=1,is_y=1\) 且 \(\forall i\in(x,y)\ is_i=0\) ，容易发现：

\(\forall i\in[x,y]\ ans_{i}=\dfrac{a_x(y-i)+a_y(i-x)}{y-x}\)

具体的说，就是 \(ans_{i}\) 是过 \((x,a_x)\) 和 \((y,a_y)\) 两点的直线， \(x=i\) 时 \(y\) 的值。

于是只需要选出一个上凸壳即可。

那么对于 \(b_i\not = 0\) 只需要给每个位置一个偏移使得满足条件即可。

记这个偏移为 \(c_i\) 就能列出如下柿子：

\[ans_i-c_i= \begin{cases} a_i&is_i=1\\\\ \dfrac{ans_{i-1}+ans_{i+1}}{2}-b_i-\dfrac{c_{i-1}+c_{i+1}}{2}&is_i=0 \end{cases} \]

只需满足对于 \(is_i=0\) 的 \(i\) 有 \(c_i-\dfrac{c_{i-1}+c_{i+1}}{2}=b_i\) 即可。

于是令 \(c_1=c_2=0\) 之后递推即可。

[AGC044F] Name-Preserving Clubs \(\star\)

魔怔题。

先考虑不存在成员相同俱乐部的情况，让我们首先求出 \(k\)。

我们称一个 \(n\times m\) 的 \(\texttt{01}\) 矩阵是好的，当且仅当：不存在两行相同；任意排列它的行和列，不能得到原矩阵。

对一个 \(m\)，最小的好的矩阵对应的 \(n\) 即是我们要求的 \(k\)。

现给出几个显然的结论：

若存在一个 \(n\times m\) 的好矩阵，那么：

存在一个 \(m\times n\) 的好矩阵；
存在一个 \(n\times (2^n-m)\) 的好矩阵。

记 \(c(n,k)\) 表示好 \(n\times k\) 矩阵的数量，我们也有：

\(c(n,k)=c(k,n)=c(2^k-n,k)\)

令 \(g(n)\) 表示 \(k\) 对应的最小 \(n\)。

由结论知 \(2^{g(n)}-n \geqslant g(g(n))\)。

令 \(G(n)\) 表示满足上述条件的最小函数。

我们给出结论：

\(G(n)=g(n)\)，一个好的 \(k \times n\) 矩阵存在等价于 \(k\in[g(n),2^n-g(n)]\)。

归纳证明。

首先对于 \(n\)，我们只需证明对于 \(k\in[g(n),2^{n-1}]\) 都存在好矩阵。

对于 \(k\in[g(n),n)\)，等价于存在一个 \(n\times k\) 的好矩阵，根据归纳成立。

对于 \(k\in[n,2^{n-1}]\)，我们以如下方式构造一个 \(k \times n\) 的矩阵：

对于前 \(n-1\) 行，把第 \(\{\{1\},\{1,2\},\{2,3\},\cdots,\{n-2,n-1\}\}\) 列的位置涂黑。

对于其他的行，我们至少涂黑三个列，但是保证不与其它行重复。易证至少能有 \(2^{n-1}\) 个可区分的不同列。

接下来，我们关注如何计算 \(c(g(n),n)\)。

事实上，对于满足 \(6 \leqslant k=g(n) \leqslant n \leqslant 2^{n-1}\)，我们都有 \(c(k,n)>10^3\)。

我们考虑如下的两个 \(n\times k\) 矩阵，第一个矩阵的前 \(k-2\) 行形如 \(\{\{1,2\},\{2,3\},\cdots,\{k-2,k-1\}\\}\)，第二个矩阵的前 \(k-1\) 行如第一个矩阵取反。

接下来的 \(n-k+2\) 行，只需被涂黑的列数不是 \(2/n-2\) 即可，所以方案数至少有 \(2\binom{2^k-2\binom{k}{2}}{n-k+2}\) 种。

所以 \(c(6,6)\geqslant 2\binom{34}{2}=1122>1000\)。

对于 \(n \leqslant 5\) 的情况暴力计算。

考虑如果有相同的俱乐部，假设有 \(h\) 个不同的俱乐部，我们有成员数不多于 \(2^h\)。

因此在有相同俱乐部时，设共有 \(k\) 个俱乐部，有 \(2^{k-1} \geqslant n\)，实际上经过验证 \(g(n)\) 约为 \(\log_2 n\) 级别，有 \(k \geqslant g(n)\)。

我们可以断定 \(g(n)\) 也是在俱乐部可以相同情况下的最小答案。

计算方案，如果 \(k=g(n)\)，有 \(2^{g(n)-1} \geqslant n\)，此时当且仅当 \(n=4/7/8\) 答案才可能不大于 \(1000\)，手玩出来。

[AGC045B] 01 Unbalanced \(\star\)

Difficulty: \(\color{red}{2873}\)

考虑 dp ，记录下当前的后缀最大 \(0-1\) 值和 \(1-0\) 值。

容易发现 dp 的过程相当于在网格图上行走。

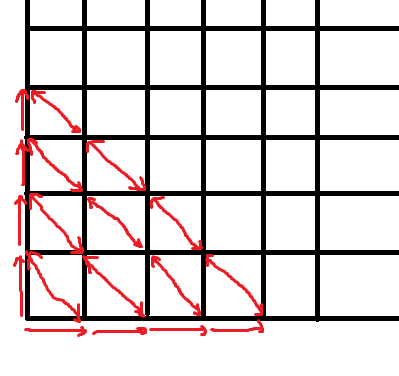
你需要走到的最远点离原点的切比雪夫距离最近。

二分答案，容易发现从原点出发相当于从对角线的任意一点出发。

维护一个可行区间，对于 \(0\) 向左移， \(1\) 向右移， \(?\) 左右取并即可。

[AGC045C] Range Set \(\star\)

Difficulty: \(\color{orange}{2758}\)

感觉比较困难的题。

依然可以套路的考虑如何构造一个指定的序列。

首先可以发现 \(0/1\) 相互对，因为容易染成全 \(0/1\) 。

设 \(a>b\) ，那么如果某个时刻出现了长度 \(\geqslant a\) 的 \(0\) 子串就一定能到达，证明显然。

那么对于一个序列，贪心把所有长度 \(\geqslant b\) 的 \(1\) 串染成 \(0\) ，判断上面的条件是否成立即可。

容斥后容易使用 \(dp\) 计数，转移比较复杂。

[AGC045D] Lamps and Buttons \(\star\)

Difficulty: \(\color{gray}{3625}\)

首先每个灯向它控制的灯连一条边。

考虑 \(m=1\) ，那么容易发现如果形成了大小为 \(n\) 的环就可行，否则不行。

进一步考虑 \(m\) 更大的情况：

我们枚举 \([1,m]\) 第一个满足 \(p_i=i\) 的位置，记为 \(x\) 。

然后就需要 \([1,x)\) 都不满足 \(p_i=i\) 而且每个环里面都有至少一个 \([1,m]\) 的元素。

考虑先一步容斥掉 \([1,x)\) 之间满足条件的点个数来消除第一个条件，接下来题目相当于：

有一张图，你需要依次加入 \(x+y+z\) 个点。

每次加入点可以插入一个自环或者插在某条边中间。

然后中间的 \(y\) 个点插入时不能是自环。

前 \(x\) 个点对应 \([1,x)\) ，中间的 \(y\) 个点相当于 \((m,n]\) ，然后最后 \(z\) 个点就对应了 \((y,m]\) 这些点。

注意容斥选定的点时不能计入 \(x,y,z\) 三个集合中。

这样得到的贡献就是：

\[x!\ \times\ \dfrac{(x+y-1)!}{(x-1)!}\ \times \dfrac{(x+y+z)!}{(x+y)!} \]

于是只需要枚举 \(x\) 和 \([1,x)\) ，复杂度 \(O(n^2)\) 。

[AGC046D] Secret Passage \(\star\)

Difficulty: \(\color{red}{2911}\)

重做一遍没想到又有点想法了。

套路的考虑两个串是有 \(S \rightarrow T\)。

把串翻转过来，操作变成删掉最后两个位置然后往中间随便插。

那么每次用 \(T\) 贪心匹配 \(S\)，如果不匹配就是操作得到的。

现在考虑一段后缀 \(P\) 能不能做出 \(a\) 个 \(0\) 和 \(b\) 个 \(1\)，\(dp\) 出来这个东西。

贪心匹配完 \(T\)，接下来只要求 \(S\) 的某个后缀满足上面的条件就行了。

记 \(dp_{i,x,y}\) 表示匹配到 \(i\) 位，现在需要 \(x\) 个 \(0\) 和 \(y\) 个 \(1\) 的 \(T\) 串方案数。

匹配上某个数字以后，考虑是否合法就行了。

[AGC047D] Twin Binary Trees

Difficulty: \(\color{red}{2910}\)

最近处理了一些二进制的题，感觉有些收获。

虽然虽然还是不会做这题。

虽然虽然这是个虚树板子。

[AGC047E] Product Simulation

Difficulty: \(\color{red}{2979}\)

少见的造计算机题。

容易得到 01 变量的乘法。

考虑如何提取 \(X\) 的 \(2^k\) 位。

从高向低枚举贪心加入 \(2^k\) 即可。

分开计算乘法加起来即可通过。

[AGC048D] Pocky game \(\star\)

Difficulty: \(\color{red}{3046}\)

感觉挺好玩的博弈论。

不妨记 \(f_{l,r,k}\) 表示区间 \([l,r]\) 中，最左边的位置只剩下 \(k\) 个球，此时先手是否必胜，类似记 \(g_{l,r,k}\) 表示最右边只有 \(k\) 个，那么转移是简单的。

容易发现 \(f,g\) 都是关于 \(k\) 单调的，所以记录下变化的位置再转移就好了。

[AGC048E] Strange Relation \(\star\)

Difficulty: \(\color{gray}{3819}\)

易知对于任意合法的 \(w\) 前缀，都可以构造出合法的剩余部分。因此可以贪心的确定 \(w\)。

考虑每个位置的贡献。

因为一个位置的 \(w\) 和之前每个 \(a/w\) 都有关，朴素的方法是枚举之前的值然后依次往后推，我们现在想独立的计算贡献。

尝试倒过来，每次在最前面插入一个元素，考虑如何调整之后的 \(w\)。

首先能 +1 的一定 +1，易知此时的 \(b\) 仍合法，而且还满足字典序最大。

dp 即可，枚举每个位置产生的贡献。

[AGC048F] 01 Record \(\star\)

Difficulrt: \(\color{blue}{\texttt{?}}\)

[The solution is deleted]

[AGC049D] Convex Sequence

Difficulty: \(\color{orange}{2602}\)

首先列出题目的式子，然后化简一下，容易发现本质上是背包，然后发现只有根号个物品有意义，于是就做完了。

注意细节。

\(O(n\sqrt{n})\).

[AGC049E] Increment Decrement \(\star\)

Difficulty: \(\color{brown}{3496}\)

倒过来，现在你需要把某个数组变成 \(0\)。

可以钦定先做了几次 \(1\) 操作，再做几次 \(2\) 操作。

我们分别研究这两种操作的影响。

首先假设对 \(a\) 序列施以 \(1\) 操作成为了 \(b\)，你需要做若干 \(2\) 操作全变为 \(0\)。

\(1\) 操作的贡献显然是 \(\sum_{i=1}^n |a_i-b_i|\)，考虑 \(2\) 操作的贡献。

可以发现 \(2\) 操作的贡献是 \(C\sum_{i=1}^n \max(0,b_i-b_{i-1})\)。

现在考虑一个朴素的 dp。记 \(dp_{i,j}\) 表示在位置 \(i\) 填上数字 \(j\) 的最小代价。

考虑转移的过程，把 dp 值画作一条折线，容易发现这是凸的。那么转移就是把斜率大于 \(C\) 的变成 \(C\)，然后加一个 \(|a_i-x|\) 的函数。

斜率显然为整数，因此在做完第一步后，斜率只有 \(C\) 种。

我们维护 \(C\) 个斜率变化的位置，然后每次相当于插入两个 \(a_i\)，然后删掉最小和最大的元素。

我们考察 \(dp_{i,0}\) 的值，可以发现值就是之前基础上加上 \(a_i\) 减去最小值。

md编不下去了，这题怎么这么难

[AGC050D] Shopping

Difficulty: \(\color{orange}{2674}\)

枚举第 \(x\) 个人的答案，然后就大力dp，记 \(dp_{i,j,k}\) 表示 dp 目前到第 \(i\) 个人，然后 \(j\) 个前面的人没拿到，\(k\) 个后面的没拿到，随便走走就 \(O(n^6)\) 了。

考虑一次转移 \([1,x-1],[x+1,n]\) 的人的答案。

枚举前面有多少人拿到了，预处理出有 \(x\) 个礼物，\(y\) 个人拿，有 \(z\) 个人拿到的概率记为 \(f_{x,y,z}\)，应该就能直接转移了。

以上是口胡，实现🕊了。

[AGC051D] C4 \(\star\)

Difficulty: \(\color{red}{2807}\)

感觉好强的一个题，虽然事实上这个题列出式子就 win 了，但是大量的观察和一定的勇气是必不可少的。

首先考虑利用环长为 \(4\) 的性质，注意到一步一步考虑比较困难，我们同时考虑相邻的两步，那么此时操作的形式就非常简单了：

\(1\rightarrow3 , 3\rightarrow1 , x\rightarrow x\) 。

注意到有 \(1,2\) 操作数量相等，枚举使用的次数记为 \(k\)，此时我们知道 \(3\) 操作的使用次数了。

在 \(1\) 上原地不动的次数是 \(\dfrac{a+d-2k}{2}\)，\(3\) 上原地不动的次数是 \(\dfrac{b+c-2k}{2}\)。

不妨枚举使用了 \(x\) 次 \(1-2-3\)，也就是 \(2k-x\) 次 \(1-3-4\)。

此时我们有 \(1-2\) 上的边还有 \(a-x\) 次，类似的可以推出其他边的次数。

那么就可以列出式子计算了，容易发现答案等于：

\[\sum_{k,x}\binom{2k}{x}\binom{\frac{a+d-2k}{2}}{\frac{a-x}{2}}\binom{\frac{b+c-2k}{2}}{\frac{b-x}{2}}\binom{\frac{a+d-2k}{2}+k}{k}\binom{\frac{b+c-2k}{2}+k-1}{k-1} \]

式子的分别含义是：选择一二操作的方向；组合 \(1,3\) 号点的原地不动；把三操作插入一二操作。

勇敢的你把它拆开得到：

\[\sum_{k,x}\dfrac{(2k)!\frac{a+d-2k}{2}!\frac{b+c-2k}{2}!\frac{a+d}{2}!\frac{b+c-2}{2}!}{x!(2k-x)!\frac{a-x}{2}!\frac{d+x-2k}{2}!\frac{b-x}{2}!\frac{c+x-2k}{2}!\frac{a+d-2k}{2}!k!\frac{b+c-2k}{2}!(k-1)!} \]

\[=\sum_{k,x}\dfrac{(2k)!\frac{a+d}{2}!\frac{b+c-2}{2}!}{x!(2k-x)!\frac{a-x}{2}!\frac{d+x-2k}{2}!\frac{b-x}{2}!k!\frac{c+x-2k}{2}!(k-1)!} \]

容易发现本质上是卷积，于是可以做到 \(O(n\log n)\)。

[AGC052D] Equal LIS \(\bigstar\)

Difficulty: \(\color{brown}{3304}\)

比较好玩的一个题。

记 \(f(x)\) 表示以 \(x\) 结尾的 \(\text{LIS}\) 最大长度。

考虑如果原序列的 \(\text{LIS}=2k\)，那么只要按照是否有 \(f(x)\leqslant k\) 分成两类即可。

否则令 \(\text{LIS}=2k+1\)，此时我们尝试能否把原序列分成两份，每份的 \(\text{LIS}\) 长度是 \(k+1\)。

容易发现，只要原序列中存在一个元素，它不在被选出的某个最长 \(\text{LIS}\) 中，且存在一个长度为 \(k+1\) 的上升子序列包括它，那么就能构造。

记一个满足如上条件的元素为 \(a_x\)，包含 \(a_x\) 的一个上升子序列为 \(a_{p_1},\cdots,a_{p_{k+1}}\)。我们按如下的方式分配：

首先我们把个长度为 \(k+1\) 的上升子序列全选入第一个序列。

对于某个其他的元素 \(y\)，如果满足 \(f(y)\not=f(a_{p_i})\)，我们就把它选入第二个序列。否则如果 \(f(y)=f(a_x)\)，我们也把它放进第二个序列。其他的情况我们就把它放进第一个序列。

考虑第一个序列，显然存在长度为 \(k+1\) 的上升子序列，然而只存在 \(k+1\) 种不同的 \(f\)，因此其 \(\text{LIS}\) 为 \(k+1\)。

同理可以知道第二个序列的 \(\text{LIS}\) 也为 \(k+1\)。

如果不存在这样的 \(a_x\)，则显然无解。

[AGC052E] 3 Letters \(\star\)

Difficulty: \(\color{brown}{3457}\)

看上去很典而有点难度的题。

显然把一个位置变成相对的 \(\pm 1\)。

我们可以计算出在这个意义下的前缀和，记为 \(a\)。同样计算答案的前缀和记为 \(b\)。

那么在这个前缀和的意义下，一次操作就是把某个位置 \(\pm 2\)，而且要求相邻两项的差的绝对值为 \(1\)。

可以发现此时的最小操作次数为 \(\dfrac{\sum |a_i-b_i|}{2}\)，而且显然可以达到。

我们只需要合理的调控 \(a,b\) 的初始值使得这个答案最小。

经典的选择中位数即可。

[AGC053D] Everyone is a winner \(\bigstar\)

Difficulty: \(\color{gray}{3949}\)

非常神秘的题。

显然，如果我们决策了第 \(i\) 个人前 \(i\) 步做哪些题，那么前 \(i\) 步和后 \(n-i\) 步分别是按花费时间从大至小做题。

从后往前考虑每个人，为了让前面人的选择空间更加大，我们首先最大化其做完第 \(i\) 题的时间，其次要尽量选 \(3\)。

记 \(t_{i,j}\) 表示第 \(i\) 个人做完第 \(j\) 题的所需时间，\(T_j\) 表示目前的限制。初始 \(T_j\) 为每个人按时间倒序做题时最短时间。

接下来考虑到第 \(x\) 个人时，对 \(1\leqslant y <x\) 更新 \(T_y=\min(T_y,t_{x,y})\)。

显然这样能让前面的人的选择空间尽可能多，唯一的问题是是否会让后面的人不是最快。

我们声称，在时间消耗是 \(\{1,2,3\}\) 的情况下，不会出现这种问题。即我们有：\(T_x\leqslant t_{y,x}\)。

考虑证明，如果我们在考虑第 \(i\) 个人时有 \(T_i +2 \geqslant T_{i+1}\)，则显然对 \(j>i\) 有 \(T_i+2(j-i)\geqslant T_j\)。

也就是说，只要 \(i+1\) 不是全用 \(3\) 填前一半，那么 \(i\) 后面填的一串 \(2,3\) 都一定是合法的，另外 \(T\) 的初始值也确保了后面填 \(i\) 的部分合法。至于 \(i+1\) 用 \(3\) 填前一半的情况，也易于经过讨论证明合法。

用一个斜率为 \(1/2/3\) 的凸包维护 \(T\) 即可。时间复杂度 \(O(n)\)。

[AGC053E] More Peaks More Fun \(\star\)

Difficulty: \(\color{gold}{4036}\)

考试题。

不妨令同一组有 \(b_i > a_i\)，我们将它任意排列后，合法当且仅当：

1. \(\forall k, b_k>a_{k+1}\)
2. \(\exist p<n,\forall k<p,b_k>a_{k+1};b_p < a_{p+1};\forall k>p,b_k>a_{k-1}\)

例如，对于 \((1,5),(2,6),(3,4)\) 这种排列法，就满足 \(\text{\#1}\)。

对 \((1,3)(5,4)(6,2)\) 这种排列法，就满足 \(\text{\#2}\) 且有 \(p=1\)。

不难发现这两组条件包括了所有满足条件的序列，我们只需转而计数这两种方案的贡献。

从较为简单的第一种入手，我们将二元组对 \(b\) 排序，那么接下来考虑构造的方式。

我们倒着依次插入二元组，因为插入到一个位置时一定满足前面的条件，所以我们只需令后面的条件满足，即每个位置 \(i\) 的贡献为 \(1+\sum_{k>i,b_i>a_k}1\)，记为 \(1+w_i\)。

现在考虑第二种，我们能枚举 \(p\) 和 \(p+1\) 所对应的二元组 \(x,y\)，那么有 \(x < y\)，可以转化为分别构造出两个以 \(x,y\) 结尾的数组，每一个数组都满足上面的条件，然后倒过来一个再拼接。

于是现在我们来讨论每一段的贡献：

1. \(i>y\)，此时和上面是类似的，而且都可以插入至 \(x,y\) 的前面，那么贡献为 \(2+w_i\)。

2. \(i \in (x,y)\)，此时 \(y\) 的贡献已经被统计，且无论如何都能插入 \(x\) 的前面，贡献为 \(1+w_i\).

3. \(i<x\)，类似，贡献为 \(w_i\)。

这样就能做到 \(O(n\log n)\) 了。

[AGC053F] ESPers \(\star\)

Difficulty: \(\color{blue}{\texttt{?}}\)

转化题意：

容易发现，设 \(t\) 时刻是最后一个时刻，使得 \(A/B\) 投票数量相等。

在 \(t\) 时刻前投票的超能力者有 \(0.5\) 的概率 win，\(t\) 时刻后投票的超能力者一定 win。

于是只需计数前 \(t\) 时刻投票的超能力者数目。

我们用另外一个序列来帮助我们计数。

考虑序列 \(a\)，如果第 \(i\) 个投票的投给了多数，\(a_i\) 就为 \(1\)，否则为 \(-1\)。（如果二者票数一样，如果投票者不是超能力者则有一半概率为 \(1\)）

那么一个合法的 \(a\) 序列形如：

\[S_0,-1,S_1,-1,\cdots,-1,S_x,1,S_{x+1},1,\cdots,1,S_{x+y} \]

其中 \(S\) 是一个串，满足最长的前提下，每个前缀和都非负，且和为 \(0\)。而且与原 \(a\) 序列相比显然唯一。

接下来我们需要计算：

1. \(x,y\) 的选择方案。
2. 选出超能力者。
3. 前 \(t\) 时刻投票的超能力者数目。
4. 得到原串的概率。
5. 从原串得到 \(a\) 序列的概率。

考虑到超能力者只可能对应 \(1\)，考虑这个序列中 \(1\) 的出现次数。

容易发现出现了 \(w=\dfrac{2n+1-x+y}{2}\) 个 \(1\)。

所以选超能力者的方案数是 \(\binom{w}{k}\)。

另外，考虑每个非超能力者的贡献。

如果一个非超能力者投票时，票数不同则为得到原串的概率贡献 \(1/2\)，否则为得到 \(a\) 序列的概率贡献 \(1/2\)，因此这部分的贡献是：\(\dfrac{1}{2^{2n+1-k}}\)。

接下来考虑 \(t\) 的取值。

容易发现，在 \(S_x\) 之前，每两个 \(-1\) 两边就平票了。

经过仔细分析，可以发现：

如果 \(x\) 是偶数，那么 \(t\) 就是 \(S_x\) 的结尾。
否则，\(t\) 是 \(S_{x-1}\) 的结尾。

而它们中出现 \(1\) 的期望数量就是：

\(\dfrac{(x+1)(2n+1-x-y)}{(x+y+1)}\) 或者 \(\dfrac{x(2n+1-x-y)}{(x+y+1)}\)。

而总 \(1\) 个数为 \(2n+1-x+y\)，因此贡献为：

\(\dfrac{(x+1)(2n+1-x-y)}{(x+y+1)(2n+1-x+y)}\) 或者 \(\dfrac{x(2n+1-x-y)}{(x+y+1)(2n+1-x+y)}\)。

我们还需要考虑最后一项，即 \(S\) 的选择方案数。

\(S\) 是有强大的组合意义的，在两项 \(S\) 中插入一个 \(1\)，易证方案数为从 \((0,0)\) 走斜线到 \((2n+1,x+y)\) 的方案数。

即 \(\Large{\binom{2n+1}{\frac{2n+1-x-y}{2}}-\binom{2n+1}{\frac{2n-1-x-y}{2}}}\)。

综合起来，由于为每个原串分配超能力者的概率为 \(\dfrac{1}{\binom{2n+1}{k}}\)，把前面全部乘起来得到：

\[\text{let } w=\dfrac{x+y-1}{2}:\\ \]

\[Ans=\sum_{x,y}\dfrac{(2n+1-x-y)\binom{\frac{2n+1-x+y}{2}}{k}}{(2n+1-x+y)\binom{2n+1}{k}2^{2n+1-k}} (\binom{2n+1}{n-w}-\binom{2n+1}{n-w-1}) \times \begin{cases} \frac{x}{x+y+1}&x 是奇数\\ \frac{x+1}{x+y+1}&x 是偶数 \end{cases} \]

我们只需枚举 \(x,y\) 即可得到答案。

整理上式，其实我们只需求：

\[\dfrac{1}{\binom{2n+1}{k}2^{2n+1-k}}\sum_{x=2t+1,y}\dfrac{x(n-w)\binom{\frac{2n+1-x+y}{2}}{k}}{(w+1)(2n+1-x+y)} (\binom{2n+1}{n-w}-\binom{2n+1}{n-w-1}) \]

为了方便，只讨论 \(x\) 为奇数的情况。

我们有 \(y=2w+1-x\)，带入得：

\[\dfrac{1}{\binom{2n+1}{k}2^{2n+1-k}}\sum_{w}\dfrac{x(n-w)\binom{n+w-x+1}{k}}{(w+1)(2n+2w-2x+2)}(\binom{2n+1}{n-w}-\binom{2n+1}{n-w-1}) \]

\[=\dfrac{1}{\binom{2n+1}{k}2^{2n+1-k}}\sum_{w}\dfrac{(n-w)}{(w+1)}(\binom{2n+1}{n-w}-\binom{2n+1}{n-w-1})\sum_{x=2t+1\leqslant 2w+1}\dfrac{x\binom{n+w-x+1}{k}}{2(n+w-x+1)} \]

对后面一坨吸收，可以预处理后 \(O(1)\) 计算，因此总复杂度 \(O(n)\)，可以通过此题。

整理一下，我们需要对后面这部分预处理：

\(\sum_{x=2t\leqslant 2w+1}\dfrac{x\binom{n+w-x+1}{k}}{2(n+w-x+1)}=\dfrac{1}{2k}\sum_{x=2t+1\leqslant 2w+1}x\binom{n+w-x}{k-1}\)

在 \(k\) 固定时，我们维护：

\(S1_n=\sum\limits_{i=2t+1}^n \binom{i}{k-1}\)
\(S2_n=\sum\limits_{i=2t+1}^n i\binom{i}{k-1}\)

然后就有 \(\sum_{x=2t+1\leqslant 2w+1}x\binom{n+w-x}{k-1}=(n+w)(S1_{n+w-1}-S1_{n-w-3})-(S2_{n+w-1}-S2_{n-w-3})\)。

同样处理偶数情况。

[AGC054D] (ox) \(\star\)

Difficulty: \(\color{brown}{3426}\)

不会做，感谢 \(xzy\) 的指导。

先考虑只有 \(\texttt{()}\) 的情况，这是一个简单的贪心。

结论：
存在一个最优解，删掉所有的 \(\texttt{o/x}\) 后得到的串与最初串删掉 \(\texttt{o/x}\) 后的最优解相同。

不知道怎么证，下次补。

那么直接 \(dp\) 就行了。

[AGC054E] ZigZag Break \(\star\)

Difficulty: \(\color{brown}{3499}\)

[AGC055D] ABC Ultimatum \(\bigstar\)

Difficulty: \(\color{brown}{3506}\)

牛逼的。

怎么想到的呢？不知道。
怎么出出来的呢？不知道。

证明显然，但是怎么考虑出一种直观的理解呢？

[AGC055E] Set Merging \(\bigstar\)

Difficulty: \(\color{blue}{\texttt{?}}\)

据说 anton 找性质从来不用草稿纸/电脑，全在脑子里想，不知道是不是真的。

考察某个时刻的 \(L_i,R_i\) 满足何种性质。

考察一次对 \((i,i+1)\) 的操作，可以发现就相当于令：

\[L_{i+1} \rightarrow L_i\\ R_i \rightarrow R_{i+1} \]

现给出结论：

结论：定义排列 \(P\) 初始满足 \(P_i=i\)，每次操作 \((i,i+1)\) 后交换 \(P_i,P_{i+1}\)。则 \(S_i=[\min_{j\geqslant i}P_j,\max{j\leqslant i}P_j]\)。

证明🕊了，其实随便考虑一下就是对的。

于是你分析一下就可以知道每个位置的 \(P\)，答案显然是最小逆序对数，贪心即可。

官方题解的 Bouns 里写可以线性，有知道的老哥可以讲解一下吗/kel

[AGC056E] Cheese \(\bigstar\)

Difficulty: \(\color{gray}{3877}\)

比较新颖的题。

首先有一个比较显然的观察：我们调换不同位置放奶酪的时间，不会改变答案。记第 \(i\) 个间隔放了共 \(c_i\) 个奶酪。

概率显然为 \((n-1)!\prod_i \dfrac{a_i^{c_i}}{100^{c_i}c_i!}\)。

同样的，我们不用考虑每个奶酪何时停下，只需知道有多少奶酪经过了某个老鼠，即可算出这个老鼠的概率。

感性的，因为我们可以随意分配奶酪的开始点和结束点，不妨令每个奶酪都不会转超过一圈。

考虑计算第 \(x\) 个人的答案，不妨令 \(x=n\)。记有 \(y\) 个奶酪经过了第 \(n\) 个人，那么显然，答案只和 \(c_i\) 以及 \(y\) 有关。

如果我们枚举 \(y\)，使用 \(dp\) 计算 \(c\) 的所有取值，就能算出这种情况下 \(n\) 恰好没吃到的概率。

具体的，记有 \(b_i\) 个奶酪经过了第 \(i\) 个老鼠，那么概率是：\(2^{-b_n}\prod_{i<n} (1-2^{-b_i})\)。

接下来只需计算出现此情况的概率，易于计算。

注意到我们可能计算到一些 “没有终点和起点” 的奶酪，而每出现一种这样的奶酪就会令概率变为 \(\dfrac{1}{2}\)，因此真正的答案就是我们算出的值除二。

由于之前所述的奶酪的存在，我们在计算答案时将其保留为 \(2^{-x}\) 的多项式，最后一次性计算贡献。

[AGC057D] Sum Avoidance \(\star\)

Difficulty: \(\color{brown}{3307}\)

相当的阴间题。

显然答案是 \(\lfloor\dfrac{n-1}{2}\rfloor\)，选择更大一半的数字即可满足此要求。

容易发现 \(x\) 和 \(S-x\) 互斥，令 \(x \leqslant \dfrac{n}{2}\)，我们肯定想要小的数字。

一个暴力的做法是，考虑从小往大枚举每个数字，能加就加，做背包。

可以先枚举选出集合的最小的数字，记为 \(w\)。容易发现，若 \(w\) 被选择，则 \(\forall k,\ kw\) 都被选择。这个最小的数字只需满足不能被 \(x\) 整除就行了。

另外考虑到如果 \(x_1,x_2\) 被选择，那么我们也可以选 \(x_1+x_2\)。所以我们维护一个模 \(w\) 的同余类，每个类只需求出最小的能被选的数字，就能直接得到答案了。

于是每次背包都只需要做 \(O(w)\) 的位置，也只有 \(O(w)\) 个数字需要做背包，另外 \(w\) 相当小，于是直接过了。

具体的实现相当神秘。

[AGC057E] RowCol/ColRow Sort

Difficulty: \(\color{gold}{4128}\)

只能说 new AGC 的题网上要么没题解，要么两三行，整个一个阅读理解/tuu。

记 \(S\) 为 \(B\) 的最大值。

显然，对每个 \(k\) 把大于 \(k\) 的位置变成 \(1\)，不大于 \(k\) 的变成 \(0\)，如果 \(A\) 都能变成 \(B\) 就是合法的。

先考虑 \(S=1\)，由于 \(B\) 已知，记 \(r_i\) 表示 \(A\) 第 \(i\) 行的和，\(c_i\) 表示 \(A\) 第 \(i\) 列的和，那么一个 \(r\) 的可重集一定对应一个 \(c\) 的可重集。

这两个可重集构造出来和用 \(B\) 构造出来是一样的，于是我们只要分配每一行/列对应多少。

记排列 \(p,q\) 表示把每行/列排序后，每行对应 \(1\) 的数量是第几小，容易转化为只需求合法的 \(p,q\) 数量。此时 \(p,q\) 是没有任何限制的。

此时 \(A_{i,j} = 1\) 等价于 \(B_{p(i),q(j)}=1\)。

考虑 \(S\not=1\) 的情况，从大到小考虑 \(k\)，对不同的 \(k\) 重新定义 \(p_k,q_k\)。

这个过程相当于每次只能选出一些就原来是 \(1\) 的挪到下一层仍为 \(1\)。

也就是必须满足：

\(B_{p_k(i),q_k(j)}\leqslant k \rightarrow B_{p_{k+1}(i),q_{k+1}(j)}\leqslant k+1\)

感性理解，由于 \(p_k,q_k\) 没有其他限制，我们总可以构造一个合理的双射把条件变成这样：

\(B_{i,j}\leqslant k \rightarrow B_{p_k(i),q_k(j)}\leqslant k+1\)

即各层独立。

记 \(a_i=\sum_j [B_{i,j} \leqslant k]\)，\(b_j=\sum_i [A_{i,j} \leqslant k+1]\)。

通过上面，我们能知道对每个 \(x\in[1,a_i]\) 我们都有 \(B_{i,x}\leqslant k\) 也就是 \(B_{p_k(i),q_k(x)}\leqslant k+1\)。

因为有 \(b_{q_k(x)} \geqslant p_k(i)\)，然而 \(b\) 不增，于是 \(b_{\max\{q_k(x)\}} \geqslant p_k(i)\)，其中 \(x\in[1,a_i]\)。

把 \(a_i\) 排好序，直接 dp 即可。

[AGC058E] Nearer Permutation \(\bigstar\)

Difficulty: \(\color{gray}{3825}\)

显然首先考虑如何对排列 \(p\) 计算 \(F(p)\)。

记 \(w\) 为 \(p\) 中逆序对数目一半下取整。

维护一个一开始为 \(p\) 的数组 \(a\)，接下来每次从 \(a_1,\cdots,a_{w+1}\) 中选出最小 \(a_i\) 的插到序列 \(q\) 的末尾，然后令 \(w \to w-i+1\)。

现在来考察 \(y=F(x)\) 有什么性质。记 \(k\) 为第一个满足 \(y_k > y_{k+1}\) 的位置。

实际上，我们可以求出 \(x\) 的逆序对数。

手动模拟一下，会发现：

在 \(y_{k}\) 被删除前，一定在 \(x\) 里是当时最靠前的位置；\(y_{k}\) 被删除以后，\(y_{k+1}\) 恰好进入了被删除的范围；删掉 \(y_{k+1}\) 后，剩下的原序列 \(x\) 就是 \(y_{k+2},y_{k+3},\cdots\)。

现在尝试逆推，显然 \(y_k,y_{k+2},y_{k+3},\cdots\) 就是 \(x\) 的最后几项。

接下来，我们需要对每个 \(i=k+1,k-1,k-2,\codts,1\)，把 \(y_i\) 向后移动到某个合适的位置来得到 \(x\)。

记 \(c_i\) 表示 \(y_i\) 向后移动的长度，我们只需得到每个 \(c_i\) 即可解决这个问题。令 \(p\) 表示 \(y_{k+1}\) 的位置。考虑 \(v=w-p\) 的值。

事实上，经过讨论我们知道：令任意一个 \(c_i \to c_i+1\) 均会使 \(v\) 减少 \(\dfrac{1}{2}\)。

因为经过前面的分析我们知道最后 \(v\) 是 \(0\) 或 \(\dfrac{1}{2}\)，最初是 \(\dfrac{inv}{2}\)（\(inv\) 是逆序对数），于是就能通过 \(\sigma s\) 知道 \(inv\)。

贪心把 \(y_i\) 往后移即可。

---

---

以下是 ARC 部分。

[ARC089D] ColoringBalls \(\star\)

Difficulty: \(\color{gray}{3782}\)

好像做多了这种序列题确实能提升自己这方面的能力。

仍然是套路的考虑怎么用一个操作序列构造出一个特定的颜色序列。

首先把相邻的蓝色/红色并到一起，然后对于每一段考虑：

如果这一段是纯蓝，那么只会消耗一个 \(B\) 。

否则形如 “蓝红蓝红蓝” 这样，容易发现它会消耗类似 蓝+红+若干个任意，任意的数目就相当于红的段数-1。

于是从前往后扫一下，优先匹配蓝/红，其次匹配任意。

那么反过来解决原问题，我们需要枚举有几个蓝色段，几个混色段，然后计算答案。

注意到我们还需要选择混色段选择的顺序，那么我们钦定红色段多的混色段在前面，最后阶乘就行了。

记 \(dp_{}\) 表示放了 \(i\) 个混色段，最后的一个混色段有 \(j\) 个红色段，总共消耗长度为 \(k\) 的答案，每次转移一些红色段数目相同的混色段，那么只需要枚举红色段数目和总长度，预处理一下即可做到 \(O(n^5)\) 。

[ARC117F] Gateau \(\star\)

Difficulty: \(\color{brown}{3378}\)

写个套路做法。

首先容易想到二分答案，然后转成差分约束。

即计前缀和为 \(s\) ，对于每一个 \(s_{i+n}-s_i\) 都有一个上下界，然后要求 \(s\) 单调不降。

图建出来大概是这样子：

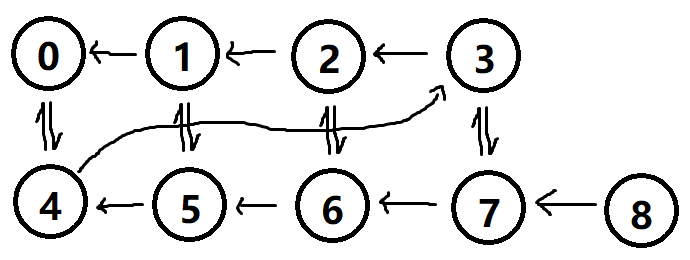
现在删掉边 \(n\rightarrow n-1\) 和 \(0 \rightarrow n\) ，把剩下的点配成点对如 \((1,5),(2,6),(3,7)\) ，然后对于在同一个点对的点一起更新最短路，容易发现可以 \(O(n)\) 计算。

最后再加入那个被删掉的边，此时有意义的点非常少。随便做做就行了。

[ARC122F] Domination \(\bigstar\)

Difficulty: \(\color{blue}{\texttt{?}}\)

首先发现这种看起来就神仙的题，大多数时候需要使用图论算法。

考虑 \(k=1\) ，那么每个红色只需要匹配一个蓝色即可。

容易发现只有一个斜向的红色点集是有用的。找出来，然后按 \(x\) 排序。

删掉已经被满足了的红色点，然后考虑移动蓝色点。

考虑一个这样的建图方式：

我们考虑一个蓝色点向上移动满足一个红色点的消耗是它们的 \(x\) 之差，而且一次可以满足一段这样的点，向右移动同理。

那么以这种方式建图：

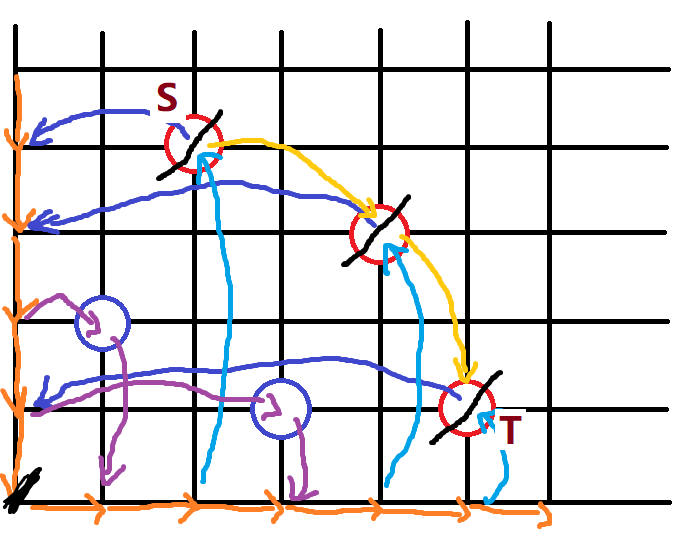
（每种不同的边都上好了色，注意途中只有橙色边的边权为 \(1\) ，橙色边还有边权为 \(0\) 的逆向边。）

考虑从一个红点 \(L\) 跑到另外一个红点 \(R\) ，经过了蓝点 \(x\) 即代表用 \(x\) 满足 \([L,R]\) 。

因此答案即 \(S \rightarrow T\) 的最短路。

对于 \(k \not = 1\) ，根据经典结论，可以拆成 \(k\) 个 \(k=1\) 的子问题，因此上个费用流就行了。

题目好 nb ！我好菜/ll

[ARC132E] Paw \(\star\)

Difficulty: \(\color{red}{3144}\)

有难度的计数题。

首先有一个结论：最后的形态形如 <<<<___>>>> ，其中 _ 是不变化的部分。

因此简化为只需给一边排列顺序并选择方向，使得满足最后变成 <<<< 。

记 \(d_i\) 为 \(i\) 个 \(.\) 的答案，那么在左侧插入一个 \(.\) ，它的选择方案有 \(2i+1\) 种，即：

\[d_{i+1}=(2i+1)d_i \]

直接计算即可。

[AGC140F] ABS Permutation (Count ver.) \(\star\)

Difficulty: \(\color{brown}{3392}\)

生成函数基础练习（bushi

考虑使用生成函数解决问题。

首先二项式定理，只需求钦定有 \(k\) 个位置满足条件的方案。

容易抽象成有 \(w\) 条长度为 \(l\) 的链，你可以随意钦定一条边是否满足条件，最后需要把若干个边组成的链拼起来。

首先我们考虑一条链的生成函数，记元 \(x\) 表示点数，\(y\) 表示边数，考虑到只要点数大于等于 \(2\) 就可以选择 reverse，所以生成函数形如：

\[F(x,y)=x+2x^2y+2x^3y^2+\cdots \]

\[=x+2x^2y\dfrac{1}{1-xy}=\dfrac{x(1+xy)}{1-xy} \]

现在你可以随意拼接链，也就是你需要求：

\[[x^l]\dfrac{1}{1-\dfrac{x(1+xy)}{1-xy}} \]

\[=[x^l]\dfrac{1-xy}{1-xy+x+x^2y} \]

\[=[x^l]\dfrac{1-xy}{1-x(y+1+xy)} \]

因为有

\[[x^m]\dfrac{1}{{1-x(y+1+xy)}} \]

\[=[x^m]\sum_i x^i(y+1+xy)^i \]

\[=\sum_i \binom{i}{m-i}y^{m-i}(y+1)^{2i-m} \]

现在需计算这个的 \([y^t]\) 项，得到：

\[[y^t]\sum_i \binom{i}{m-i}y^{m-i}(y+1)^{2i-m} \]

\[=\sum_i \binom{i}{m-i}\binom{2i-m}{t-m+i} \]

卷积计算即可。

于是现在我们得到了 \(G(x)=[x^l]F(x,y)\)，快速幂得到 \(G^w(x)\) 即可解决此问题。

[ARC142E] Pairing Wizards \(\star\)

Difficulty: \(\color{brown}{3232}\)

感觉虽然思维路径比较短，但是实际上并不非常简单。

首先对于每条边，我们让每个数都满足更小的限制，显然这是必须的。

考虑一个点，假设它连向了一个 \(b\) 大于等于它的点，我们称它是优秀的。

那么如果两个优秀的点之间有连边，那么我们显然可以忽略它。

于是优秀的点和不优秀的点之间构成了二分图，可以使用经典的网络流建模解决。