题目描述
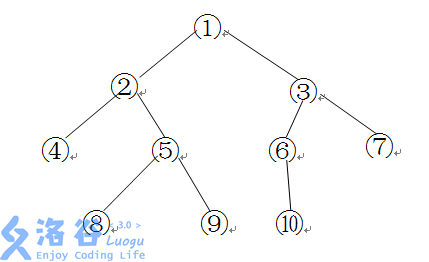
如下图所示的一棵二叉树的深度、宽度及结点间距离分别为：
深度：4 宽度：4（同一层最多结点个数）
结点间距离： ⑧→⑥为8 (3×2+2=8)
⑥→⑦为3 （1×2+1=3）
注：结点间距离的定义：由结点向根方向（上行方向）时的边数×2，
与由根向叶结点方向（下行方向）时的边数之和。
输入格式
输入文件第一行为一个整数n(1≤n≤100)，表示二叉树结点个数。接下来的n-1行，表示从结点x到结点y（约定根结点为1），最后一行两个整数u、v，表示求从结点u到结点v的距离。
输出格式
三个数，每个数占一行，依次表示给定二叉树的深度、宽度及结点u到结点v间距离。
输入输出样例
输入 #1 输出#2
10 4 1 2 4 1 3 8 2 4 2 5 3 6 3 7 5 8 5 9 6 10 8 6
解析
这道题可以分为两种情况来看：1.一个点是另一个点的祖先 2.两个点在不同的子树中，有公共祖先
按照题意，在计算结点u到结点v的距离时，求的是：u向上时所经过的边数×2+v向上时所经过的边数
先分别举两种情况的几个例子方便理解：
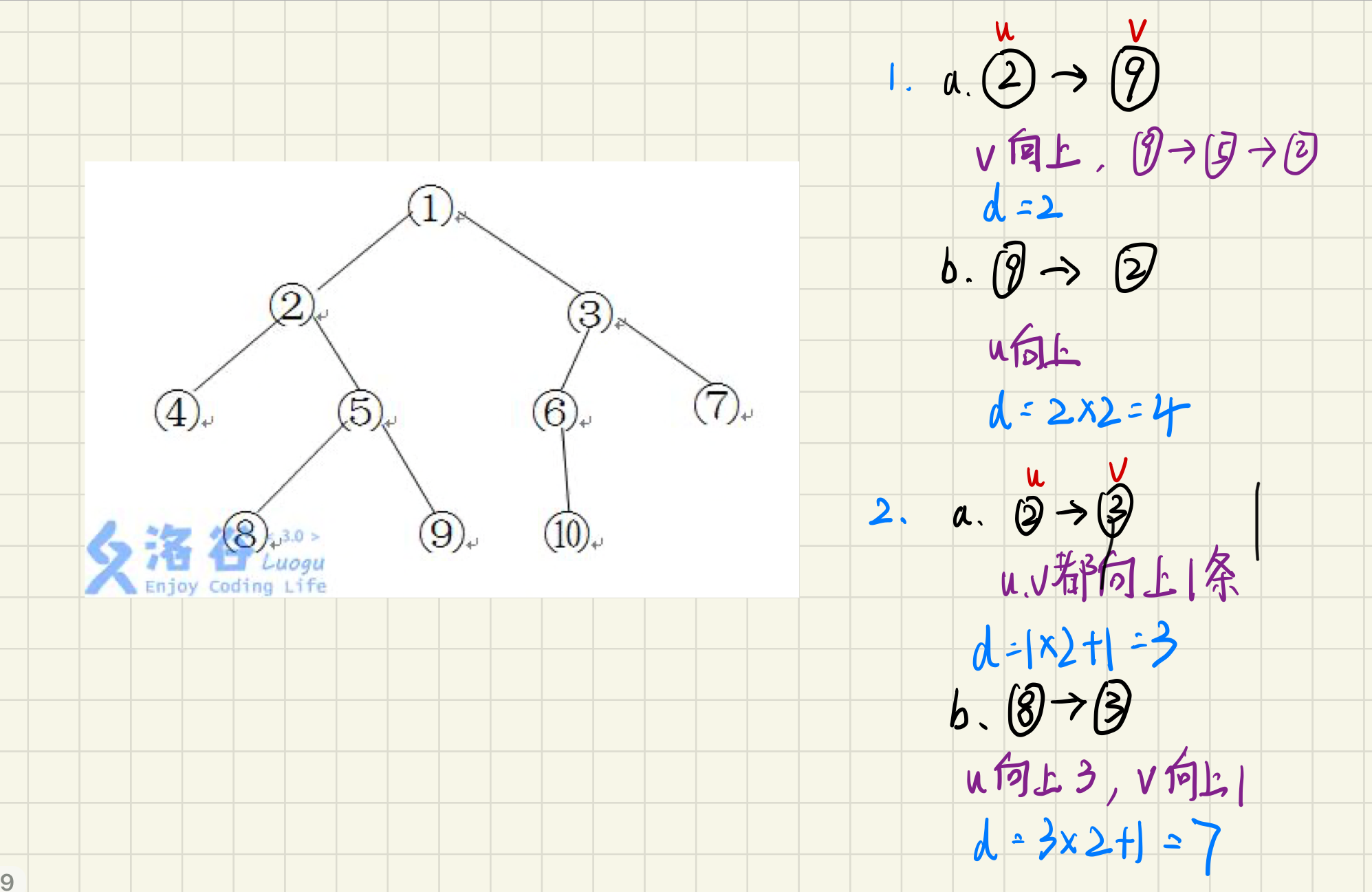
接下来我们来具体分析两种情况的写法，记u向上时为d1，v向上时为d2
1.一个点是另一个点的祖先
a.u是v的祖先（如图中的例子1.a） 这时v向上，不用×2，所以输出的是d2+1
b.v是u的祖先 （如图中的例子1.b） 这时u向上，要×2，所以输出的是（d1+1）*2
2.两个点在不同的子树中，有公共祖先
a.两点深度一样但不是一个祖先 这时u,v同时向上走
b.两点深度不同 这时可以判断两个点的深度，谁深度更大，谁往上走
关于二叉树的深度、宽度：深度就是总共有几行，宽度就是找出结点数最多的那一行，求出那一行的结点数数量
代码：
#include <iostream> using namespace std; struct tree { int deep;//每个点的深度 int zu;//这个点的根节点，即它的祖先 }t[101]; int n,d=1,w=0;//d为深度，w为宽度,注意深度初始值为1 int wid[101];//宽度，找结点数最多的那一行 int main() { cin>>n; int i,u,v; t[1].deep=1;wid[1]=1; for(i=1;i<n;i++)//注意，题目是n-1行 { cin>>u>>v; t[v].zu=u;//u是v的祖先 t[v].deep=t[u].deep+1;//v的深度是u深度加一 if(t[v].deep>d) d=t[v].deep;//找最大深度 wid[t[v].deep]++;//记录那一行的结点数 } cin>>u>>v;//输入要求距离的u,v for(i=1;i<=d;i++)//循环每一行 { if(wid[i]>w) w=wid[i];//找到结点数最多的那一行，即最大宽度 } cout<<d<<endl<<w<<endl;//输出最大深度和最大宽度 if(u==v) cout<<0;//判断特殊情况 else { int d1=0,d2=0;//d while(t[u].zu!=t[v].zu) { if(t[u].zu==v) //v是u的祖先，u向上 { cout<<(d1+1)*2; return 0; } if(t[v].zu==u)//u是v的祖先，v向上 { cout<<d2+1; return 0; } if(t[u].deep>t[v].deep)//u在v下面，u向上 { d1++; u=t[u].zu; } if(t[v].deep>t[u].deep)//v在u下面，v向上 { d2++; v=t[v].zu; } if(t[u].deep==t[v].deep&&t[u].zu!=t[v].zu)//u,v在同一层，但不是一个结点,二者同时向上 { d1++;d2++; u=t[u].zu;v=t[v].zu; } } cout<<(d1+1)*2+d2+1; } return 0; }
（参考洛谷题解而来）
