[转] 网络流算法--Ford-Fulkerson方法及其多种实现
网络流
转载自:http://www.cnblogs.com/luweiseu/archive/2012/07/14/2591573.html
在上一章中我们讨论的主题是图中顶点之间的最短路径,例如公路地图上两地点之间的最短路径,所以我们将公路地图抽象为有向带权图。本章我们将对基于有向带权图的模型做进一步扩展。
很多系统中涉及流量问题,例如公路系统中车流量,网络中的数据信息流,供油管道的油流量等。我们可以将有向图进一步理解为“流网络”(flow network),并利用这样的抽象模型求解有关流量的问题。
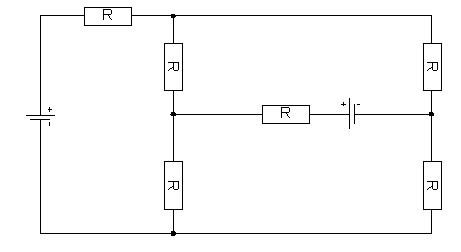
图 电路原理图可抽象为网络流
流网络中每条有向边可以认为是传输物质的管道,每个管道有固定的容量,可以看作是物质能够流经该管道的最大速度。顶点是管道之间的交叉连接点,除了汇点之外,物质只流经这些点,不会再顶点滞留或消耗。也就是说,物质进入某顶点的速度必须等于离开该顶点的速度。这一特性被称为“流守恒”(flow conservation)。例如图中的电路原理图,根据基尔霍夫电流定律,在每个交叉连接点出,流进的电流等于流出的电流。电流的定义为单位时间内通过导线某一截面的电荷量,即为电荷的流动速度。所以,用流守恒的观点可以理解为:电荷量流进某交叉顶点的速度等于离开该顶点的速度。
在本章我们将讨论最大流问题,这是流网络中最简单的问题:在不违背容量限制的条件下,求解把物质从源点传输到汇点的最大速率。本章主要介绍流网络和流的基本概念和性质,并提供流网络的数据结构描述和实现,以及一种解决最大流的经典方法及其算法实现,即Ford-Fulkerson方法。
1 流网络
网络流G=(v, E)是一个有向图,其中每条边(u, v)均有一个非负的容量值,记为c(u, v) ≧ 0。如果(u, v) ∉ E则可以规定c(u, v) = 0。网络流中有两个特殊的顶点,即源点s和汇点t。
与网络流相关的一个概念是流。设G是一个流网络,其容量为c。设s为网络的源点,t为汇点,那么G的流是一个函数f:V×V →R,满足一下性质:
l 容量限制:对所有顶点对u,v∈V,满足f(u, v) ≦ c(u, v);
l 反对称性:对所有顶点对u,v∈V,满足f(u, v) = - f(v, u);
l 流守恒性:对所有顶点对u∈V-{s, t},满足Σv∈Vf(u,v)=0。
f(u, v)称为从顶点u到顶点v的流,流的值定义为:
|f| =Σv∈Vf(s,v),
即从源点s出发的总的流。
在最大流问题中,我们需要求解源点s到汇点t之间的最大流f(s, t),同时我们还希望了解达到该值的流。对于一个指定的源点s和指定汇点t的网,我们称之为st-网。
如图所示为一个流网络,其中顶点之间的边的粗细对应着边的容量大小。
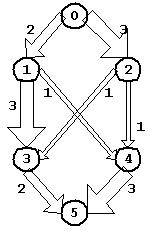
图 有向图表示网络流
下面以图为例,在流的三个性质条件下尝试性地寻找图中的最大流,如图(a~c)。
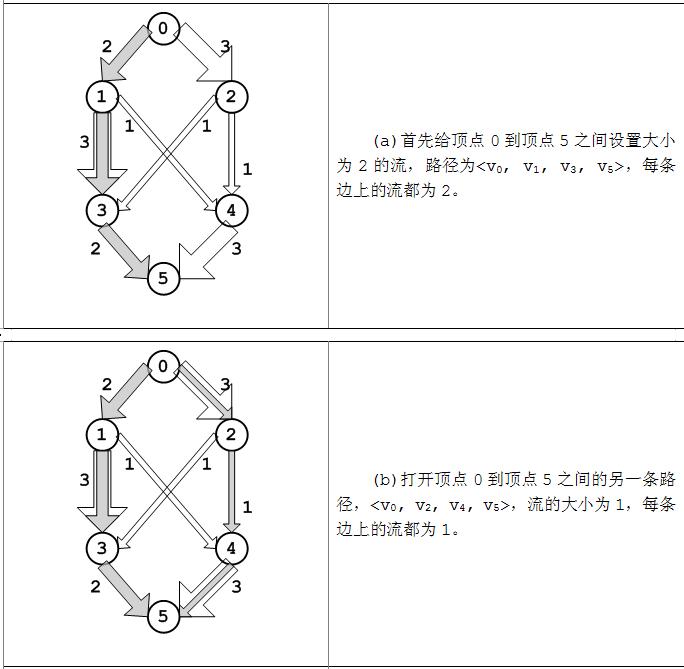
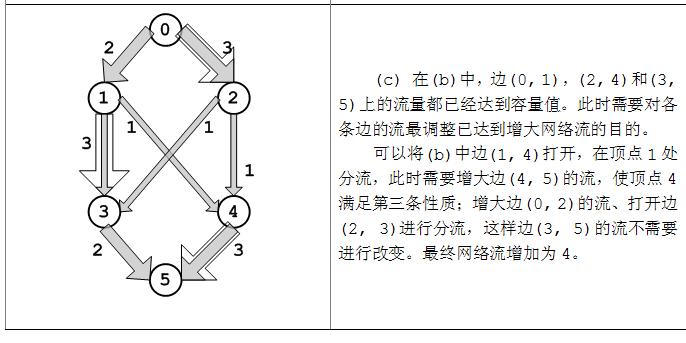
从上图(a~c)中可以发现,流网络从源点s流出的量依次为2,3,5,而流入汇点t的流量也2,3,5。事实上,任何流从s流出量总应该等于到汇点t的流入量,下面对这一命题做简单证明。

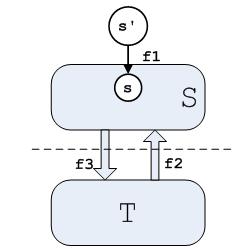
构造:如图(a),对原流网络做扩展,增加顶点s’和一条边(s’, s),边的流和容量都与从s流出的流的值相等;增加顶点t’和一条边(t, t’),边的流和容量都与到t的流的值相等。
我们要证明s’的流出量等于t’的流入量,只要证明对任意顶点集合,流出量等于流入量即可。采用归纳证明。
证明:对于单个顶点构成的顶点集合,其流出量必然等于流出量;假设,对于一给定的顶点集合A此属性成立,则需要验证增加一个顶点v后得到的新的集合A’=A∪{v}也满足此属性。
如图,对集合A,从v流入的流记为f3,其它的流入量合计为f1;流出到v的流记为f4,其它的流出流量合计为f6。注意,这里的流都指的是流的值,都是非负的。
A的流入量为fin(A) = f1 + f3,流出量为fout(A) = f2 + f4;根据假设可以得出关系:
f1 + f3 = f2 + f4;
对顶点v,根据流的第二条性质,得出关系:
f6 + f3 = f5 + f4。
根据上面两个等式,可以得到关系:
f1 – f6 = f2 – f5,
即:
f1 + f5 = f2 + f6。
A’的流入量fin(A’) = f1 + f5,流出量fout(A’) = f2 + f6,所以集合A’满足属性。
将这个属性应用于扩展前的原始流网络中的所有顶点,可以得出边(s’, s)上的流等于边(t’, t)上的流,也就是从s流出量等于到汇点t的流入量。
2 Ford-Fulkerson方法
本节开始讨论解决最大流问题的Ford-Fulkerson方法,该方法也称作“扩充路径方法”,该方法是大量算法的基础,有多种实现方法。在以后章节中我们将介绍并分析一种特定的算法。
Ford-Fulkerson算法是一种迭代算法,首先对图中所有顶点对的流大小清零,此时的网络流大小也为0。在每次迭代中,通过寻找一条“增广路径”(augument path)来增加流的值。增广路径可以看作是源点s到汇点t的一条路径,并且沿着这条路径可以增加更多的流。迭代直至无法再找到增广路径位置,此时必然从源点到汇点的所有路径中都至少有一条边的满边(即边的流的大小等于边的容量大小)。
这里提及一个新的概念,即“增广路径”。下面我们将进一步引入“残留网络”(residual network)来讨论增广路径的寻找算法,并引入“最大流最小割”(Max-Flow Min Cut)定理来证明Ford-Fulkerson算法的正确性。
2.1 残留网
给定一个流网络G和一个流,流的残留网Gf拥有与原网相同的顶点。原流网络中每条边将对应残留网中一条或者两条边,对于原流网络中的任意边(u, v),流量为f(u, v),容量为c(u, v):
l 如果f(u, v) > 0,则在残留网中包含一条容量为f(u, v)的边(v, u);
l 如果f(u, v) < c(u, v),则在残留网中包含一条容量为c(u, v) - f(u, v)的边(u, v)。
残留网允许我们使用任何广义图搜索算法来找一条增广路径,因为残留网中从源点s到汇点t的路径都直接对应着一条增广路径。以图为例,具体分析增广路径及其相应残留网,如图(a~d)。
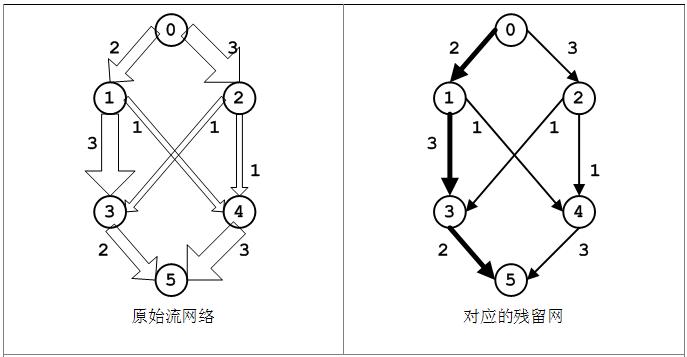
(a)原始图流网络,每条边上的流都为0。因为f(u, v) = 0 < c(u, v),则在残留网中包含容量为c(u, v)的边(u, v),所以此时残留图中顶点与原始流网络相同,边也与原始流网络相同,并且边的容量与原始流网络相同。
在残留网中可以找到一条增广路径<v0, v1, v3, v5>,每条边的流为2,此原始流网络和残留网中相应的边会有所变化,如下图。
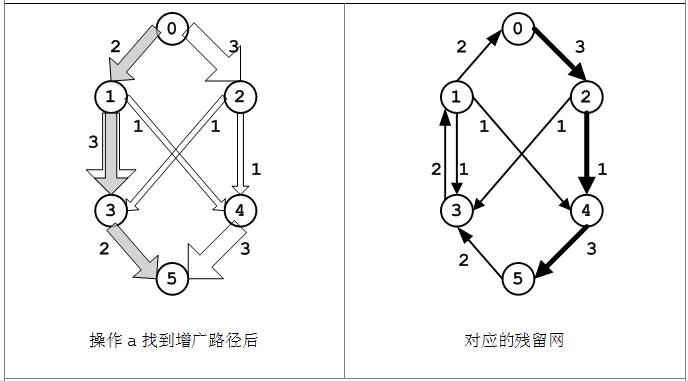
(b)在操作(a)之后,路径<v0, v1, v3, v5>上有了大小为2的流,此时需要对残留图中相应的边做调整:
f(0, 1) > 0,在残留图中有容量为2的边(1, 0);
c(1, 3) > f(1, 3) > 0,在残留图中有容量为1的边(1, 3)和容量为2的边(3, 1);
f(3, 5) > 0,在残留图中有容量为2的边(5, 3).
在残留网中可以找到一条增广路径<v0, v2, v4, v5>,每条边的流为1,此原始流网络和残留网会有所变化,如下图。
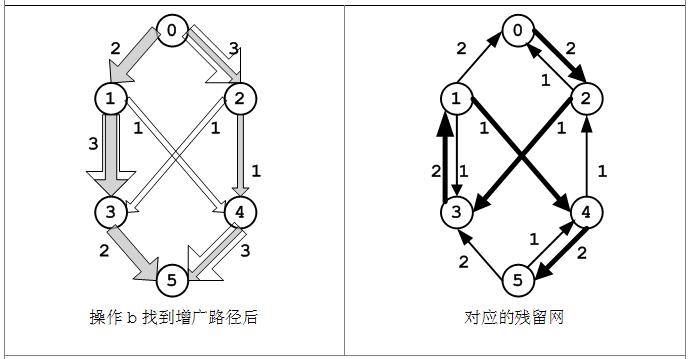
(c)在操作(b)之后,路径<v0, v2, v4, v5>上有了大小为1的流,此时需要对残留图中相应的边做调整:
c(0, 2) > f(0, 2) > 0,在残留图中有容量为2的边(0, 2)和容量为1的边(2, 0);
f(2, 4) > 0,在残留图中有容量为1的边(4, 2);
c(4, 5) > f(4, 5) > 0,在残留图中有容量为2的边(4, 5)和容量为1的边(5, 4).
进一步在残留网中可以找到一条增广路径<v0, v2, v3, v1, v4, v5>,每条边的流为1,此原始流网络和残留网会有所变化,如下图。

(d)在操作(c)之后,路径<v0, v2, v3, v1, v4, v5>上有了大小为1的流,此时需要对残留图中相应的边做调整:
c(0, 2) > f(0, 2) > 0,在残留图中有容量为1的边(0, 2)和容量为2的边(2, 0);
f(2, 3) > 0,在残留图中有容量为1的边(3, 2);
c(3, 1) > f(3, 1) > 0,在残留图中有容量为1的边(3, 1)和容量为2的边(1, 3);
f(1, 4) > 0,在残留图中有容量为1的边(4, 1);
c(4, 5) > f(4, 5) > 0,在残留图中有容量为1的边(4, 5)和容量为2的边(5, 4);
此时残留图中无法再找到顶点0到顶点5的路径,则迭代结束,我们认为图d中即为寻找到的最大流。
2.2 最大流最小割
我们刚刚讨论了基于残留网的增广路径的寻找方法,这里我们将证明Ford-Fulkerson算法迭代停止时得到的流是最大流,即一个流是最大流,当且仅当残留网中不包含增广路径。该命题的证明需要借助于流网络中的一个重要定理,即最大流最小割定理。
流网络G=(V, E)的割(S, T)将V分为S和T=V-S两个部分,使得源点s∈S,汇点t∈T。如果f是一个流,则穿过割(S, T)的流用f(S, T) = Σu∈SΣv∈T f(u, v)表示,割(S, T)的容量用C(S, T) = Σu∈SΣv∈T c(u, v)。如图,流网络的一个割为({s, v1, v2},{v3, v4, t})
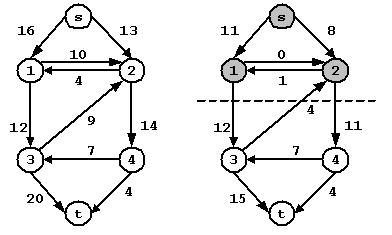
图 (a)流网络每条边上是容量大小 (b)流网络的一个割,边上是流的大小
通过该割的流量为:
f(S, T) = Σu∈{s, v1, v2}Σv∈{v3, v4, t} f(u, v)
= f(v1, v3) + f(v2, v3) + f(v2, v4)
= 12 + (-4) + 11 = 19
容量为:
C(S, T) = Σu∈{s, v1, v2}Σv∈{v3, v4, t} c(u, v)
= c(v1, v3) + c(v2, v4)
= 12 + 14 = 26
其中割的流可能是正数也可能是负数,而容量一定是非负的。在流网络中,每个割的流都是相同的,其值等于流网络的流的值;并且每个割的流都不大于割的容量。
如图,s’为扩展的顶点,其中边(s’, s)的流和容量都等于顶点s的流出量,记为f1。虚线将流网络分为两个集合S和T,形成割(S, T)。从S流出的流量为f2,流入S的流量为f3。在第一节中我们证明了流网络中的顶点集合的流入量等于流出量,所以f1 + f2 = f3。
即f1 = f3 – f2,其中f1等于流网络的流的值,f3-f2为割(S, T)的流量,所以,割的流等于流网络的流的值。
在上图中,计算割(S, T)的流量时f3的提供正的流量值,而f2提供的是负的流量值,并且在计算割的容量时只有提供流量f3的边的容量参与相加,根据流的第一条性质,f3的值不会大于割的容量,所以:
f(S, T) = f3 – f2 ≦ f3 ≦ C(S, T)。
由于流网络中所有割的流都相等并且等于网络的流,所有网络的任何流的值都不大于任何一个割的容量。
根据上面对流网络的中割的概念的介绍,下面引入最大流最小割定理,并利用该定理说明Ford-Fulkerson算法的正确性。
最大流最小割定理:一个网中所有流中的最大值等于所有割中的最小容量。并且可以证明一下三个条件等价:
l f是流网络G的一个最大流;
l 残留网Gf不包含增广路径;
l G的某个割(S, T),满足f(S, T) = c(S, T).
证明:
1.(反证法)假设f是G的最大流,但是Gf中包含增广路径p。显然此时沿着增广路径可以继续增大网络的流,则f不是G的最大流,与条件矛盾;
2.假设Gf中不包含增广路径,即Gf中不包含从s到t的路径。定义:
S = {v∈V:Gf中包含s到v的路径},
令T = V – S,由于Gf中不存在从s到t的路径,则t∉S,所以得到G的一个割(S, T)。对每对顶点u∈S,v∈T,必须满足f(u, v) = c(u, v),否则边(u, v)就会存在于Gf的边集合中,那么v就应当属于S(而事实上是v∈T)。所以,f(S, T) = c(S, T);
3.我们已经证明,网络的任何流的值都不大于任何一个割的容量,如果G的某个割(S, T),满足f(S, T) = c(S, T),则说明割(S, T)的流达到了网络流的上确界,它必然是最大流。
Ford-Fulkerson算法的迭代终止条件是残留网中不包含增广路径,根据上面的等价条件,此时得到的流就是网络的最大流。
3 Ford-Fulkerson方法的实现
在前一节,我们讨论了Ford-Fulkerson方法中所应用到的几个概念以及保证该方法正确性的重要属性。本节将讨论Ford-Fulkerson方法的具体实现,包括残留网的更新和增广路径的获取。
增广路径事实上是残留网中从源点s到汇点t的路径,可以利用图算法中的任意一种被算法来获取这条路径,例如BFS,DFS等。其中基于BFS的算法通常称为Edmonds-Karp算法,该算法是“最短”扩充路径,这里的“最短”由路径上的边的数量来度量,而不是流量或者容量。
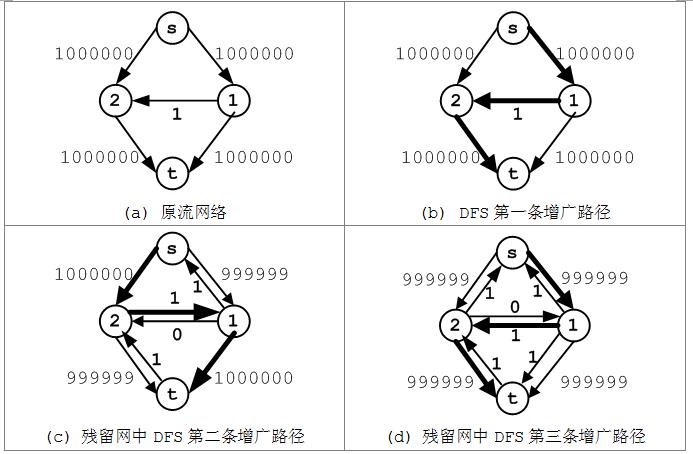
这里所选的路径寻找方法会直接影响算法的运行时间,例如,对图采用DFS的方法搜索残留网中的增广路径。图(b)中是第一次搜索得到的增广路径为<s, v1, v2, t>,路径的流大小为1;图(c)和(d)中搜索得到的增广路径的流大小也是1。可以发现,在这个例子中,采用DFS算法将需要2000000次搜索才能得到最大流。
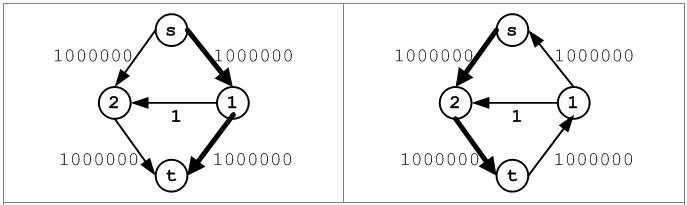
如果换一种方法对残留网中的进行遍历将会很快求得流网络的最大流。如图,第一次在顶点1搜索下一条边时,不是选择边(1, 2)而是选择容量更大的边(1, t);第二次在顶点2处搜索下一条边时,选择边(2, t)。这样只要两次遍历即可求解最大流。可见,在残留网中搜索增广路径的算法直接影响Ford-Fulkerson方法实现的效率。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号