牛客寒假算法基础集训营4 E Applese 涂颜色
链接:https://ac.nowcoder.com/acm/contest/330/E
思路:很简单,2^n,但是要注意n可以取到10的10万次方,此时要用到指数循环节降幂或者十进制快速幂(或者python)
题解:
1 #include <iostream> 2 #include <string> 3 #define ll long long 4 const ll mod = 1e9+7; 5 using namespace std; 6 ll quickPow(ll a,ll b) 7 { 8 ll ans = 1; 9 a %= mod; 10 while(b) 11 { 12 if(b&1) ans = (ans * a) % mod; 13 a = a * a % mod; 14 b >>= 1; 15 } 16 return ans; 17 } 18 ll euler(ll n) 19 { 20 ll res = n; 21 for(int i = 2; i*i < n; i++) 22 { 23 if(n % i == 0) 24 res = res / i * (i-1); 25 while(n%i==0) 26 n /= i; 27 } 28 if(n > 1) 29 res = res / n * (n-1); 30 return res; 31 } 32 int main() 33 { 34 string s1,s2; 35 while(cin>>s1>>s2) 36 { 37 ll length = s1.size(),n = 0,p; 38 //p = mod - 1; 39 p = euler(mod); 40 for(int i = 0; i < length; i++) 41 { 42 n =(n * 10 + (s1[i] - '0')) % p; 43 } 44 cout<<quickPow(2,n)<<endl; 45 } 46 return 0; 47 }
(抄的大佬的代码)
备注:大佬写的是指数循环节,用到欧拉降幂公式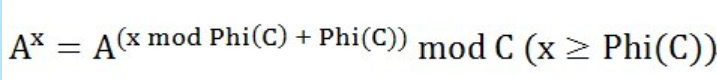
接下来放出python代码:
1 print(pow(2,int(input().split()[0]),10**9+7))
吐槽:我被震撼了,python太强大了。
总结——欧拉降幂公式
————————————————
心里有光,哪儿都美
心里有光,哪儿都美


