atcoder 做题记录
AGC043
B 123 Triangle
题意
给定长为 \(n\) 的序列 \(a\)。有递推关系 \(f_{k,x}=|f_{k-1,x}-f_{k-1,x+1}|(k>1,x\le n-k+1),f_{1,x}=a_x\)。求 \(f_{n,1}\)。
数据范围:\(n\le 10^6,1\le a_i\le 3\)
view solution
solution
先把 \(n=1\) 判掉,然后 \(a_i\in[0,2]\)。注意到 \(1\) 的特殊性:如果原序列存在 \(1\),那么最后答案一定是 \(0,1\) 中的一个。
对于 \(f_i\),如果存在一个 \(1\) 其左边/右边不是 \(1\),那么在 \(f_{i+1}\) 中一定存在至少一个 \(1\)。否则所有数都是 \(1\),\(f_{i+1}\) 中都是 \(0\)。
所以如果有 \(1\) 的话,只需要判断答案的奇偶性。注意到 \(|a-b|\bmod 2=a+b \bmod 2\),\(a_i\) 对 \(f_{n,0}\) 的贡献是 \(\binom{n-1}{i-1}\)。所以答案是
使用 Lucas 定理即可。
对于没有 \(1\) 的情况,把 \(2\) 视为 \(1\) 再跑即可。
view code
#include <bits/stdc++.h>
using namespace std;
const int N=1e6+5;
inline int binom(int n,int m){return (n&m)==m?1:0;}
int n,a[N];
char s[N];
int main(){
scanf("%d",&n);
scanf("%s",s+1);
for(int i=1;i<=n;++i)a[i]=s[i]-'0';
if(n==1){
printf("%d\n",a[1]);
return 0;
}
for(int i=1;i<n;++i)a[i]=abs(a[i]-a[i+1]);
--n;
bool flag=0;
for(int i=1;i<=n;++i){
if(a[i]==1)flag=1;
}
int key=flag?1:2;
int sum=0;
for(int i=1;i<=n;++i)
if(a[i]==key)sum^=binom(n-1,i-1);
printf("%d\n",sum?key:0);
return 0;
}
C Giant Graph
题意
给定三个简单无向图 \(G_1,G_2,G_3\),点数均为 \(n\)。
另根据这三张图构造一个有 \(n^3\) 个点的图 \(G\),图 \(G\) 上
- \(\forall (u,v)\in G_1,a,b\in[1,n]\),连边 \((u,a,b),(v,a,b)\)。
- \(\forall (u,v)\in G_2,a,b\in[1,n]\),连边 \((a,u,b),(a,b,v)\)。
- \(\forall (u,v)\in G_3,a,b\in[1,n]\),连边 \((a,b,u),(a,b,v)\)。
对于 \(G\) 中的任意一个点 \((x,y,z)\),定义其点权为 \(10^{18(x+y+z)}\)。
求 \(G\) 的最大权独立集的大小模 \(998244353\) 的值。
数据范围:\(n,m\le 10^5\)
view solution
solution
把原问题转博弈题。
首先因为一个点的权值很大,所以我们肯定优先选 \(x+y+z\) 大的,这样与 \((x,y,z)\) 有边相连的点肯定不能选。
我们把要选的点视为必败态,这样所有能一步走到必败态的点就是必胜态。答案是所有必胜态的点的权值之和。
把每张图边定向,从小的连向大的,这样变成一个博弈的 DAG,并求出所有点的 SG 函数。如果 \((x,y,z)\) 满足 \(sg_1(x)\oplus sg_2(y)\oplus sg_3(z)=0\),那么点 \((x,y,z)\) 是必败态,即我们需要选的点。注意到 \(sg\) 值是 \(O(\sqrt{n})\) 级别的,预处理每张图中,\(sg(a)=i\) 的所有 \(a\) 的 \(10^{18a}\) 之和,然后枚举 \(sg_1(x)\) 和 \(sg_2(y)\) 即可。复杂度 \(O(n+m)\)。
view code
#include <bits/stdc++.h>
using namespace std;
inline int read(){
int s=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9')s=(s<<3)+(s<<1)+ch-'0',ch=getchar();
return s*f;
}
const int N=1e5+5,mod=998244353;
inline int quick_pow(int a,int b){
int ret=1;
for(;b;b>>=1,a=1ll*a*a%mod)if(b&1)ret=1ll*ret*a%mod;
return ret;
}
const int pw=quick_pow(10,18);
int n;
struct Graph{
vector<int> e[N];
int cnt[N],sg[N],m,mx;
bool vis[N];
void dfs(int u){
if(sg[u]!=-1)return;
for(int v:e[u])
dfs(v);
for(int v:e[u])
vis[sg[v]]=1;
for(int i=0;;++i)if(!vis[i]){
sg[u]=i;
break;
}
for(int v:e[u])
vis[sg[v]]=0;
}
void work(){
m=read();
for(int i=1,u,v;i<=m;++i){
u=read();v=read();
if(u>v)swap(u,v);
e[u].push_back(v);
}
memset(sg+1,-1,n<<2);
for(int i=1;i<=n;++i){
dfs(i);cnt[sg[i]]=(cnt[sg[i]]+quick_pow(pw,i))%mod;
mx=max(mx,sg[i]);
}
}
}G1,G2,G3;
int main(){
n=read();
G1.work();
G2.work();
G3.work();
int ans=0;
for(int i=0;i<=G1.mx;++i)if(G1.cnt[i])
for(int j=0;j<=G2.mx;++j)if(G2.cnt[j])
if(G3.cnt[i^j])ans=(ans+1ll*G1.cnt[i]*G2.cnt[j]%mod*G3.cnt[i^j])%mod;
printf("%d\n",ans);
return 0;
}
D Merge Triplets
题意
有 \(n\) 个大小为 \(3\) 的序列,总共 \(3n\) 个元素,这 \(3n\) 个元素构成一个 \(1\sim 3n\) 的排列。
另有一个排列 \(P\),每次选出所有非空序列中的第一个元素中最小的一个,把这个元素放到 \(P\) 的末尾,并把它从其所在序列中删除。一直操作直到所有序列为空,即 \(P\) 变成一个 \(1\sim 3n\) 的排列。
对于所有生成 \(n\) 个序列的方式,求能生成多少个不同的排列 \(P\),答案取模。
数据范围:\(n\le 2000\)。
view solution
### solution对于一个大小为 \(3\) 的序列,它在 \(P\) 中的位置一定是下面三种情况之一:
- 一个长为为 \(3\) 的连续段
- 两个连续段,长度为 \(1+2/2+1\)
- 三个连续段,长度为 \(1,1,1\)
也就是,只要一个排列 \(P\) 满足以下限制,它一定能被构造出来:
能被前缀最大值分为若干段,每段的长度 \(\le 3\),且 \(2\) 的数量 \(\le 1\) 的数量。
DP,\(f_{i,j}\) 表示考虑完前 \(i\) 个数,\(1\) 的数量 \(-2\) 的数量 \(=j\) 的方案数。
复杂度 \(O(n^2)\)。
view code
#include <bits/stdc++.h>
using namespace std;
const int N=2005;
int C[N*3][3],mod;
inline int add(int a,int b){return (a+b>=mod)?a+b-mod:a+b;}
inline void init(int n){
C[0][0]=1;
for(int i=1;i<=n;++i){
C[i][0]=1;
for(int j=1;j<3;++j)C[i][j]=add(C[i-1][j-1],C[i-1][j]);
}
}
struct Val{
int f[6*N];
inline int& operator[](int x){return f[x+3*N];}
};
int n;
Val f[N*3];
int main(){
cin>>n>>mod;
init(n*3);
f[0][0]=1;
for(int i=1;i<=3*n;++i){
for(int j=1;j<=3&&j<=i;++j){
int v=C[i-1][j-1];
if(j==3)v=2ll*v%mod;
for(int k=-i+1;k<i;++k){
if(j==1)f[i][k+1]=(f[i][k+1]+1ll*v*f[i-j][k])%mod;
else if(j==2)f[i][k-1]=(f[i][k-1]+1ll*v*f[i-j][k])%mod;
else f[i][k]=(f[i][k]+1ll*v*f[i-j][k])%mod;
}
}
}
int ans=0;
for(int i=0;i<=3*n;++i)ans=add(ans,f[3*n][i]);
printf("%d\n",ans);
return 0;
}
E Topology
题意
平面上有 \(n\) 个点,分别位于 \((i+\frac{1}{2},\frac{1}{2})(i\in[0,n-1])\),以及一个封闭曲线 \(C\)。给定 \(2^n\) 个状态,每个状态 \(f_S\) 表示在考虑 \(S\) 集合内的所有点时,曲线 \(C\) 能否在不接触 \(S\) 集合内的点,移动到所有点的纵坐标都 \(<0\) 的位置。
请你根据 \(f\) 构造一个满足条件的 \(C\),或者判定无解。
数据范围:\(n\le 8\)
view solution
首先容易发现,\(f\) 具有传递性,即如果 \(f_{S}=1\),那么对于 \(T\subseteq S,f_{T}=1\);如果 \(f_{S}=0\),那么对于 \(S\subseteq T,f_{T}=0\)。如果违反了传递性显然无解。
我们现在找到所有的 \(S\),满足所有 \(S\) 的子集都能解出来,\(S\) 及 \(S\) 的所有超集都不能被解出来。如果我们的构造满足:对于 \(S\) 无法解出,而删掉任何一个点都能解出,那么我们把所有 \(S\) 的构造连到同一个点上把它们拼起来,就满足了题面的所有限制。
构造之前,先考虑 spj 怎么写:从封闭曲线的一个点出发走一圈,如果经过点 \(i\) 的上方,往序列里写下一个 \(u_i\);如果经过点 \(i\) 的下方,写下一个 \(t_i\)。如果出现了连续的 \(u_i,u_i\) 或者 \(t_i,t_i\),那么这两步可以删掉,不会影响 \(i\) 是否被 \(C\) 包住,也就不会影响 \(C\) 是否能解出。如果一直把整个序列都删完了,那么不存在任何一个点被包住,即 \(C\) 可以解出,否则 \(C\) 无法解出。
会了判定之后递归构造方案(方案要满足:对于 \(S\) 无法解出,而删掉任何一个点都能解出):
- 如果当前集合内只有 \(1\) 个点,把这个点包一圈即可
- 先把最靠左的 \(i\) 去掉,设 \(T\) 表示 \(S'=S\setminus \{i\}\) 的方案,那么我们构造 \(u_iTu_it_iT't_i\),\(T'\) 表示把 \(T\) 中的方案倒序之后的方案。容易发现,如果任何一个点被删掉(删掉它的所有 \(u_i,t_i\)),那么整个序列就能被删完;否则整个序列不能被删掉任何一个元素。
view code
#include <bits/stdc++.h>
using namespace std;
const int N=10;
#define pr pair<int,int>
#define mp make_pair
#define fi first
#define se second
#define pb push_back
#define ins(x,y) ret.pb(mp(x,y))
inline vector<pr> solve(int s,int pre){
int x=__builtin_ctz(s);
vector<pr> ret;
for(int i=pre+1;i<=x;++i)
ins(i,0);
if(__builtin_popcount(s)==1){
ins(x+1,0);ins(x+1,1);
ins(x,1);ins(x,0);
for(int i=x;i>pre;--i)
ins(i-1,0);
return ret;
}
ins(x+1,0);
vector<pr> T=solve(s^(1<<x),x+1);
for(pr p:T)ret.pb(p);
ins(x,0);
ins(x,1);
ins(x+1,1);
ins(x+1,0);
T.pop_back();
reverse(T.begin(),T.end());
for(pr p:T)ret.pb(p);
ins(x+1,0);
ins(x+1,1);
ins(x,1);
ins(x,0);
for(int i=x-1;i>=pre;--i)ins(i,0);
return ret;
}
int n;
char s[1<<N];
int a[N],f[1<<N];
vector<pr> ans;
int main(){
scanf("%d",&n);
scanf("%s",s);
int tot=(1<<n);
for(int i=0;i<tot;++i){
f[i]=s[i]-'0';
for(int j=0;j<n;++j)
if(i&(1<<j)){
if(f[i]==1&&f[i^(1<<j)]==0){
puts("Impossible");
return 0;
}
}
}
ans.pb(mp(0,0));
for(int i=1;i<tot;++i){
if(!f[i]){
bool flag=1;
for(int j=0;j<n;++j)if(i&(1<<j)){
if(!f[i^(1<<j)])flag=0;
}
if(flag){
vector<pr> cur=solve(i,0);
for(pr p:cur)ans.pb(p);
}
}
}
puts("Possible");
printf("%d\n",(int)ans.size()-1);
for(pr p:ans)printf("%d %d\n",p.fi,p.se);
return 0;
}
F Jewelry Box
题意
有 \(N\) 个珠宝商店。
每个商店卖 \(K_i\) 种珠宝,第 \(i\) 个商店的第 \(j(1\le j\le K_i)\) 种珠宝拥有三个独立的属性 \((S,P,C)\) 依次表示重量,价格,数量。
现在有 \(Q\) 组询问,每次给定一个 \(A_i\),询问能否够构造 \(A_i\) 个“珠宝盒”,如果可以则输出最小的花费(即购买的珠宝的价格之和)否则输出 \(-1\)
一个“珠宝盒”是一个包含 \(N\) 个珠宝的盒子,且满足如下条件:
- 盒子内部的第 \(i\) 个珠宝从第 \(i\) 个珠宝商店处购买。
- 满足 \(M\) 条约束:
- 对于第 \(i\) 条约束:此盒子内第 \(V_i\) 珠宝的重量应当不超过第 \(U_i\) 个珠宝的重量 \(+ W_i\)
数据范围:
\(N,K_i\le 30,S_{i,j}\le 10^9,P_{i,j}\le 30,C_{i,j}\le 10^{12},M\le 50,Q\le 10^5,A_i\le 3\times 10^{13},W_i\le 10^9\)
view soluiton
参见 sxTQX 的博客 线性规划对偶问题
view code
#include <bits/stdc++.h>
using namespace std;
#define int long long
inline int read(){
int s=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9')s=(s<<3)+(s<<1)+ch-'0',ch=getchar();
return s*f;
}
namespace Flow{
const int M=1e5+5,N=1e5+5,inf=1e17;
struct Edge{int to,next,flow,cost;}e[M];
int dis[N],head[N],cur[N],tot,ecnt=1,h[N],p[N];
inline void adde(int u,int v,int flow,int cost){
e[++ecnt]=(Edge){v,head[u],flow,cost};head[u]=ecnt;
e[++ecnt]=(Edge){u,head[v],0,-cost};head[v]=ecnt;
}
bool inq[N];
bool SPFA(int s,int t){
memset(dis+1,0x3f,tot<<3);
dis[s]=0;
queue<int> q;
q.push(s);
while(!q.empty()){
int u=q.front();q.pop();
inq[u]=0;
cur[u]=head[u];
for(int i=head[u],v;i;i=e[i].next){
if(!e[i].flow)continue;
v=e[i].to;
if(dis[v]>dis[u]+e[i].cost){
dis[v]=dis[u]+e[i].cost;
if(!inq[v])q.push(v),inq[v]=1;
}
}
}
memcpy(p+1,dis+1,tot<<3);
return dis[t]<=inf;
}
bool dijkstra(int s,int t){
for(int i=1;i<=tot;++i)h[i]+=p[i];
priority_queue<pair<int,int> > q;
q.push(make_pair(0,s));
memset(dis+1,0x3f,tot<<3);
memset(inq+1,0,tot);
dis[s]=0;
while(!q.empty()){
int u=q.top().second;q.pop();
if(inq[u])continue;
inq[u]=1;
cur[u]=head[u];
for(int i=head[u],v;i;i=e[i].next){
if(!e[i].flow)continue;
v=e[i].to;
if(dis[v]>dis[u]+e[i].cost-h[v]+h[u]){
dis[v]=dis[u]+e[i].cost-h[v]+h[u];
q.push(make_pair(-dis[v],v));
}
}
}
memcpy(p+1,dis+1,tot<<3);
return dis[t]<=inf;
}
bool vis[N];
int dinic(int u,int t,int flow){
if(u==t)
return flow;
vis[u]=1;
int ret=0,f;
for(int&i=cur[u];i;i=e[i].next){
int v=e[i].to;
if(!e[i].flow||dis[v]!=dis[u]+e[i].cost-h[v]+h[u]||vis[v])continue;
f=dinic(v,t,min(flow,e[i].flow));
e[i].flow-=f;e[i^1].flow+=f;
ret+=f;flow-=f;
}
vis[u]=0;
if(f)dis[u]=inf;
return ret;
}
}
const int N=55,inf=1e17;
int s[N][N],p[N][N],c[N][N],s1[N],p1[N],c1[N],k[N],n,id[N][N],tot;
int cnt,flow[N*N],cost[N*N],F[N*N],m,per[N];
inline bool cmp(int x,int y){
return s1[x]<s1[y];
}
signed main(){
n=read();
int S=++tot,T=++tot;
for(int i=1;i<=n;++i){
k[i]=read();
for(int j=1;j<=k[i];++j){
s1[j]=read();
p1[j]=read();
c1[j]=read();
if(j>1)id[i][j]=++tot;
else id[i][j]=S;
per[j]=j;
}
sort(per+1,per+1+k[i],cmp);
for(int j=1;j<=k[i];++j){
s[i][j]=s1[per[j]];
p[i][j]=p1[per[j]];
c[i][j]=c1[per[j]];
}
id[i][k[i]+1]=++tot;
for(int j=2;j<=k[i]+1;++j){
Flow::adde(id[i][j-1],id[i][j],p[i][j-1],0);
Flow::adde(id[i][j-1],id[i][j],inf,c[i][j-1]);
Flow::adde(id[i][j],id[i][j-1],inf,0);
}
Flow::adde(id[i][k[i]+1],T,inf,0);
}
Flow::tot=tot;
m=read();
while(m--){
int u,v,w;
u=read();v=read();w=read();
int flag=1;
for(int i=1;i<=k[v];++i){
while(flag<=k[u]&&s[u][flag]+w<s[v][i])++flag;
Flow::adde(id[v][i],id[u][flag],inf,0);
}
}
int mf=0,mc=0;
for(Flow::SPFA(S,T);Flow::dijkstra(S,T);){
int f=Flow::dinic(S,T,inf);
flow[++cnt]=mf;
cost[cnt]=mc;
int d=Flow::dis[T]+Flow::h[T]-Flow::h[S];
F[cnt]=d;
if((__int128)f*d>=inf)break;
mf+=f;
mc+=f*d;
}
int q=read();
while(q--){
int a=read();
int i=lower_bound(F+1,F+cnt+1,a)-F;
if(i>cnt)
puts("-1");
else printf("%lld\n",flow[i]*a-cost[i]);
}
return 0;
}
AGC041
B Voting Judges
题意
有 \(n\) 个数 \(a_1,a_2,\dots,a_n\) ,需要进行 \(m\) 次操作,每次可以选择恰好 \(v\) 个数使其加上\(1\)。
操作完成之后将 \(a_1,a_2,\dots,a_n\) 按照不升的顺序排序(相同可以任意摆放),试问如果任意操作,原序列有多少个数有可能最后被排到前 \(p\) 位。
数据范围:\(n\le 10^5,\ v,p<n,\ a_i,m\le10^9\)。
view solution
solution
首先二分答案 \(mid\),然后先把所有 \(a_i>mid+m\) 的所有数都进行 \(m\) 次操作,所有 \(a_i+m\le mid\) 的都进行 \(m\) 次操作。假设现在还允许 \(k\) 个数最后 \(>mid\),把这现在最小的 \(k\) 个也进行 \(m\) 次操作。
然后就要求剩下的所有数能把剩下的所有操作做完且不存在一个 \(>mid\) 的数即可。
复杂度 \(O(n\log n)\)
view code
#include <bits/stdc++.h>
using namespace std;
inline int read(){
int s=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9')s=(s<<3)+(s<<1)+ch-'0',ch=getchar();
return s*f;
}
const int N=1e5+5;
int a[N],n,m,v,_v,p,b[N];
#define ll long long
inline bool check(int x){
v=_v;
memset(b+1,0,n<<2);
int cnt=1;
b[x]=1;
for(int i=1;i<=n;++i)if(a[i]>a[x]+m)b[i]=1,++cnt;
if(cnt>p)return 0;
for(int i=n;i>=1;--i)if(cnt<p&&!b[i])++cnt,b[i]=1;
v-=p;
if(v<=0)return 1;
ll sum=0;
for(int i=1;i<=n;++i)if(!b[i])sum+=min(m,a[x]+m-a[i]);
return sum>=1ll*v*m;
}
int main(){
n=read();m=read();_v=read();p=read();
for(int i=1;i<=n;++i)a[i]=read();
sort(a+1,a+1+n);
int l=1,r=n,ret,mid;
while(l<=r){
mid=(l+r)>>1;
if(check(mid)){
ret=mid;
r=mid-1;
}else l=mid+1;
}
printf("%d\n",n-ret+1);
return 0;
}
C Domino Quality
题意
你有一个 \(n\times n\) 的棋盘。
你需要在棋盘上放若干个 \(1 \times 2\) 或者 \(2 \times 1\) 的多米诺骨牌。
若放置完毕后,每一行和每一列的多米诺骨牌数量相同则合法。(注意,如果一个 \(1 \times 2\) 的多米诺骨牌放在了某一行上,只算它出现一次。列同理。)
请你给出一个合法的方案。若不存在则输出 -1。
数据范围:$2\le n\le 1000 $
view solution
### solution\(1,2\) 显然无解,特判 \(3\):
112
4 2
433
然后我们可以构造 \(4\times 4,5\times 5,7\times 7\) 的答案,满足每行每列的骨牌数量都是 \(3\):
- \(4\):
1134
2234
5677
5688
- \(5\):
123
123
44778
552 8
66299
- \(7\):
123
123
456
456
7788 9
1122 9
334455
如果 \(a\times a\) 和 \(b\times b\) 的方案中每行每列的骨牌数量都是 \(x\),那么我们把他们拼起来即可构成一个 \((a+b)\times (a+b)\) 的,每行每列的骨牌数量都是 \(x\) 的方案。
这样我们能通过 \(3\) 的方案构造 \(n=6\) 的,通过 \(4,5,7\) 的构造所有 \(n\ge 7\) 的。这样就做完了。
view code
#include<bits/stdc++.h>
using namespace std;
const int N=1010;
const int ans3[3][3]={{1,1,2},{4,0,2},{4,3,3}};
const int ans4[4][4]={{1,1,3,4},{2,2,3,4},{5,6,7,7},{5,6,8,8}};
const int ans5[5][5]={{0,0,1,2,3},{0,0,1,2,3},{4,4,7,7,8},{5,5,10,0,8},{6,6,10,9,9}};
const int ans7[7][7]={{0,0,0,0,1,2,3},{0,0,0,0,1,2,3},{0,0,0,0,4,5,6},{0,0,0,0,4,5,6},{7,7,8,8,0,0,9},{10,10,11,11,0,0,9},{12,12,13,13,14,14,0}};
int sz,n,pre[N],f[N],ans[N][N];
inline void insert(int x){
if(x==3){
for(int i=1;i<=x;++i)for(int j=1;j<=x;++j)
ans[sz+i][sz+j]=ans3[i-1][j-1];
}else if(x==4){
for(int i=1;i<=x;++i)for(int j=1;j<=x;++j)
ans[sz+i][sz+j]=ans4[i-1][j-1];
}else if(x==5){
for(int i=1;i<=x;++i)for(int j=1;j<=x;++j)
ans[sz+i][sz+j]=ans5[i-1][j-1];
}else if(x==7){
for(int i=1;i<=x;++i)for(int j=1;j<=x;++j)
ans[sz+i][sz+j]=ans7[i-1][j-1];
}
sz+=x;
}
void dfs(int x){
if(!x)return;
dfs(x-pre[x]);
insert(pre[x]);
}
int main(){
cin>>n;
if(n<=2){
puts("-1");
return 0;
}
if(n%3==0){
while(sz<n)insert(3);
}else{
for(int c:{4,5,7})f[c]=1,pre[c]=c;
for(int i=4;i<=n;++i)if(f[i]){
for(int c:{4,5,7})
if(!f[i+c])f[i+c]=1,pre[i+c]=c;
}
dfs(n);
}
for(int i=1;i<=n;++i){
for(int j=1;j<=n;++j){
if(ans[i][j])putchar(ans[i][j]+'a'-1);
else putchar('.');
}
puts("");
}
return 0;
}
D Problem Scores
题意
有 \(n\) 道还未赋分的题目,你需要给这 \(n\) 道题目赋分。
设第 \(i\) 道题目的分数为 \(A_i\)。给题目赋分的方案需要满足:
- 对于任意 \(i \in [2, n]\),\(A_{i-1} \leq A_{i}\)。
- 对于任意 \(i \in [1, n]\),\(1 \leq A_{i} \leq n\)。
- 对于任意一个大小为 \(k\)(\(1 \leq k < n\))的题目子集 \(S\) 和任意一个大小为 \(k+1\) 的题目子集 \(T\),需要满足:\(\sum_{x \in S}A_x < \sum_{x\in T}A_x\)。
你需要计算,有多少种给题目赋分的方案,使得能满足上述三个条件。请求出答案对 \(M\) 取模的结果。
数据范围:$ 2\le n\le5000 \(,\)M$ 是质数
view solution
solution
记 \(k=\lfloor\frac{n}{2}\rfloor\),我们只需要前 \(k+1\) 个数的和严格 \(>\) 后 \(k\) 个数的和。
我们把每个序列视为通过如下操作得到的序列:初始时每个元素都是 \(n\),每次选择一个前缀,对这个前缀都 \(-1\)。
我们 DP 就只需要维护前 \(k+1\) 个数和后 \(k\) 个数的差。序列上 \(n\) 个位置,每个位置都可以减任意次,每次对这个差的减小量是定值。做一个完全背包的计数即可。
复杂度 \(O(n^2)\)。
view code
#include <bits/stdc++.h>
using namespace std;
const int N=10005;
int len,n,mod,f[N],g[N],w[N],tot;
inline void Add(int &a,int b){a+=(a+b>=mod)?b-mod:b;}
int main(){
cin>>n>>mod;
if(n==1){
puts("1");
return 0;
}else if(n==2){
puts("3");
return 0;
}
int len=(n-1)>>1;
for(int i=1;i<=len+1;++i)w[++tot]=i;
if(!(n&1))w[++tot]=len+1;
for(int i=1;i<=len;++i)w[++tot]=i;
f[n]=1;
for(int i=1;i<=tot;++i)
for(int j=n;j>=0;--j)
Add(f[j],f[j+w[i]]);
int ans=0;
for(int i=1;i<=n;++i)Add(ans,f[i]);
printf("%d\n",ans);
return 0;
}
E Balancing Network
题意
有 \(n\) 根导线,\(m\) 个平衡器连接从左至右依次连接两个导线,如下图。
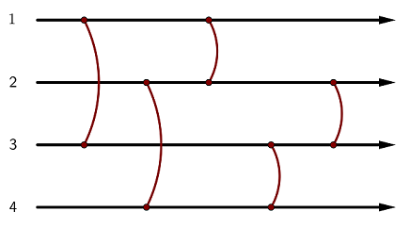
你需要给 \(m\) 个平衡器定向,电流从每根导线的最左侧出发,经过平衡器就会沿平衡器的方向流向另外一根导线。有两种类型的询问,第一种要求构造一个给平衡器定向的方案使得所有电流最后都在同一条导线上;第一种要求构造一个给平衡器定向的方案使得存在两个电流不在导线上。
可能无解。
数据范围:\(n,m\le 10^5\)
view solution
solution
- 第一种询问
我们维护 \(f_x\) 表示从当前位置出发,导线 \(x\) 的电流最终能到哪些位置。
从后往前枚举平衡器,\(f_x\gets f_x|f_y\),\(f_y\gets f_x|f_y\) 即可。最后全部与起来就能找到最终的终点是哪个,根据这个终点再从后往前构造即可。复杂度 \(O(\frac{nm}{\omega})\)。
- 第二种询问
显然 \(n=2\) 时无解。
从后往前枚举,维护当前时刻 \(cnt_i\) 表示所有导线从当前位置出发,以 \(i\) 结尾的不同开头有多少条。我们只要保证任意时刻都不存在 \(cnt_i>N\) 即可。同时维护 \(ed_x\) 表示从当前位置的 \(x\) 导线出发,最终能到达哪个终点。
对于一条边 \((x,y)\),如果 \(ed_x=ed_y\),显然随便指定一个方向即可。如果 \(cnt_{ed_x}=n-1\),那么把定向为 \(x\to y\),\(cnt_{ed_y}+1,cnt_{ed_x}-1\);如果 \(cnt_{ed_y}=n-1\),那么把定向为 \(y\to x\),对 \(cnt\) 的改变类似;其它情况随便定向。因为不存在两个 \(cnt\) 都是 \(n-1\) 的情况(\(\forall n>2,2(n-1)>n\)),所以一定有解。复杂度 \(O(m)\)。
view code
#include <bits/stdc++.h>
using namespace std;
inline int read(){
int s=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9')s=(s<<3)+(s<<1)+ch-'0',ch=getchar();
return s*f;
}
const int N=5e4+5,M=1e5+5;
bitset<N> f[N],tot;
int n,m,opt,x[M],y[M],g[N],ans[M];
inline void work1(){
for(int i=1;i<=n;++i)f[i].set(i),tot.set(i);
for(int i=m;i>=1;--i)
f[x[i]]=f[y[i]]=f[x[i]]|f[y[i]];
for(int i=1;i<=n;++i)tot&=f[i];
if(!tot.count())puts("-1");
else{
int p=tot._Find_first();
g[p]=1;
for(int i=m;i>=1;--i){
if((g[x[i]]||g[y[i]])&&g[x[i]]!=g[y[i]]){
if(!g[y[i]])ans[i]=1;
g[x[i]]=g[y[i]]=1;
}
}
for(int i=1;i<=m;++i){
if(ans[i]==1)putchar('^');
else putchar('v');
}
puts("");
}
}
int cnt[N],ed[N];
inline void work2(){
if(n==2){
puts("-1");
return ;
}
for(int i=1;i<=n;++i)cnt[i]=1,ed[i]=i;
for(int i=m;i>=1;--i){
if(cnt[ed[y[i]]]==n-1){
--cnt[ed[y[i]]];
ed[y[i]]=ed[x[i]];
++cnt[ed[x[i]]];
ans[i]=1;
}else{
--cnt[ed[x[i]]];
ed[x[i]]=ed[y[i]];
++cnt[ed[x[i]]];
}
}
for(int i=1;i<=m;++i){
if(ans[i]==1)putchar('^');
else putchar('v');
}
puts("");
}
int main(){
n=read();m=read();
opt=read();
for(int i=1;i<=m;++i)x[i]=read(),y[i]=read();
if(opt==1)work1();
else work2();
return 0;
}
F Histogram Rooks
题意
有一个 \(n\) 列的棋盘,第 \(i\) 列棋盘从下往上有 \(h_i\) 个格子。一个車会占据一个方格,如果一个方格所在的同一行或同一列中有一个車而且方格与車之间没有已被切除的格子,那么这个方格就被車所覆盖。特别的,若方格上就是車,那么该方格也被車覆盖。
求放車使得所有格子都被覆盖的方案数 \(\bmod 998244353\)。
数据范围:\(n,h_i\le 400\)
view solution
### solution考虑容斥,钦定有 \(k\) 个位置不会被任何一个車覆盖到。容斥系数为 \((-1)^k\),这时若有 \(x\) 个位置能放車,那么贡献是 \((-1)^k2^x\)。
我们枚举列的集合 \(S\),要求 \(S\) 中的每一列都至少有一个位置不能被車覆盖。
枚举所有行的连续段,假设其长度是 \(len\),这一个行连续段所包含的列与 \(S\) 的交集大小为 \(p\)。有如下两种贡献:
- 这一个连续段中的 \(p\) 个位置里不存在没有被覆盖的格子,那么除了这 \(p\) 列其他的都可以随便放車,容斥系数是 \(1\),方案数是 \(2^{len-p}\),总贡献是 \(2^{len-p}\)
- 这一个连续段中的 \(p\) 个位置里存在没有被覆盖的格子,那么这个连续段里不能放車,总贡献是 \(\sum_{i=1}^p\binom{p}{i}(-1)^i=-[p>0]\)
把所有连续段的贡献乘起来即可。但是此时我们没有保证 \(S\) 中的每一列都至少有一个位置不能被車覆盖。再枚举 \(T\subseteq S\) 表示 \(T\) 中的列的所有位置均被車覆盖。那么上面第一种贡献不变,第二种变成 \(\sum_{i=1}^{p-q}\binom{p-q}{i}(-1)^i=-[p-q>0]\)。
这样我们只关心 \(p\) 和 \([p>q]\)。
我们把原序列建出笛卡尔树,一个节点 \(u\) 的 \(p\) 是其所有儿子的 \(p\) 之和,其 \([p>q]\) 是其所有儿子的 \([p>q]\) 的与。这样 DP,维护 \(f_{u,p,[p>q]}\) 即可,转移是树形背包,复杂度 \(O(n^2)\)。
我们要建的也不完全是笛卡尔树,我们每次把当前区间内的最小值拿出来,这个最小值会把这个区间分成若干段,我们把这些段的关系建树,同时特殊处理一下最小值对应的位置即可。
view code
#include <bits/stdc++.h>
using namespace std;
inline int read(){
int s=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9')s=(s<<3)+(s<<1)+ch-'0',ch=getchar();
return s*f;
}
const int N=405,mod=998244353,inf=1e9;
inline int add(int a,int b){return a+b>=mod?a+b-mod:a+b;}
inline void Add(int &a,int b){a+=(a+b>=mod)?b-mod:b;}
inline int quick_pow(int a,int b){
int ret=1;
for(;b;b>>=1,a=1ll*a*a%mod)if(b&1)ret=1ll*ret*a%mod;
return ret;
}
int h[N];
int len[N],inde;
vector<int> e[N];
int build(int l,int r,int pre){
int mn=inf,u=++inde;
for(int i=l;i<=r;++i)mn=min(mn,h[i]);
len[u]=mn-pre;
int p=l;
for(int i=l;i<=r;++i){
if(h[i]!=mn)continue;
if(p<i)
e[u].push_back(build(p,i-1,mn));
e[u].push_back(0);
p=i+1;
}
if(p<=r)e[u].push_back(build(p,r,mn));
return u;
}
int f[N][N][2],sz[N],f1[N][2];
void dfs(int u){
if(!u)return;
f[u][0][1]=1;
sz[u]=0;
for(int v:e[u]){
dfs(v);
memset(f1,0,sizeof(f1));
for(int i=0;i<=sz[u];++i){
for(int j=0;j<=sz[v];++j){
for(int x:{0,1})for(int y:{0,1})
f1[i+j][x&y]=(f1[i+j][x&y]+1ll*f[u][i][x]*f[v][j][y])%mod;
}
}
sz[u]+=sz[v];
for(int i=0;i<=sz[u];++i)f[u][i][0]=f1[i][0],f[u][i][1]=f1[i][1];
}
for(int i=0;i<=sz[u];++i){
int base=quick_pow(2,sz[u]-i);
f[u][i][0]=1ll*f[u][i][0]*quick_pow(base-1,len[u])%mod;
f[u][i][1]=1ll*f[u][i][1]*quick_pow(base,len[u])%mod;
}
}
int n;
int main(){
f[0][0][1]=1;
f[0][1][0]=1;
f[0][1][1]=mod-1;
sz[0]=1;
n=read();
for(int i=1;i<=n;++i)h[i]=read();
int rt=build(1,n,0);
dfs(rt);
int ans=0;
for(int i=0;i<=sz[rt];++i)Add(ans,add(f[rt][i][0],f[rt][i][1]));
printf("%d\n",ans);
return 0;
}


