APIO2021暴毙记 and 题解
游记
Day -2
浓重湖南口音的《决策单调性和四边形不等式》
Day -1
在从镇海回成都的机场听了半节课
Day 0
《组合计数问题的常用技巧》,听着感觉还行
Day 1
主要是因为这篇题解咕的太久了考试时的内心想法快忘完了,只记得T1很毒,T2看着很可做但是不会,暴力跑路了,机房大佬都切了T3就我不会。然后T1打的暴力因为看错数据范围和细节写挂痛失一堆分(没准加上我就Ag了?)。
疯狂吐槽就此开始
- 没有大样例太难受了吧
- T3 居然是CF1119F原题
- 评测机刚开始的时候还是正常的,然后就越来越慢越来越慢,然后评测机就没了。一个小时之后它好了,然后啥都测不出来,连发两个公告
There is currently a long submission queue and we are currently working to make the evaluation of the submissions faster. Please be patient and rest assured that you submissions will be evaluated. Please do not resubmit your submission to reduce the large rate of the submissions.
We are currently experiencing a huge queue to evaluate submissions. You may keep submitting your solutions, and these submissions will be judged at some point after the contest. There will NOT be any time extension.
queueforces:评测long queue,题目codeforces
Day 2
\(43pts\) Cu
只记得计算几何的\(2^{2^d}\)的常数,和不知道在讲什么的半平面交。还有讲T2不知道假了多少遍的讲题人。
T1 六边形领域 hexagon
题意
有一个六边形网格,每个格子是一个六边形。给定一个封闭,简单,暴露的多边形,从起点开始BFS,将内部的六边形分层,定义\(f(x)=A+Bx\),求\(\sum_{i\in Polygon} f(dep_i)\mod 10^9+7\)
数据范围:边数\(\le 2\times 10^5\),边长之和\(\le 10^9\)
solution
多边形剖分
T2 雨林跳跃 jumps
题意
你有一排树,高度互不相同。每次只能从一棵树跳到左边/右边第一颗比它高的树上,多组询问,求从\([A,B]\)中任选一个出发,到达\([C,D]\)的任意一个的最小步数。无解输出\(-1\)
数据范围:\(n\le 2\times 10^5,q\le 10^5,1\le h_i\le n,A\le B<C\le D\)
solution
首先判断无解:\([B+1,C-1]\)中的最大值比\([C,D]\)中的大,其他时候一定有解,一直往右即可
现在考虑从哪个起点出发。显然我们的起点必须满足\([x,B]\)以内的数都\(\le h_x\)。
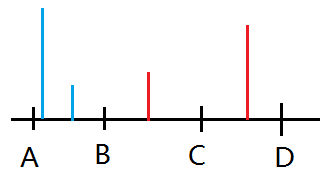
记\([B+1,C-1]\)中的最大值为\(a\),\([C,D]\)中的最大值为\(b\)。如果我们的高度到了\([a,b]\),那么我们就可以一步跳过去了。
我们从最右边往左倍增地跳,如果找到了一个高度在\([a,b]\)范围内的,直接返回\(1\)即可。否则我们为了尽快的让高度达到\([a,b]\)之间,我们选择小于\(b\)的最高的那个。
有一个显然的结论是:我们如果有一步右边比左边低,我们选择往右走最优的话,剩下的步所有我们都会往右走。因为再往左走的话显然不优。所以我们贪心的一直往左右两边较高的一处走。但是我们什么时候开始往右呢?因为要尽量使得高度增长快,直到不能选择更高的一边的时候(更高的一边高度\(> b\)),才会选择往右走。
倍增模拟这个过程即可
#include <bits/stdc++.h>
using namespace std;
const int N=200005,inf=1e9,LOG=20;
int n,stac[N],top,h[N],high[N][LOG],rght[N][LOG],lft[N][LOG];
inline int maxx(int a,int b){return h[a]>h[b]?a:b;}
int st[N][LOG],Log2[N];
inline int query(int l,int r){
if(l>r)return 0;
static int len;
len=Log2[r-l+1];
return max(st[l][len],st[r-(1<<len)+1][len]);
}
void init(int N,vector<int> H) {
n=N;
for(int i=1;i<=n;++i)h[i]=H[i-1];
for(int i=2;i<=n;++i)Log2[i]=Log2[i>>1]+1;
top=0;
for(int i=1;i<=n;++i){
while(top&&h[stac[top]]<h[i])--top;
if(top)high[i][0]=stac[top],lft[i][0]=stac[top];
stac[++top]=i;
}
top=0;
for(int i=n;i>=1;--i){
while(top&&h[stac[top]]<h[i])--top;
if(top)high[i][0]=maxx(high[i][0],stac[top]),rght[i][0]=stac[top];
stac[++top]=i;
}
for(int i=1;(1<<i)<=n;++i)
for(int j=1;j<=n;++j)
high[j][i]=high[high[j][i-1]][i-1],rght[j][i]=rght[rght[j][i-1]][i-1],lft[j][i]=lft[lft[j][i-1]][i-1];
for(int i=1;i<=n;++i)st[i][0]=h[i];
for(int i=1;(1<<i)<=n;++i)
for(int j=1;j+(1<<i)-1<=n;++j)
st[j][i]=max(st[j][i-1],st[j+(1<<(i-1))][i-1]);
}
int minimum_jumps(int A,int B,int C,int D){
++A;++B;++C;++D;
int a=query(B+1,C),b=query(C,D);
if(a>b||h[B]>b)return -1;
int pos=B;
for(int i=Log2[B-A+1];~i;--i)
if(lft[pos][i]&&lft[pos][i]>=A&&h[lft[pos][i]]<=b)pos=lft[pos][i];
if(lft[pos][0]&&lft[pos][0]>=A&&h[lft[pos][0]]<=b)pos=lft[pos][0];
if(h[pos]>=a)return 1;
int ans=0;
for(int i=Log2[n];~i;--i)
if(high[pos][i]&&h[high[pos][i]]<a)pos=high[pos][i],ans+=(1<<i);
int mn=inf;
if(high[pos][0]&&h[high[pos][0]]>a&&h[high[pos][0]]<=b)mn=ans+2;
for(int i=Log2[n];~i;--i)
if(rght[pos][i]&&rght[pos][i]<C)pos=rght[pos][i],ans+=(1<<i);
return min(mn,ans+1);
}
T3 封闭道路 roads
题意
给定一棵树,每条边有边权,对于所有\(0\le k\le n-1\),计算使得所有点的度数都\(\le k\),需要断掉的边的最小边权之和。
数据范围:\(n\le 10^5\)
solution
首先考虑暴力树形DP,对每一种度数分别考虑
记\(f_{u,0/1}\)表示与父亲的边不删/删的最小代价。那么如果不考虑度数限制,那么\(f_{u,0/1}=\sum_v\min(f_{v,0},f_{v,1}+w)\)。如果有一些\(f_{v,1}+w\le f_u\)(称其为好点),那当然好了,肯定贪心的先把他们选完。把剩下的\(f_{v,0}-(f_{v,1}+w)\)放进堆里边,选择代价最小的几个求和。
我们发现,如果一个点的度数\(<\)当前需要考虑的度数,那么这个点\(f_{u,0/1}=0\),而且肯定不是好点。所以我们可以直接把它扔进与它有边相连的顶点的堆中。依然对每一个度数单独考虑,我们每次DP的时候,如果一个儿子的度数\(\ge\)当前在计算的度数,像暴力一样树形DP即可,加入堆中即可。
因为插入堆中之后还要删除,我们需要一个支持删除的堆(或者一个平衡树)。具体的,对于每个要被删除的元素也维护一个堆,如果当前的大堆的堆顶元素与需要被删除的堆的堆顶元素相同,同时将这两个堆顶删去。
因为所有点的度数之和是\(O(n)\)的,所以复杂度是\(O(n\log n)\)。注意要将儿子、所有顶点按照度数排序,否则复杂度是错误的。
#include <bits/stdc++.h>
using namespace std;
const int N=250005;
#define pb push_back
#define pr pair<int,int>
#define mp make_pair
vector<pr> e[N];
int deg[N];
inline void adde(int u,int v,int w){
e[u].pb(mp(v,w));++deg[u];
e[v].pb(mp(u,w));++deg[v];
}
int id[N];
inline bool cmp(int a,int b){return deg[a]<deg[b];}
inline bool cmp2(pr a,pr b){return deg[a.first]>deg[b.first];}
int n;
#define ll long long
struct Heap{
priority_queue<ll> q,del;
int sz;ll sum;
inline void init(){
while(!q.empty())q.pop();
while(!del.empty())del.pop();
sz=sum=0;
}
inline void push(ll x){++sz;sum+=x;q.push(x);}
inline void erase(ll x){--sz;sum-=x;del.push(x);}
inline void update(){
while(!q.empty()&&!del.empty()&&q.top()==del.top())q.pop(),del.pop();
}
inline ll top(){update();return q.top();}
inline void pop(){--sz;sum-=top();q.pop();}
inline bool empty(){return sz<=0;}
}q[N];
int cur;
inline void del(int u){
for(pr i:e[u]){
int v=i.first,len=i.second;
if(deg[v]<=cur)break;
q[v].push(len);
}
}
int vis[N];
ll f[N][2];
ll stac[N],top;
inline void undo(int u){while(top)q[u].push(stac[top--]);}
void dfs(int u,int fa){
vis[u]=cur;f[u][0]=f[u][1]=0;
for(pr i:e[u]){
int v=i.first;
if(v==fa)continue;
if(deg[v]<=cur)break;
dfs(v,u);
}
top=0;
int cnt=deg[u]-cur;ll sum=0;
while(!q[u].empty()&&q[u].sz>cnt)q[u].pop();
for(pr i:e[u]){
int v=i.first,len=i.second;
if(v==fa)continue;
if(deg[v]<=cur)break;
if(f[v][1]+len<=f[v][0]){
--cnt;
sum+=f[v][1]+len;
}else{
sum+=f[v][0];
q[u].push(f[v][1]+len-f[v][0]);
while(!q[u].empty()&&q[u].sz>cnt)stac[++top]=q[u].top(),q[u].pop();
}
}
while(!q[u].empty()&&q[u].sz>cnt)stac[++top]=q[u].top(),q[u].pop();
f[u][0]=sum+q[u].sum;
while(!q[u].empty()&&q[u].sz>cnt-1)stac[++top]=q[u].top(),q[u].pop();
f[u][1]=sum+q[u].sum;
undo(u);
for(pr i:e[u]){
int v=i.first,len=i.second;
if(v==fa)continue;
if(deg[v]<=cur)break;
if(f[v][1]+len>f[v][0])
q[u].erase(f[v][1]+len-f[v][0]);
}
}
vector<ll> minimum_closure_costs(int NN,vector<int> U,vector<int> V,vector<int> W){
n=NN;ll sum=0;
for(int i=1,u,v,w;i<n;++i){
u=U[i-1]+1;v=V[i-1]+1;w=W[i-1];
adde(u,v,w);
sum+=w;
}
for(int i=1;i<=n;++i)id[i]=i,sort(e[i].begin(),e[i].end(),cmp2);
sort(id+1,id+1+n,cmp);
int flag=1;
vector<ll> ret;
ret.pb(sum);
for(cur=1;cur<n;++cur){
while(flag<=n&°[id[flag]]<=cur)del(id[flag]),++flag;
ll ans=0;
for(int i=flag,u;i<=n;++i){
u=id[i];
if(vis[u]!=cur){
dfs(u,0);
ans+=f[u][0];
}
}
ret.pb(ans);
}
return ret;
}


