多项式模板

多项式乘法

多项式表示方法

以下的多项式长度为\(n\)，即最高次数为\(n-1\)，共\(0,1,\cdots n-1\)，\(n\)位多项式

系数表示法

即最常见的表示方法：

\[f(x)=a_0+a_1x+a_2x^2+\cdots a_{n-1}x^{n-1}=\sum\limits_{i=0}^{n-1}a_ix^i \]

存储时只存每一位的系数即可

\[f(x)=\{a_0,a_1,a_2,\cdots,a_{n-1}\} \]

点值表示法

即把多项式放到平面直角坐标系内，得到一个函数图像

把\(n\)个不同的\(x\)带入，得到\(n\)个\(y\)

\[f(x)=\{(x_0,f(x_0)),(x_1,f(x_1)),(x_2,f(x_2)),\cdots,(x_{n-1},f(x_{n-1}))\} \]

---

系数表示法是最常见的一种表示法，而点值表示法是最方便的一种表示法

系数表示法的方便之处不用多说，简单说一下点值表示法的好处：

计算多项式乘法时：点值表示法可以\(O(n)\)求，即对应每一位乘起来即可

\[f(x) \cdot g(x)=\{(x_0,f(x_0)g(x_0),(x_1,f(x_1)g(x_1),\cdots (x_{n-1},f(x_{n-1})g(x_{n-1})\} \]

这两种表示法可以相互转化。但是暴力转化的话，系数转点值是\(O(n^2)\)的

那么就需要用到下面的两种办法来解决一下，把时间优化到\(O(n\log n)\)

快速傅里叶变换 FFT

上面说过，对于任意系数多项式转点值，当然可以随便取任意\(n\)个\(x\)值代入计算，但是时间为\(O(n^2)\)

那么考虑找一些\(x\)值使得\(x^n=1\)，这样\(n\)次方后就会出现循环，就不用做全部的\(n\)次方运算了

但是这样的\(x\)只有\(\pm 1\)，那么需要考虑把它弄到复数域去

复数

定义\(i^2=-1\)，用\(z=a+bi\)表示复数。\(a\)称为实部，\(b\)称为虚部。\(z'=a-bi\)称为\(z\)的共轭复数（即虚部取反）

运算法则（\(z_1=a+bi,z_2=c+di\)）：

• \[z_1+z_2=(a+c)+(b+d)i \]

• \[z_1\cdot z_2=(ac-bd)+(ad+bc)i \]

struct Complex{double a,b;Complex(double xx=0,double yy=0){a=xx,b=yy;}}
inline Complex operator+(Complex x,Complex y){x.a+=y.a;x.b+=y.b;return x;}
inline Complex operator-(Complex x,Complex y){x.a-=y.a;x.b-=y.b;return x;}
inline Complex operator*(Complex x,Complex y){return Complex(x.a*y.a-x.b*y.b,x.a*y.b+x.b*y.a);}

---

回到正题

有一个\(x\)轴为实部，\(y\)轴为虚部的坐标轴。作一个以原点为圆心，\(1\)为半径的单位圆

使得\(x^n=1\)的\(x\)一定在这个圆上，即把这个圆\(n\)等分，得到的交点。理解一下：把这个角度乘上\(n\)倍一定与\(x\)轴正方向重合

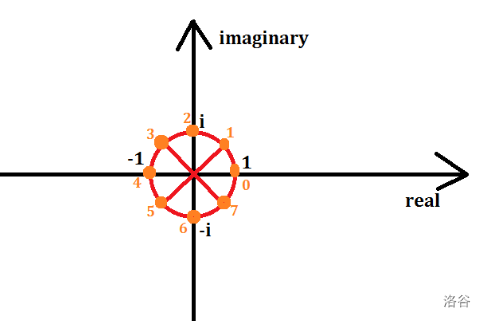
设这个交点为$ \omega_n^{k$（分成$n$份，$\omega_n$的$k$次方），$\omega_n}k$为单位根

\[\omega_n^k=\cos \frac{k}{n}2\pi+\sin\frac{k}{n}2\pi\cdot i \]

结合这个图理解一下

单位根的性质

1. \[\omega_n^k=\omega_{2n}^{2k}=\omega_{mn}^{mk} \]

直接带定义式即可证明

2. \[\omega_n^{k+\frac{n}{2}}=-\omega_n^k \]

3. \[\omega_n^0=\omega_n^n=1 \]

终于到了FFT的时间

\[f(x)=(a_0+a_2x^2+\cdots+a_{n-2}x^{n-2})+x(a_1+a_3x^2+\cdots x_{n-1}x^{n-2}) \]

令\(f_1(x)=a_0+a_2x+a_4x^2+\cdots+a_{n-2}^{\frac{n}{2}-1}\),\(f_2(x)=a_1+a_3x+a_5x^2+\cdots+a_{n-1}^{\frac{n}{2}-1}\)

则\(f(x)=f_1(x)+xf_2(x)\)

带入\(\omega_n^k\)得

\[f(\omega_n^k)=f_1(\omega_n^{2k})+\omega_n^kf_2(\omega_n^{2k})=f_1(\omega_\frac{n}{2}^k)+\omega_n^kf_2(\omega_\frac{n}{2}^k) \]

带入\(\omega_n^{k+\frac{n}{2}}=-\omega_n^k\)得

\[f(\omega_n^{k+\frac{n}{2}})=f_1(\omega_n^{2k})-\omega_n^kf_2(\omega_n^{2k})=f_1(\omega_\frac{n}{2}^k)-\omega_n^kf_2(\omega_\frac{n}{2}^k) \]

所以求出\(f(\omega_n^k)\)的同时可以求出\(f(\omega_n^{k+\frac{n}{2}})\)，把一个\(n\)优化到了\(\log n\)

注意FFT必须令多项式的长度为\(2\)的整数次方，否则多加几位0使它等于\(2\)的整数次方位

while(len<=n+m)len<<=1,++cnt;

递归求解即可

但是递归的常数巨大，考虑直接把每个数直接交换到相应的位置上

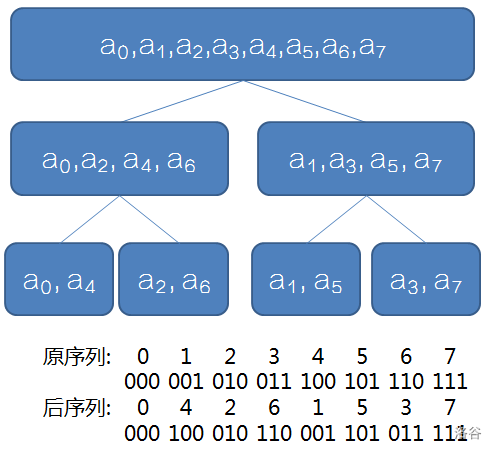
可以发现：交换后序列的位置为 交换前序列的二进制下 翻转过来

for(int i=0;i<len;++i)	pos[i]=(pos[i>>1]>>1)|((i&1)<<(cnt-1));

解释一下这个的含义：把自己的最后一位去掉（i>>1），翻转（pos[i>>1]>>1，即去掉自己的最后一位反转的结果多了一位\(0\)，把这个\(0\)去掉），再把最后一位弄上去（((i&1)<<(cnt-1))）

再结合一个例子：已知\(00101\)翻转为\(10100\)，再求\(01011\)翻转后的值

去掉最后一位（第一位补\(0\)）：\(00101\)，翻转\(10100\)，去掉最后一位\(01010\)，原来的最后一位补上去\(11010\)

得到了应该放到的位置后交换：

for(int i=0;i<len;++i)if(i<pos[i])swap(f[i],f[pos[i]]);\

这个if必须要有，不然要来回交换两次，相当于没动

inline void FFT(Complex *f){
	for(int i=0;i<len;++i)	if(i<pos[i])swap(f[i],f[pos[i]]);
	for(int mid=1;mid<len;mid<<=1){
		Complex base=Complex(cos(Pi/mid),sin(Pi/mid));
		for(int j=0;j<len;j+=(mid<<1)){
			w=Complex(1,0);
			for(int k=j;k<j+mid;++k,w=w*base){
				Complex x=f[k],y=w*f[k+mid];
				f[k]=x+y;f[k+mid]=x-y;
			}
		}	
	}
}

至此我们完成了 系数表示法 转 点值表示法

IFFT（快速傅里叶逆变换）

现在我们需要完成 点值表示法 转 系数表示法

把\(\omega_n^k\)换成其的共轭复数，再对其系数都除以\(len\)（\(len\)为\(2^k\)）

证明如下：

\(\omega_n^k\)的共轭复数=\(\omega_n^{-k}\)，根据三角函数的性质可以得到\(\cos(-x)=\cos x,\sin(-x)=-\sin x\)，带回单位根的定义式即可

现在我们已经得到了一个函数\(f(x)\)在\(\omega_n^0,\omega_n^1,\cdots,\omega_n^{n-1}\)的点值\(g(x)\)，设为\(y_0,y_1,\cdots,y_{n-1}\)，求出原函数\(f(x)\)的各项系数\(f_0,f_1,\cdots,f_{n-1}\)

\[g(x)=\sum\limits_{i=0}^{n-1}y_ix^i,y_i=\sum\limits_{j=0}^{n-1}f_j(\omega_n^i)^j \]

代入得

\[g(x)=\sum\limits_{i=0}^{n-1}\sum\limits_{j=0}^{n-1}f_j(\omega_n^i)^jx^i \]

把\(\omega_n^{-k}\)作为\(x\)代入

\[g(x)=\sum\limits_{i=0}^{n-1}\sum\limits_{j=0}^{n-1}f_j(\omega_n^i)^{j-k}=\sum\limits_{j=0}^{n-1}f_j\sum\limits_{i=0}^{n-1}(\omega_n^{j-k})^i \]

令\(S(x)=\sum\limits_{i=0}^{n-1}(\omega_n^{x})^i\)，则有\(\omega_n^x S(x)=\sum\limits_{i=0}^{n-1}(\omega_n^{x})^i\)

两式相减得

\[S(x)=\dfrac{(\omega_n^x)^n-(\omega_n^x)^0}{\omega_n^x-1}=\dfrac{(\omega_n^n)^x-1}{\omega_n^x-1}=\dfrac{1-1}{\omega_n^x-1}=\dfrac{0}{\omega_n^x-1} \]

当\(\omega_n^x=1(x<n)\)时，即\(x=0\)时，\(S(0)=\sum_{i=0}^{n-1}1^i=n\)，否则该式\(=0\)

带回原式

\[g(\omega_n^{-k})=\sum\limits_{j=0}^{n-1}f_jS(j-k) \]

当\(j=k\)时\(S(j-k)=n\)，其余时候\(S(j-k)=0\)

那么

\[g(\omega_n^{-k})=nf_j \]

所以对当前已知点值表示法的\(g(x)\)代入\(\omega_n^{-k}\)，再除以\(n\)，即可得到系数表示法的\(f(x)\)

inline void FFT(Complex *f,int flag){
	for(int i=0;i<len;++i)	if(i<pos[i])swap(f[i],f[pos[i]]);
	for(int mid=1;mid<len;mid<<=1){
		Complex base=Complex(cos(Pi/mid),flag*sin(Pi/mid));//取-1即为点值转系数
		for(int j=0;j<len;j+=(mid<<1)){
			w=Complex(1,0);
			for(int k=j;k<j+mid;++k,w=w*base){
				Complex x=f[k],y=w*f[k+mid];
				f[k]=x+y;f[k+mid]=x-y;
			}
		}	
	}
}

主函数中

while(len<=n+m)	len<<=1,++cnt;
for(int i=0;i<len;++i)	pos[i]=(pos[i>>1]>>1)|((i&1)<<(cnt-1));
FFT(a,1);FFT(b,1);
for(int i=0;i<len;++i)	a[i]=a[i]*b[i];
FFT(a,-1);
for(int i=0;i<=n+m;++i)printf("%.0lf ",(a[i].a+0.5)/len);//注意精度

快速数论变换 NTT

FFT的精度会爆炸（\(\sin,\cos\)当然了），我们需要一种精度更高的做法

阶

若\(a,p\)互素，且\(p>1\)，

对于\(a^n≡1\pmod p\)最小的\(n\)，我们称之为\(a\)模\(p\)的阶,记做\(δ_p(a)\)

例如：\(δ_7(2)=3\)

原根

设\(p\)是正整数，\(a\)是整数，若\(δ_p(a)\)等于\(ϕ(p)\)，则称\(a\)为模\(p\)的一个原根，记为\(g\)

\(δ_7(3)=6=ϕ(7)\)，因此\(3\)是模\(7\)的一个原根

注意原根的是不唯一的

于是可以得到一个结论

\[\omega_n\equiv g^\frac{p-1}{n} \pmod p \]

用这个可以代替FFT中的单位根\(\omega\)，因为它满足FFT中虚数\(\omega\)的全部性质（模意义下）

证明（以下等号均表示在\(\mod p\)意义下同余）：

• 性质\(1\)：\(\omega_n^0=\omega_n^n=1\)

显然 \(\omega_n^0=g^0=1\)，\(\omega_n^n=g^{p-1}\)

根据费马小定理\(g^{p-1}\equiv 1 \pmod{p}\)，得证

• 性质\(2\)：\(\omega_{2n}^{2k}=\omega_n^k\)

直接代定义式得：\(\omega_{2n}^{2k}=(g^{\frac{p-1}{2n}})^{2k}=g^{\frac{2k\cdot(p-1)}{2n}}=g^{\frac{k\cdot(p-1)}{n}}=(g^{\frac{p-1}{n}})^k=\omega_n^k\)

• 性质\(3\)：\(\omega_{n}^{k+\frac{n}{2}}=-\omega_n^k\)

\[(\omega_n^{\frac{n}{2}})^2=g^{p-1}\equiv1\pmod p \]

\[\omega_n^{\frac{n}{2}}\equiv\pm1\pmod p \]

补充一条原根的性质：

若\(P\)为素数，那么原根\(g^i\mod p\) \((\forall i \in (0,P)\cap N_{\ast})\)的结果两两不同

那么\(\omega_n^{\frac{n}{2}}\ne \omega_n^{n},\omega_n^n=1\)，那么\(\omega_n^{\frac{n}{2}}\equiv -1 \pmod p\)

那么\(\omega_n^{k+\frac{n}{2}}=\omega_n^k\cdot\omega_n^{\frac{n}{2}}=-\omega_n^k\)，得证

---

即把FFT中的\(\omega_n^k=\cos \frac{k}{n}2\pi+\sin\frac{k}{n}2\pi\cdot i\)替换为 \(g^{k\times\frac{p-1}{n}}\mod p\)即可

原根没什么快速求法，只能暴力枚举判断
通常模数常见的有\(998244353 , 1004535809,469762049\)。这几个的原根都是\(3\)

还原的话取\(g^{-\frac{p-1}{n}}\)，即\(inv(g)^\frac{p-1}{n}\)即可

顺便加上封装，代码如下

const int mod=998244353,G=3,N=(1<<21)+10;
namespace Math{
	int inv[N],pos[N],curmx;
	inline int add(int a,int b){return (a+b>=mod)?a+b-mod:a+b;}
	inline int dec(int a,int b){return (a-b<0)?a-b+mod:a-b;}
	inline int mul(int a,int b){return 1ll*a*b%mod;}
	inline int quick_pow(int a,int b){int ret=1;for(;b;b>>=1,a=mul(a,a))if(b&1)ret=mul(a,ret);return ret;}
	inline int Inv(int a){return quick_pow(a,mod-2);}
	int invg=Inv(G);
	inline int init_pos(int n){
		int len=1,cnt=0;while(len<=n)len<<=1,++cnt;
		for(int i=0;i<len;i++)pos[i]=(pos[i>>1]>>1)|((i&1)<<(cnt-1));
		return len;
	}
}
using namespace Math;
struct poly{
	vector<int> v;
	inline int& operator[](int a){while(a>=v.size())v.push_back(0);return v[a];}//取第x位，若不足则补0
	inline void clear(int a,int b){for(int i=a;i<b;++i)v[i]=0;}
}f,g;
namespace Basic{
	inline void Read(int n,poly &f){for(int i=0;i<n;++i)f[i]=read();}//读入
	inline void Print(int n,poly f){for(int i=0;i<n;++i)printf("%d ",f[i]);puts("");}//输出
	inline void cpy(int n,poly &f,poly f1){for(int i=0;i<n;++i)f[i]=f1[i];}
	inline void NTT(poly &f,int len,int flag){
		for(int i=0;i<len;i++)if(i<pos[i])swap(f[i],f[pos[i]]);
		for(int mid=1;mid<len;mid<<=1){
			int base=quick_pow((flag==1)?G:invg,(mod-1)/(mid<<1));
			for(int i=0,w=1;i<len;i+=(mid<<1),w=1)
				for(int j=i;j<i+mid;++j,w=mul(w,base)){
					int x=f[j],y=mul(w,f[j+mid]);
                    f[j]=add(x,y),f[j+mid]=dec(x,y);
				}
		}
	}
	inline void Mul(poly &a,poly b,int n,int m){
		int len=init_pos(n+m);init_inv(len);
		NTT(a,len,1);NTT(b,len,1);for(int i=0;i<len;++i)a[i]=mul(a[i],b[i]);
		NTT(a,len,-1);int invn=inv[len];
		for(int i=0;i<len;i++)a[i]=mul(a[i],invn);//还原
	}
}
using namespace Basic;
int n,m;
int main(){
	n=read()+1;m=read()+1;
	Read(n,f);Read(m,g);
	Mul(f,g,n,m);Print(n+m-1,f);
	return 0;
}

其余的相关计算多项式运算

多项式乘法逆

已知\(f(x)\)，求\(g(x)\)使得\(f(x)\cdot g(x)\equiv1\pmod{x^n}\)

考虑递归求解

假设我们已经求出\(h(x)\)，使得\(h(x)\cdot f(x)\equiv1\pmod{x^{\left\lceil\frac{n}{2}\right\rceil}}\)，现在要求\(g(x)\cdot f(x)\equiv1\pmod{x^n}\)

那么显然\(g(x)\cdot f(x)\equiv 1 \pmod{x^{\left\lceil\frac{n}{2}\right\rceil}}\)

两式相减得

\[f(x)\cdot(h(x)-g(x))\equiv 0 \pmod{x^{\left\lceil\frac{n}{2}\right\rceil}} \]

即

\[h(x)-g(x)\equiv 0 \pmod{x^{\left\lceil\frac{n}{2}\right\rceil}} \]

两边平方得

\[h(x)^2-2h(x)g(x)+g(x)^2\equiv 0 \pmod{x} \]

两边同时乘以\(f(x)\)

\[f(x)\cdot h(x)^2-2f(x)h(x)g(x)+f(x)\cdot g(x)^2\equiv 0 \pmod{x} \]

根据\(f(x)g(x)\equiv 1 \pmod{x}\)

\[f(x)\cdot h(x)^2-2h(x)+g(x)\equiv 0\pmod{x} \]

移项得结论：

\[g(x)\equiv 2h(x)-f(x)h(x)^2 \]

边界条件：\(n=1\)时，\(g(0)\cdot f(0)\equiv1\pmod x\)，取\(g(0)=inv(f(0))\)

直接NTT即可

注意代码的一些细节

1. \(g(x)\)在\(\mod x^n\) 意义下，所以次数\(\ge n\)的位系数均为\(0\)

2. 代入公式时，先把\(h(x),f(x)\)NTT一遍得到点值表示，直接进行乘、减运算，这样得到的仍然是一个点值表示，再NTT一遍转回系数表示

poly Get_inv(poly f,int n){//求逆 
	poly g;
	if(n==1){g[0]=Inv(f[0]);return g;}
	g=Get_inv(f,(n+1)>>1);
	int len=init_pos(n<<1);
	poly a;cpy(n,a,f);
	NTT(a,len,1);NTT(g,len,1);
	for(int i=0;i<len;++i)g[i]=mul(dec(2,mul(a[i],g[i])),g[i]);
	NTT(g,len,-1);int invn=Inv(len);
	for(int i=0;i<len;++i)g[i]=(i<n)?mul(g[i],invn):0;
	return g;
}

多项式对数函数（多项式ln）

已知多项式\(A(x)\)，求\(B(x)\)使得\(B(x)\equiv \ln A(x)\pmod{x^n}\)

保证\(a_0=1\)

前置芝士：

求导

大概就是求函数上某个点的斜率，用\(f'(x)\)表示\(f(x)\)的导函数，用\(f^{(i)}\)表示\(f(x)\)的\(i\)阶导

常用公式

1. \[(u(x)\pm v(x))'=u'(x)\pm v'(x) \]

\[(u(x)\cdot v(x))'=u'(x)v(x)+u(x)+v'(x) \]

\[\left(\dfrac{u(x)}{v(x)}\right) '=\dfrac{u'(x)v(x)-v'(x)u(x)}{v^2(x)} \]

同时这三个公式都可以推广到\(n\)个

2. \[(x^n)'=nx^{n-1} \]

那么结合上述两个公式可以得到

对于\(f(x)\)求导，即对每一位求导再加起来。\(f(x)\)的第\(i\)次：\(f_ix^i\)求导得\(if_ix^{i-1}\)

那么\(f'(x)=\sum\limits_{i=1}^{n-1}if_ix^{i-1}\)，\(f'(x)\)的第\(n-1\)次项系数为\(0\)

代码

inline poly derive(poly f,int n){
	poly ret;
    for(int i=1;i<n;++i)ret[i-1]=mul(f[i],i);
    return ret;
}//求导 

3. 复合函数求导

\(y(x)=f(g(x))\)，则

\[y'(x)=f'(g(x))\cdot g'(x) \]

4. 特殊函数求导

\[(\ln x)'=\dfrac{1}{x} \]

积分

即求导的逆运算

inline poly interg(poly f,int n){
	poly ret;
    for(int i=1;i<n;++i)ret[i]=mul(f[i-1],Inv(i));
    return ret;
}//积分

---

回到正题

令\(f(x)=\ln x\)，则

\[B(x)\equiv f(A(x))\pmod{x^n} \]

两边求导得

\[B'(x)\equiv f'(A(x))A'(x)\pmod{x^n} \]

根据\((\ln x)'=\dfrac{1}{x}\)

\[B'(x)\equiv \dfrac{A'(x)}{A(x)}\pmod{x^n} \]

然后积分积回去即可

\[B(x)\equiv\int\dfrac{A'(x)}{A(x)} \]

inline poly Get_ln(poly f,int n){//对数函数 
	poly der=derive(f,n);//求导
   	poly g=Mul(der,Get_inv(f,n),n,n);//除法（乘上逆）
	return interg(g,n);//积回去
}

多项式牛顿迭代

前置芝士

泰勒展开

将一个在\(x=x_0\)处具有\(n\)阶导数的函数\(f(x)\)利用关于\((x-x_0)\)的\(n\)次多项式来逼近函数

当然这个\(n\)越大，函数就越逼近

成立下式：

\[f(x)=\sum\limits_{i=0}^{\infty}\dfrac{f^{(i)}(x_0)}{i!}(x-x_0)^i \]

其中\(f^{(i)}\)表示\(f(i)\)的\(i\)阶导

---

已知\(f(x)\)，求\(g(x)\)使\(f(g(x))\equiv 0\pmod{n^n}\)

类似倍增

假设已经求出了\(g_0(x)\)满足\(f(g_0(x))\equiv 0\pmod{x^{\left\lceil\frac{n}{2}\right\rceil}}\)

在\(g_0(x)\)处进行泰勒展开

\[f(g_0(x))=\sum\limits_{i=0}^{\infty}\dfrac{f^{(i)}(g_0(x))}{i!}(g(x)-g_0(x))^i \]

因为\(f(g(x))\equiv 0\pmod{n^n}\)，\(f(g_0(x))\equiv 0\pmod{x^{\left\lceil\frac{n}{2}\right\rceil}}\)

那么\(g_0(x)\)和\(g(x)\)的最后\(\left\lceil\frac{n}{2}\right\rceil\)位必须相同

即

\[g(x)-g_0(x)\equiv 0\pmod {x^{\left\lceil\frac{n}{2}\right\rceil}} \]

那么\(\forall i\ge 2\)

\[g(x)-g_0(x)\equiv 0\pmod x \]

那么上面的泰勒展开式中\(i\ge 2\)的\((g(x)-g_0(x))^i\)都为\(0\)，也就是说只有\(i=0,1\)的两项

把这两项展开得

\[f(g(x))\equiv f(g_0(x))+f'(g_0(x))(f(x)-g_0(x))\pmod{x^n} \]

移项

\[f'(g_0(x))g(x)+f(g_0(x))-f'(g_0(x))g_0(x)\equiv 0 \pmod {x^n} \]

\[g(x)\equiv g_0(x)-\dfrac{f(g_0(x))}{f'(g_0(x))} \pmod {x^n} \]

\(n=1\)时需要特判边界

这样往下迭代即可

多项式指数函数（多项式 exp）

已知\(f(x)\)，求\(g(x)\)满足\(g(x)\equiv e^{f(x)}\pmod{x^n}\)

保证\(a_0=0\)

两边取\(\ln\)得

\[\ln g(x)\equiv f(x)\pmod{x^n} \]

\[\ln g(x)-f(x)\equiv 0\pmod{x^n} \]

代入刚才的牛顿迭代式

\[g(x)\equiv g_0(x)-\dfrac{\ln g_0(x)-f(x)}{\frac{1}{g_0(x)}}\pmod{x^n} \]

\[\equiv g_0(x)(1-\ln g_0(x)+f(x))\pmod{x^n} \]

递归即可

边界（\(n=1\)）：因为题目保证\(f(x)\)常数项为\(0\)，那么\(\ln g(x)=0\)，即\(g(x)=1\)

poly Get_exp(poly f,int n){//指数函数 
	poly g;if(n==1){g[0]=1;return g;}
	g=Get_exp(f,(n+1)>>1),n;poly a=Get_ln(g,n);
	for(int i=0;i<n;i++)a[i]=add((i==0),dec(f[i],a[i]));
	return Mul(g,a,n,n);
}

多项式除法

已知\(n-1\)次多项式\(f(x)\)和一个\(m-1\)次多项式\(g(x)\)，求多项式\(Q(x)\),\(R(x)\)

• \(Q(x)\)为商，\(R(x)\)为余数
• \(Q(x)\)次数为\(n-m\)，\(R(x)\)次数小于\(m-1\)（暂且令其为\(m-2\)次）

只要我们把\(Q(x)\)找出来了，那么\(f(x)-g(x)Q(x)\)即可得到\(R(x)\)

设\(h_r(x)\)表示翻转\(h(x)\)的各项系数后的函数

inline void rev(poly &f,int n){reverse(f.v.begin(),f.v.begin()+n);}

这个满足\(h_r(x)=x^{n-1}h(\dfrac1x)\)

来推式子（下面式子除说明外，\(=\)表示\(\mod x^n\)意义下相等）

\[f(x)=Q(x)\cdot g(x)+r(x) \]

\[f(\frac1x)=Q(\frac1x)\cdot g(\frac1x)+r(\frac1x) \]

两边同时乘上\(x^{n-1}\)

\[x^{n-1}f(\frac1x)=x^{n-m}Q(\frac1x)\cdot x^{m-1}g(\frac1x)+x^{n-m+1}\cdot x^{m-2}R(\frac1x) \]

这里的次数分配有助于下一步化简

转换为\(h_r\)形式

\[f_r(x)\equiv Q_r(x)\cdot g_r(x)+x^{n-m+1}R_r(x)\pmod{x^{n-m+1}} \]

\[f_r(x)\equiv Q_r(x)\cdot g_r(x)\pmod{x^{n-m+1}} \]

\[Q_r(x)\equiv f_r(x)\cdot g_r^{-1}(x)\pmod{x^{n-m+1}} \]

求出\(g_r(x)\)的逆，再乘上\(f_r(x)\)即可得到\(Q_r(x)\)。再reverse回去即可得到\(Q(x)\)

\(R(x)=f(x)-g(x)Q(x)\)求得\(R(x)\)

注意式子最后一步是在\(\mod {x^{n-m+1}}\)意义下的，那么\(f,g\)中次数高于\(n-m\)的部分不需要，这样可以减小一点常数吧

poly div(poly f,poly g,int n,int m){//被除数 除数 求商 
	rev(f,n);rev(g,m);g.clear(n-m+1,m);f.clear(n-m+1,n);g=Get_inv(g,n-m+1);
	poly ret=Mul(f,g,n-m+1,n-m+1);ret.clear(n-m+1,2*(n-m+1));
	rev(ret,n-m+1);return ret;
}
poly Get_mod(poly f,poly g,poly h,int n,int m){//被除数 除数 商 求余数 
	g=Mul(g,h,m,n-m+1);
	for(int i=0;i<m-1;++i)f[i]=dec(f[i],g[i]);
	return f;
}

多项式开根

前置芝士：

二次剩余（Cipolla算法）

若存在\(x\)使得\(x^2\equiv n\pmod p\)，则称\(n\)为\(\mod p\) 的二次剩余

勒让德符号

\[\left(\dfrac{n}{p}\right)=\begin{cases}1\ p\nmid n \text{且$n$是$p$的二次剩余}\\-1\ p\nmid n \text{且$n$不是$p$的二次剩余}\\0\ p\mid n\end{cases} \]

欧拉判别准则

\[\left(\dfrac{n}{p}\right)\equiv n^{\frac{p-1}{2}}\pmod p \]

有\(\dfrac{p-1}{2}\)个数是\(\mod p\) 意义下的二次非剩余

那么随机一个\(a\in[0,p)\)，令\(\omega^2\equiv a^2-n\pmod p\)。根据欧拉判别准则判断一下\(\omega\)是不是\(p\)的二次非剩余，找到一个\(p\)的二次非剩余\(\omega\)

找到这个\(a\)的期望次数是\(2\)

有结论：

\[x\equiv (a+\omega)^{\frac{p+1}2}\pmod p \]

证明

两边平方：

\[x^2\equiv (a+\omega)^{p+1} \pmod p \]

\[\because (a+b)^p\equiv a^p+b^p\pmod p \]

\[\therefore x^2\equiv(a+\omega)^p(a+\omega)\equiv(a^p+\omega^p)(a+\omega)\pmod p \]

根据费马小定理\(a^p\equiv a^{p-1}\cdot a\equiv a\pmod p\)

\(\omega^p\equiv\omega(\omega^2)^{\frac{p-1}{2}}\equiv \omega(a^2-n)^{\frac{p-1}{2}}\equiv -\omega\pmod p\)

带回去得

\[(a-\omega)(a+\omega)\equiv a^2-\omega^2\equiv n\pmod p \]

得证

那代码该怎么写？

类似虚数的东西，已知\(\omega^2\)，求\((a+\omega)^{\frac{p+1}2}\)

设\(x=a+b\omega\)，则\(x_1x_2=(a_1+b_1\omega)(a_2+b_2\omega)=(a_1a_2+b_1b_2\omega^2)+(a_1b_2+a_2b_1)\omega\)

重载一下运算符即可

最后\(x\)取实部\(a\)就好了

两个解之和一定是\(p\)，那么如果求出来的\(x>\dfrac p2\)，那么减回去就好了

这个是这道模板题的代码

struct Complex{int x,y;Complex(int xx,int yy){x=xx,y=yy;}};
inline Complex operator + (Complex a,Complex b){a.x=add(a.x,b.x),a.y=add(a.y,b.y);return a;}
inline Complex operator * (Complex a,Complex b){
	return Complex(add(mul(a.x,b.x),mul(a.y,1ll*b.y*w%mod)),add(mul(a.x,b.y),mul(a.y,b.x)));
}
inline Complex quick_pow(Complex a,int b){Complex ret(1,0);for(;b;b>>=1,a=a*a)if(b&1)ret=ret*a;return ret;}
inline int quick_pow(int a,int b){int ret=1;for(;b;b>>=1,a=mul(a,a))if(b&1)ret=mul(ret,a);return ret;}
inline int Euler(int a){return quick_pow(a,(mod-1)>>1);}
inline int Cipolla(int n){
	n%=mod;
	if(Euler(n)==mod-1)	return -1;
	int a;
	while(1){
		a=rand()%mod;w=dec(mul(a,a),n);
		if(Euler(w)==mod-1)break;
	}
	return quick_pow(Complex(a,1),(mod+1)>>1).x;
}
int T,n;
int main(){
	T=read();
	while(T--){
		n=read();mod=read();
		if(n==0){puts("0");continue;}
		int ans=Cipolla(n);
		if(ans==-1){puts("Hola!");continue;}
		if(ans>(mod>>1))ans=mod-ans;
		printf("%d %d\n",ans,mod-ans);
	}
	return 0;
}

封装一下方便多项式用

namespace Cipolla{
	struct Complex{int x,y;Complex(int xx,int yy){x=xx,y=yy;}};int w;
	inline Complex operator + (Complex a,Complex b){a.x=add(a.x,b.x),a.y=add(a.y,b.y);return a;}
	inline Complex operator * (Complex a,Complex b){return Complex(add(mul(a.x,b.x),mul(a.y,1ll*b.y*w%mod)),add(mul(a.x,b.y),mul(a.y,b.x)));}
	inline Complex comp_quick_pow(Complex a,int b){Complex ret(1,0);for(;b;b>>=1,a=a*a)if(b&1)ret=ret*a;return ret;}
	inline int Euler(int a){return quick_pow(a,(mod-1)>>1);}
	inline int cipolla(int n){
		n%=mod;int a;
		while(1){
			a=rand()%mod;w=dec(mul(a,a),n);
			if(Euler(w)==mod-1)break;
		}
		int ret=comp_quick_pow(Complex(a,1),(mod+1)>>1).x;
		return (ret>(mod>>1))?mod-ret:ret;
	}
}

---

回到正题

假设已知\(h(x)^2\equiv f(x)\pmod {x^{\left\lceil\frac{n}{2}\right\rceil}}\)，求\(g(x)^2\equiv f(x)\pmod {x^n}\)

\[g(x)-h(x)\equiv 0\pmod {x^{\left\lceil\frac{n}{2}\right\rceil}} \]

平方得

\[g(x)^2-2h(x)g(x)+h(x)^2\equiv 0 \pmod {x^n} \]

\(f(x)\equiv g(x)^2\pmod {x^n}\)代入得

\[f(x)-2h(x)g(x)+h(x)^2\equiv 0 \pmod {x^n} \]

移项

\[g(x)\equiv\dfrac{f(x)+h(x)^2}{2h(x)}\pmod {x^n} \]

边界条件：\(g_0^2\equiv f_0 \pmod x\)，用上述Cipolla算法求出二次剩余即可

poly Get_sqrt(poly f,int n){
	poly g;
	if(n==1){g[0]=cipolla(f[0]);return g;}
	g=Get_sqrt(f,(n+1)>>1);
	int len=init_pos(n<<1);
	poly a=Get_inv(g,n),b;cpy(n,b,f);
	NTT(b,len,1);NTT(a,len,1);NTT(g,len,1);
	for(int i=0;i<len;++i)	g[i]=mul(mul(add(b[i],mul(g[i],g[i])),a[i]),Inv(2));
	NTT(g,len,-1);int invn=Inv(len);
	for(int i=0;i<len;++i)	g[i]=(i<n)?mul(g[i],invn):0;
	return g;
}

多项式快速幂

已知\(f(x)\)，求\(g(x)\)，使得\(g(x)\equiv f^k(x)\pmod {x^n}\)

数据范围：\(n\le 10^5,1\le k\le 10^{10^5}\)

推式子

两边取对数

\[\ln g(x)\equiv k\cdot \ln f(x)\pmod{x^n} \]

再取指数

\[e^{\ln g(x)}\equiv e^{k\cdot \ln f(x)}\pmod{x^n} \]

\[g(x)\equiv e^{k\cdot \ln f(x)}\pmod{x^n} \]

但是\(f_0\)不一定等于\(1\)，那么\(\ln f(x)\)就没法用

设 \(k\mod (mod-1)=k_2\)（费马小定理\(a^p\equiv a\pmod {p}\)）

那么我们就强制把\(f_0\)转成\(1\)

可以把每一位都除以\(f_0\)，最后把系数都乘上\(f_0^k\)，但是可能有\(f_0\)等于\(0\)的情况，这时候没法除

那么我们就找到最后一位不为\(0\)的位，设这是第\(c+1\)位（即\(x^c\)位）

那么只有\(x^{k_2\cdot c}\)位才有系数，后面的系数为\(0\)的个数为\(k_2c\)位

那么就相当于把后面的\(c\)位移回去，再把剩下的系数除以现在的最后一位，这样把最后一位变成了\(1\)

然后再按照\(g(x)\equiv e^{k\cdot \ln f(x)}\pmod{x^n}\)做即可

最后把后面的\(k_2c\)位赋为\(0\)，把剩下的对应移回去即可

注意下面的细节：

• 要先判断\(0\)的位数会不会大于\(n\)，而且不能只判断取模以后的\(k_2\)，而是应该判断取模之前的\(k\)，如果全是\(0\)，那么直接输出
• \(k_2\)的模数必须是\(mod-1\)

poly qpow(poly f,int n,int k1,int k2,int c){
	poly ans;if(1ll*c*k2>=n||c>=n)return ans;
	int v=Inv(f[c]),b=quick_pow(f[c],k2);for(int i=c;i<n;++i)f[i]=mul(f[i],v);
	for(int i=0,j=c;j<n;++i,++j)ans[i]=f[j];
	ans=Get_ln(ans,n);
	for(int i=0;i<n;++i)ans[i]=mul(ans[i],k1);
	ans=Get_exp(ans,n);
	for(int i=0;i<c*k2;++i)f[i]=0;
	for(int i=c*k2,j=0;i<n;++i,++j)f[i]=mul(ans[j],b);//注意要乘回去
	return f;
}
//主函数中
n=read();scanf("%s",s+1);int len=strlen(s+1);Read(n,f);
int c=0;while(f[c]==0&&c<n)++c;
for(int i=1;i<=len;++i){
	k1=add(mul(10,k1),s[i]-'0'),k2=10ll*k2%(mod-1)+s[i]-'0',k2=(k2>=mod-1)?k2-mod+1:k2;
	if(1ll*k1*c>n&&!f[0]){for(int i=0;i<n;++i)printf("0 ");return 0;}//特判0的个数大于n
}
Print(n,qpow(f,n,k1,k2,c));

优质板子

以下代码经过大力卡常，不建议在考场上使用，平时抄板用一用就好了

const int mod=998244353,G=3,N=(1<<20)+10;
namespace Math{
	int inv[N]={1,1},pos[N],mx;
	inline int add(int a,int b){return (a+b>=mod)?a+b-mod:a+b;}
	inline int dec(int a,int b){return (a-b<0)?a-b+mod:a-b;}
	inline void Add(int &a,int b){a+=(a+b>=mod)?b-mod:b;}
	inline void Dec(int &a,int b){a-=(a<b)?b-mod:b;}
	inline int mul(int a,int b){return 1ll*a*b%mod;}
	inline int quick_pow(int a,int b){int ret=1;for(;b;b>>=1,a=mul(a,a))if(b&1)ret=mul(a,ret);return ret;}
	inline void init_inv(int n){
		mx=n;
		for(int i=2;i<=n;++i)inv[i]=dec(mod,mul(mod/i,inv[mod%i]));
	}
	inline int Inv(int a){if(a<=mx)return inv[a];else return quick_pow(a,mod-2);}
	inline void init_pos(int cnt,int len){
		for(int i=0;i<len;++i)pos[i]=(pos[i>>1]>>1)|((i&1)<<cnt);
	}
}
using namespace Math;
namespace Cipolla{
    struct Complex{int x,y;Complex(int xx,int yy){x=xx,y=yy;}};int w;
    inline Complex operator + (Complex a,Complex b){a.x=add(a.x,b.x),a.y=add(a.y,b.y);return a;}
    inline Complex operator * (Complex a,Complex b){return Complex(add(mul(a.x,b.x),mul(a.y,1ll*b.y*w%mod)),add(mul(a.x,b.y),mul(a.y,b.x)));}
    inline Complex comp_quick_pow(Complex a,int b){Complex ret(1,0);for(;b;b>>=1,a=a*a)if(b&1)ret=ret*a;return ret;}
    inline int Euler(int a){return quick_pow(a,(mod-1)>>1);}
    inline int cipolla(int n){
        int a;
        while(1){
            a=rand();w=dec(mul(a,a),n);
            if(Euler(w)==mod-1)break;
        }
        int ret=comp_quick_pow(Complex(a,1),(mod+1)>>1).x;
        return (ret>(mod>>1))?mod-ret:ret;
    }
}
#define vec vector<int> 
struct poly{
	vec v;
	inline poly(int w=0):v(1){v[0]=w;}
	inline poly(const vec&_f):v(_f){}
	inline int& operator[](int x){if(v.size()<=x)v.resize(x+1);return v[x];}
	inline void resize(int r){v.resize(r);}
	inline int size(){return v.size();}
	inline void rev(){reverse(v.begin(),v.end());}
	inline void Read(int n){v.resize(n);for(int i=0;i<n;++i)scan(v[i]);}
	inline void Print(int n){if(v.size()<n)v.resize(n);for(int i=0;i<n;++i)putint(v[i],' ');pc('\n');}
	inline poly slice(int x){
		if(x<v.size())return vec(v.begin(),v.begin()+x);
		poly res(v);res.resize(x);
		return res;
	}
};
#define ull unsigned long long
const ull Mod=998244353; 
namespace Basic{
	inline void cpy(int n,poly &f,poly f1){for(int i=0;i<n;++i)f[i]=f1[i];}
	ull f1[N];
	int Wn[N],Log2[N];
	inline void init_poly(int n){
		int cnt1=0;while(n)n>>=1,++cnt1;
		cnt1=(1<<cnt1+1);
		init_inv(cnt1);
		Log2[1]=0;
		for(int i=2;i<=cnt1;++i)Log2[i]=Log2[i>>1]+1;
		int tot=0;
		for(int i=1,base;i<=cnt1;i<<=1){
			base=quick_pow(G,(mod-1)/(i<<1));
			Wn[++tot]=1;for(int j=1;j<i;++j)++tot,Wn[tot]=1ll*Wn[tot-1]*base%mod;
		}
	}
	inline void NTT(poly &f,int len,bool flag){ 
		for(int i=0;i<len;++i)f1[pos[i]]=f[i];
		for(int mid=1,k=2;mid<len;mid<<=1,k<<=1)
			for(int i=0;i<len;i+=k)
				for(int j=0;j<mid;++j){
					ull x=f1[j+i],y=Wn[mid+j]*f1[j+mid+i]%Mod;
					f1[i+j]=x+y,f1[i+j+mid]=Mod+x-y;
				}
		for(int i=0;i<len;++i)f1[i]%=Mod;
		if(!flag){
			reverse(f1+1,f1+len);
			int invn=Inv(len);
			for(int i=0;i<len;++i)f1[i]=1ll*f1[i]*invn%mod;
		}
		for(int i=0;i<len;++i)f[i]=f1[i];
	}
	inline poly Mul(poly a,poly b,int n,int m){
		a.resize(n);b.resize(m);
		int cnt=Log2[n+m-1],len=1<<(cnt+1);
		init_pos(cnt,len);
		NTT(a,len,1);NTT(b,len,1);
		for(int i=0;i<len;++i)a[i]=mul(a[i],b[i]);
		NTT(a,len,0);
		return a.slice(m+n-1);
	}
	inline poly der(poly f,int n){poly ret;ret.resize(n);for(int i=1;i<n;++i)ret[i-1]=mul(f[i],i);return ret;}
	inline poly inter(poly f,int n){poly ret;ret.resize(n);for(int i=1;i<n;++i)ret[i]=mul(f[i-1],Inv(i));return ret;}
	inline poly poly_inv(poly f,int n){
		poly g;g[0]=Inv(f[0]);poly g0,d;
		for(int len=2,cnt=0;(len>>1)<n;len<<=1,++cnt){
			g0=g;init_pos(cnt,len);d=f.slice(len);
			NTT(g0,len,1);NTT(d,len,1);
			for(int i=0;i<len;++i)d[i]=1ll*d[i]*g0[i]%mod;
			NTT(d,len,0);
			fill(d.v.begin(),d.v.begin()+(len>>1),0);
			NTT(d,len,1);
			for(int i=0;i<len;++i)d[i]=1ll*d[i]*g0[i]%mod;
			NTT(d,len,0);
			fill(d.v.begin(),d.v.begin()+(len>>1),0);
			for(int i=0;i<len;++i)g[i]=dec(g[i],d[i]);
		}
		return g.slice(n);
	}
	inline poly div(poly f,poly g,int n,int m){
		poly ret;
		if(n==1){ret[0]=1ll*f[0]*Inv(g[0])%mod;return ret;}
		int cnt=Log2[n],len=1<<(cnt+1),len1=len>>1;
		poly g0=g.slice(len1),q0,f0=f.slice(len1);
		g0=poly_inv(g0,len1);
		init_pos(cnt,len);
		NTT(g0,len,1);NTT(f0,len,1);
		for(int i=0;i<len;++i)q0[i]=1ll*g0[i]*f0[i]%mod;
		NTT(q0,len,0);q0.resize(len1);
		ret=q0;
		NTT(g,len,1);NTT(q0,len,1);
		for(int i=0;i<len;++i)q0[i]=1ll*q0[i]*g[i]%mod;
		NTT(q0,len,0);
		fill(q0.v.begin(),q0.v.begin()+len1,0);
		for(int i=len1;i<len;++i)q0[i]=dec(q0[i],f[i]);
		NTT(q0,len,1);
		for(int i=0;i<len;++i)q0[i]=1ll*q0[i]*g0[i]%mod;
		NTT(q0,len,0);
		for(int i=len1;i<len;++i)ret[i]=dec(ret[i],q0[i]);
		return ret.slice(n);
	}
	inline poly poly_ln(poly f,int n){
		return inter(div(der(f,n),f,n,n),n);
	}
	namespace EXP{
		const int logB=4;
		const int B=16;
		poly f,ret,g[30][B];
		inline void exp(int lim,int l,int r){
			if(r-l<=64){
				for(int i=l;i<r;++i){
					ret[i]=(!i)?1:1ll*ret[i]*inv[i]%mod;
					for(int j=i+1;j<r;++j) Add(ret[j],1ll*ret[i]*f[j-i]%mod);
				}
				return ;
			}
			int k=(r-l)/B;
			poly bl[B];
			for(int i=0;i<B;++i) bl[i].resize(k<<1);
			int len=1<<lim-logB+1;
			for(int i=0;i<B;++i){
				if(i>0){
					init_pos(Log2[len]-1,len);NTT(bl[i],len,0);
					for(int j=0;j<k;++j)
						Add(ret[l+i*k+j],bl[i][j+k]);
				}
				exp(lim-logB,l+i*k,l+(i+1)*k);
				if(i<B-1){
					poly H;H.resize(k<<1);
					for(int j=0;j<k;++j) H[j]=ret[j+l+i*k];
					init_pos(Log2[len]-1,len);;NTT(H,len,1);
					for(int j=i+1;j<B;++j)
						for(int t=0;t<(k<<1);++t) Add(bl[j][t],1ll*H[t]*g[lim][j-i-1][t]%mod); 
				}
			}
		}
		inline void init_exp(){
			for(int i=0;i<f.v.size();++i) f[i]=1ll*f[i]*i%mod;
			int mx=Log2[f.v.size()]+1;
			for(int lim=mx;lim>=logB;lim-=logB){
				int bl=1<<(lim-logB),tot=0,ll=1<<(lim-logB+1);
				init_pos(Log2[ll]-1,ll);
				for(int i=0;i<B-1;++i){
					g[lim][i].resize(bl<<1);
					for(int j=0;j<(bl<<1);++j) g[lim][i][j]=f[j+bl*i];
					NTT(g[lim][i],ll,1);
				}
			}
		}
		//非递归版 
		/*inline poly poly_exp(poly f,int n){
			poly g;g[0]=1;poly g0,h0,dg0,df0,df,g1;
			for(int len=2,len1,cnt=0;(len>>1)<n;len<<=1,++cnt){
				len1=len>>1;
				g0=g;g1=g;dg0=der(g0,len1);df0=der(f.slice(len1),len1);
				df=der(f.slice(len),len);h0=poly_inv(g0,len1);
				init_pos(cnt-1,len1);
				NTT(dg0,len1,1);NTT(h0,len1,1);
				for(int i=0;i<len1;++i)dg0[i]=1ll*dg0[i]*h0[i]%mod;
				NTT(dg0,len1,0);
				for(int i=0;i<len;++i)dg0[i]=dec(dg0[i],df[i]);
				for(int i=0;i<len1-1;++i)dg0[i+len1]=add(dg0[i+len1],dg0[i]),dg0[i]=0;
				NTT(g0,len1,1);
				for(int i=0;i<len1;++i)h0[i]=1ll*g0[i]*h0[i]%mod;
				NTT(h0,len1,0);h0[0]=dec(h0[0],1);
				for(int i=0;i<len1;++i)h0[i+len1]=add(h0[i+len1],h0[i]),h0[i]=0;
				init_pos(cnt,len);
				NTT(h0,len,1);NTT(df0,len,1);
				for(int i=0;i<len;++i)h0[i]=1ll*df0[i]*h0[i]%mod;
				NTT(h0,len,0);h0.resize(len);
				fill(h0.v.begin(),h0.v.begin()+len1,0);
				for(int i=0;i<len;++i)h0[i]=dec(dg0[i],h0[i]);
				h0=inter(h0,len);
				NTT(g1,len,1);NTT(h0,len,1);
				for(int i=0;i<len;++i)g1[i]=1ll*h0[i]*g1[i]%mod;
				NTT(g1,len,0);
				for(int i=len1;i<len;++i)g[i]=dec(g[i],g1[i]);
			}
			return g;
		}*/
	}
	inline poly poly_exp(poly f,int n){
		EXP::f=f;
		EXP::init_exp();
		EXP::exp(Log2[n]+1,0,1<<Log2[n]+1);
		return EXP::ret.slice(n);
	}
	inline poly poly_sqrt(poly f,int n){
		poly g,g0,h,b,a,c;g[0]=Cipolla::cipolla(f[0]);
		h[0]=Inv(g[0]);g0[0]=g[0];g0[1]=g[0];int iv2=Inv(2);
		init_pos(0,1);
		for(int len=2,len1,cnt=0;(len>>1)<n;len<<=1,++cnt){
			len1=len>>1;
			for(int i=0;i<len1;++i)b[i]=1ll*g0[i]*g0[i]%mod;
			NTT(b,len1,0);
			for(int i=0;i<len1;++i)b[i+len1]=dec(b[i],f[i]),b[i]=0;
			for(int i=len1;i<len;++i)b[i]=dec(b[i],f[i]);		
			a=h;a.resize(len1);
			init_pos(cnt,len);
			NTT(a,len,1);NTT(b,len,1);
			for(int i=0;i<len;++i)b[i]=1ll*a[i]*b[i]%mod;
			NTT(b,len,0);
			for(int i=len1;i<len;++i)g[i]=dec(0,1ll*b[i]*iv2%mod);
			if(len>=n)break;
			g0=g;NTT(g0,len,1);
			for(int i=0;i<len;++i)c[i]=1ll*a[i]*g0[i]%mod;
			NTT(c,len,0);
			fill(c.v.begin(),c.v.begin()+len1,0);
			NTT(c,len,1);
			for(int i=0;i<len;++i)c[i]=1ll*a[i]*c[i]%mod;
			NTT(c,len,0);
			for(int i=len1;i<len;++i)h[i]=dec(h[i],c[i]);
		}
		return g.slice(n);
	}
	inline poly poly_pow(poly f,int n,int k){
		int c=0;while(!f[c]&&1ll*c*k<n)++c;poly g;
		if(1ll*c*k>=n){g.resize(n);return g;}
		int iv=Inv(f[c]),b=quick_pow(f[c],k);
		for(int i=c;i<n;++i)f[i]=1ll*iv*f[i]%mod;
		for(int j=c;j<n;++j)g[j-c]=f[j];
		g=poly_ln(g,n);
		for(int i=0;i<n;++i)g[i]=1ll*g[i]*k%mod;
		g=poly_exp(g,n);
		for(int i=c*k,j=0;i<n;++i,++j)f[i]=1ll*g[j]*b%mod;
		fill(f.v.begin(),f.v.begin()+c*k,0);
		return f; 
	}
}
using namespace Basic;
namespace DIVISION{
	inline poly divide(poly F,poly G,int n,int m){
		if(F.v.size()<G.v.size()){G.resize(1);G[0]=0;return G;}
		F.rev();int p=n-m+1;poly INVG=G;INVG.rev();INVG=poly_inv(INVG,INVG.size());
		F=Basic::Mul(F,INVG,p,p).slice(p);
		F.rev();
		return F;
	}
	inline poly module(poly F,poly G,poly Q,int n,int m,int q){
		q=Q.v.size();
		G=Basic::Mul(G,Q,m,q);
		for(int i=0;i<m;++i)Dec(F[i],G[i]);
		return F.slice(m-1);
	}
}
inline poly operator -(poly F,poly G){for(int i=0;i<max(F.size(),G.size());++i)Dec(F[i],G[i]);return F;}
inline poly operator +(poly F,poly G){for(int i=0;i<max(F.size(),G.size());++i)Add(F[i],G[i]);return F;}
inline poly operator *(poly F,poly G){return Basic::Mul(F,G,F.v.size(),G.v.size());}
inline poly operator /(poly F,poly G){return DIVISION::divide(F,G,F.v.size(),G.v.size());}
inline poly operator %(poly F,poly G){
	int n=F.v.size(),m=G.v.size();
	return DIVISION::module(F,G,DIVISION::divide(F,G,n,m),n,m,n-m+1);
}