DS博客作业02--栈和队列

0.PTA得分截图

1.本周学习总结（0-5分）

1.1 栈

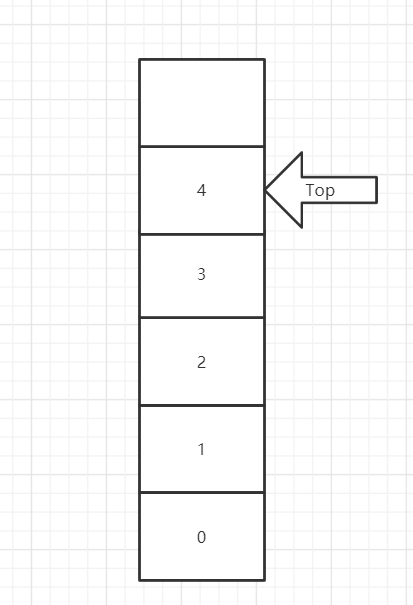
顺序栈的结构

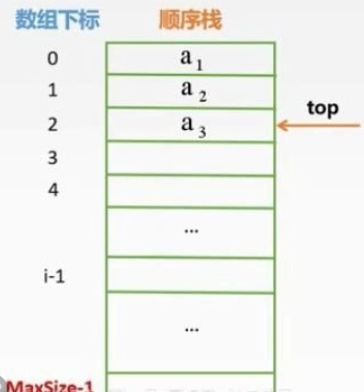
操作函数

定义

typedef struct
{ ElemType data[MaxSize]； //栈中数据元素
int top； //top为栈顶指针
} Stack；
typedef Stack *SqStack;

初始化：

void InitStack(SqStack s)
{
s = new SqStack;//分配一个顺序栈的空间，首地址存放s处
s->top = -1; //栈顶指针置为-1
}

入栈：

bool Push(SqStack &s,ElemType e)
{
if(s->top == MAXSIZE - 1) //判断是否栈满
{
return false;
}
s->data[s->top++] = e; //入栈
return true;
}

出栈：

bool Pop(SqStack &s,ElemType e)
{
if(StackEmpty(s)) //判断是否为空栈
{
return false;
}
e = s->data[s->top--]; //退栈
return true;
}

销毁栈:

void DestroyStack(SqStack s)
{
delete s;
}

链栈的结构

结构：

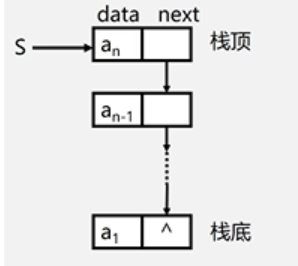
操作函数：

定义：

typedef struct StackNode
{
ElemType data;
struct StackNode next;
}Node,Stack;

初始化：

bool InitStack(Stack &s)
{
s = NULL;
return true;
}

入栈：

void Push(Stack& s, ElemType e)
{
Stack p;
p = new Node;
p->data = e; //新建节点p
p->next = s->next; //插入*p节点作为开始节点
s->next = p;
}

出栈：

bool Pop(Stack& s, ElemType& e)
{
Stack p;
if (StackEmpty(s)) //栈空的情况
return false;
p = s->next; //p指向开始节点，从栈顶开始出栈
e = p->data;
s->next = p->next; //删除p节点
delete p; //释放p节点
return true;
}

1.2 栈的应用

迷宫求解

求迷宫从入口到出口的所有路径是一个经典的程序设计问题。由于计算机解迷宫时，通常用的是“穷举求解”的方法，即从入口出发，顺某一方向向前探索，若能走通，则继续往前走；否则沿原路退回，换一个方向再继续探索，直至所有可能的通路都探索到为止。
为了保证在任何位置都能沿原路退回，显然需要用一个后进先出的结构来保存从入口到当前位置的路径。因此在迷宫求解时应用“栈”是非常适合的。

求解迷宫的算法思想可以描述为：

初始化，将起点加入堆栈；
while(堆栈不为空){
取出栈顶位置为当前位置；
如果 当前位置是终点，
则 使用堆栈记录的路径标记从起点至终点的路径；
否则{
按照从下、右、上、左的顺序将当前位置下一个可以探索的位置入栈；
如果 当前位置的四周均不通
则 当前位置出栈；
}
}

1.3 队列

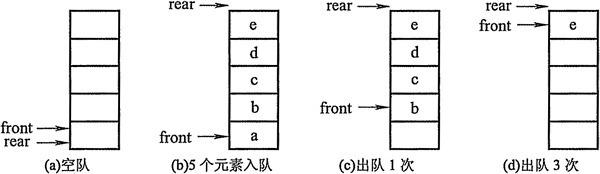
顺序队列的结构、操作函数

结构

typedef struct
{ElemType data[MaxSize] ;//存放队中元素
int front, rear;//队头和队尾指针
}SqQueue;//顺序队类型

初始化

void InitQueue( SqQueue * &.q)
{ q= (SqQueue * )malloc( sizeof(SqQueue));
q-> front=q-> rear=- 1;
}

入队列

bool enQueue(SqQueue * &q, ElemType e)
{ if (q-> rear== MaxSize- 1)//队满上溢出
return false;//返回假
q-> rear++;//队尾增1
q-> data[q-> rear]=e;//rear位置插入元素e
return true;//返回真
}

出队列

bool deQueue(SqQueue * &q, ElemType &e)
{ if (q-> front==q-> rear)//队空下溢出
return false;
q->front++;
e=q -> data[q -> front];
return true;
}

队空和销毁队

void InitQueue(SqQueue * &q)
{
q= (SqQueue * malloc( sizeof(SqQueue));
q-> front=q-> rear=- 1;
}
void DestroyQueue(SqQueue * &q)
{
free(q);
}

环形队列的结构、操作函数

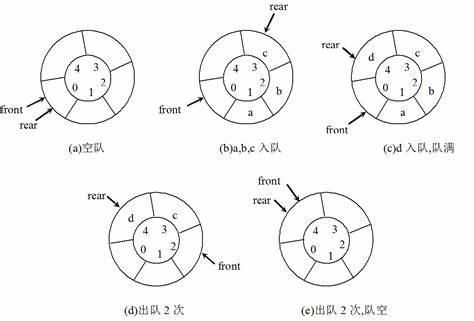
定义：

typedef struct
{
ElemType data[MaxSize];
int front,rear;
} Queue;
typedef Queue *SqQueue;

初始化：

void InitQueue(SqQueue &q)
{ q=new Queue;
q->front=q->rear=0;
}

出队入队：

bool enQueue(SqQueue &q,ElemType e)
{ if ((q->rear+1)%MaxSize==q->front) //队满上溢出
return false;
q->rear=(q->rear+1)%MaxSize;
q->data[q->rear]=e;
return true;
}

bool deQueue(SqQueue * &q, ElemType &e)
{ if (q-> front==q-> rear)//队空下溢出
return false;
q->front=（q->front+1)%MaxSize;
e=q -> data[q -> front];
return true;
}

链队列的结构、操作函数

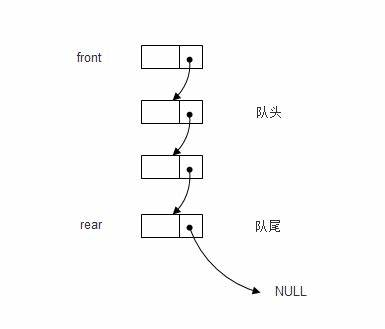
定义：

typedef struct QNode{
QElemType data;
struct Qnode *next;
}Qnode, *QueuePtr;//定义节点类型
typedef struct {
QueuePtr front; //队头指针
QueuePtr rear; //队尾指针
}LinkQueue; //定义队列类型

初始化：

Status InitQueue (LinkQueue &Q)
{
Q.front=Q.rear=new QNode;
if(!Q.front) exit(OVERFLOW);
Q.front->next=NULL;
return OK;
}

入队出队：

Status EnQueue(LinkQueue& Q, QElemType e)
{
p = (QueuePtr)malloc(sizeof(QNode));
if (!p) exit(OVERFLOW);
p->data = e; p->next = NULL;
Q.rear->next = p;
Q.rear = p;
return OK;
}
Status DeQueue(LinkQueue& Q, QElemType& e)
{
if (Q.front == Q.rear) return ERROR;
p = Q.front->next;
e = p->data;
Q.front->next = p->next;
if (Q.rear == p) Q.rear = Q.front;
delete p;
return OK;
}

队列应用：报数问题

.#include<stdio.h>
.#include<malloc.h>
.#define MaxSize 100

typedef int ElemType;

typedef struct
{
ElemType data[MaxSize]; //存放队中元素
int front,rear; //队头和队尾指针
}SqQueue;

//初始化队列
void InitQueue(SqQueue *&q)
{
q=(SqQueue *)malloc(sizeof(SqQueue));
q->front=q->rear=0;
}
//进队
bool enQueue(SqQueue *&q,ElemType e)
{
if((q->rear+1)%MaxSizeq->front)
return false;
q->rear = (q->rear+1)%MaxSize;
q->data[q->rear] = e;
return true;
}
//出队
bool deQueue(SqQueue *&q,ElemType &e)
{
if(q->frontq->rear)
return false;
q->front=(q->front+1)%MaxSize;
e=q->data[q->front];
return true;
}
//判队列是否为空
bool QueueEmpty(SqQueue *q)
{
return (q->frontq->rear);
}
//销毁队列
void DestroyQueue(SqQueue *&q)
{
free(q);
}
//报数
void Bs(int n)
{
int i;
int count=1; //count用来记第几个元素
SqQueue *q;
InitQueue(q);
for(i=1;i<=n;i++)
{
enQueue(q,i);
}
while(!QueueEmpty(q))
{
deQueue(q,i);
if(count%20) //第偶数个元素时，进队
enQueue(q,i);
else
printf("%d ",i); //第奇数个元素时，出队输出
count++;
}
printf("\n");
DestroyQueue(q);
}
int main(void)
{
int n;
printf("输入n的个数：");
scanf("%d",&n);
Bs(n);
return 0;
}

2.PTA实验作业（4分）

此处请放置下面2题代码所在码云地址(markdown插入代码所在的链接)。

2.1 符号配对

2.1.1 解题思路及伪代码

遇到左符号则入栈；
遇到右符号首先考虑栈是否为空：
如果栈为空，则直接输出缺少左符号；
如果栈不为空，则判断右符号是否与栈顶左符号匹配：
如果匹配，就让栈顶的元素出栈；
如果不匹配，就输出缺少右符号；

2.1.2 总结解题所用的知识点

对栈的定义，初始化，入栈，出栈等操作
使用stack库，是速度更快

2.2 银行业务队列简单模拟

2.2.1 解题思路及伪代码

将人数N使用求余运算入队，在队列不为空时，利用flag变量对2进行求余运算
由于A队的业务处理速度是B队的两倍，所以，标志变量每轮递增，A队每轮循环都出队，B队只有当余数为0的时候出队，出队
后重新将标志变量记为0。
循环结束后，判断两队是否均为空，如果不为空，则将剩余队员出列。

2.2.2 总结解题所用的知识点

1.队列的创建，判断是否为空，入队，出队操作
2.使用flag变量来判断空格的输入输出
3.当A或B两个有一个队列为空就退出循环，然后单独输出不为空的队列