快速排序
一、简介
快速排序（Quicksort）由C. A. R. Hoare在1962年提出，是对冒泡排序的一种改进。它采用了一种分治的策略，通常称其为分治法(Divide-and-ConquerMethod)， 快速排序由于排序效率在同为O(N*logN)的几种排序方法中效率较高，因此经常被采用。
二、基本思想
- 先从数列中取出一个数作为基准数。
- 分区过程，将比这个数大的数全放到它的右边，小于或等于它的数全放到它的左边。
- 再对左右区间重复第二步，直到各区间只有一个数。
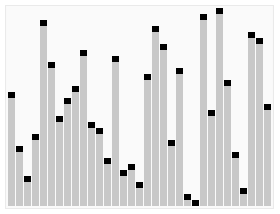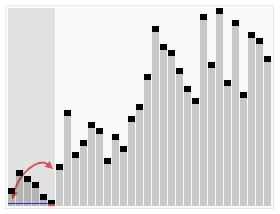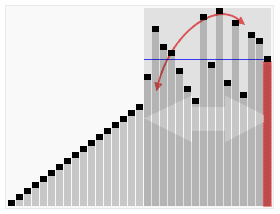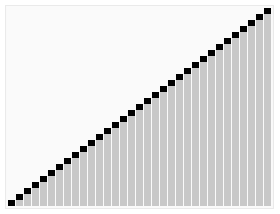
如下图所示：
三、具体实现
1. 实现思路
关于快排的实现的描述，感觉有篇博客[参考2]讲的“挖坑填数+分治法”比较贴切，其描述如下：
以一个数组作为示例，取区间第一个数为枢轴（pivot）。
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
72 |
6 |
57 |
88 |
60 |
42 |
83 |
73 |
48 |
85 |
初始时，i = 0; j = 9; X = a[i] = 72。
从j开始向前找一个比X小或等于X的数。当j=8，符合条件，将a[8]挖出再填到上一个坑a[0]中。a[0]=a[8]; i++;
这样一个坑a[0]就被搞定了，但又形成了一个新坑a[8]，这怎么办了？简单，再找数字来填a[8]这个坑。这次从i开始向后找一个大于X的数，当i=3，符合条件，将a[3]挖出再填到上一个坑中a[8]=a[3]; j—;
数组变为：
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
48 |
6 |
57 |
88 |
60 |
42 |
83 |
73 |
88 |
85 |
i = 3; j = 7; X=72
再重复上面的步骤，先从后向前找，再从前向后找。
从j开始向前找，当j=5，符合条件，将a[5]挖出填到上一个坑中，a[3] = a[5]; i++;
从i开始向后找，当i=5时，由于i==j退出。
此时，i = j = 5，而a[5]刚好又是上次挖的坑，因此将X填入a[5]。
数组变为：
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
48 |
6 |
57 |
42 |
60 |
72 |
83 |
73 |
88 |
85 |
可以看出a[5]前面的数字都小于它，a[5]后面的数字都大于它。因此再对a[0…4]和a[6…9]这二个子区间重复上述步骤就可以了。
2. 代码实现
挖坑填数代码，c++实现：
int AdjustArray(int s[], int l, int r) //返回调整后基准数的位置 { int i = l, j = r; int x = s[l]; //s[l]即s[i]就是第一个坑 while (i < j) { // 从右向左找小于x的数来填s[i] while(i < j && s[j] >= x) j--; if(i < j) { s[i] = s[j]; //将s[j]填到s[i]中，s[j]就形成了一个新的坑 i++; } // 从左向右找大于或等于x的数来填s[j] while(i < j && s[i] < x) i++; if(i < j) { s[j] = s[i]; //将s[i]填到s[j]中，s[i]就形成了一个新的坑 j--; } } //退出时，i等于j。将x填到这个坑中。 s[i] = x; return i; }
快排c++实现：
void quick_sort1(int s[], int l, int r) { if (l < r) { int i = AdjustArray(s, l, r);//先成挖坑填数法调整s[] quick_sort1(s, l, i - 1); // 递归调用 quick_sort1(s, i + 1, r); } }
实际上其他语言的实现就要简洁得多了：
ruby：
def quick_sort(a) (x=a.pop) ? quick_sort(a.select { |i| i <= x }) + [x] + quick_sort(a.select { |i| i > x }) : [] end
erlang：
q_sort([]) -> [];
q_sort([H|R]) -> q_sort([X||X<-R,X<H])++ [H]++ q_sort([X||X<-R,X>=H]).
haskell：
q_sort n=case n of []->[] (x:xs)->q_sort [a|a<-xs,a<=x]++[x]++q_sort [a|a<-xs,a>x]
四、时间复杂度及稳定性
1. 时间复杂度
首先，递归算法的时间复杂度公式：T[n] = aT[n/b] + f(n)。
1) 最优情况下时间复杂度
快速排序最优的情况就是每一次取到的元素都刚好平分整个数组，此时的时间复杂度公式则为：
T[n] = 2T[n/2] + f(n)
T[n/2]为平分后的子数组的时间复杂度，f(n)为平分这个数组时所花的时间
从c++实现代码（AdjustArray）可以知道，f(n)与数组长度成正比，可以用cn来表示（c为常数），
用迭代法：
T[n] = 2T[n/2] + n ----第一次递归 令：n = n/2， = 2{2T[n/4] + (n/2) } + n = 2^2T[n/(2^2)] + 2n ----第二次递归 令：n = n/(2^2)，= 2^2{2T[n/(2^3)] + n/(2^2)} + 2n = 2^3T[n/(2^3)] + 3n ----第三次递归 ...... 令：n = n/(2^(m-1))，=2^mT[1] + mn ----第m次递归(m次后结束) 当最后平分的不能再平分时，也就是说把公式一直往下迭代，到最后得到T[1]时，说明这个公式已经迭代完了（T[1]是常量了）。 得到：T[n/(2^m)] = T[1] ===>> n = 2^m ====>> m = logn； T[n] = 2^mT[1] + mn ；其中m = logn; T[n] = 2^(logn) T[1] + nlogn = n T[1] + nlogn = n + nlogn ；其中n为元素个数 又因为当n >= 2时：nlogn >= n (也就是logn > 1)，nlogn增长最快，所以取后面的nlogn；
综上所述：快速排序最优的情况下时间复杂度为：O(nlogn)。
2) 最差情况下时间复杂度
最差的情况就是每一次取到的元素就是数组中最小/最大的，这种情况其实就是冒泡排序了(每一次都排好一个元素的顺序)这种情况时间复杂度就好计算了，就是冒泡排序的时间复杂度：T[n] = n * (n-1) = n^2 + n;
综上所述：快速排序最差的情况下时间复杂度为：O( n^2 )。
3) 平均时间复杂度
快速排序的平均时间复杂度也是：O(nlogn)。
通常，快排被认为是在所有同数量级(O(nlogn))的排序方法中，其平均性能最好的一个算法。当是如果初始记录序列按关键字有序或者基本有序时，就会退化为冒泡排序，时间复杂度为O(n^2)，为了改进，在取枢轴的时候，通常会用“三者取中”的方法，其实就是取序列头、中间、尾三个元素，然后取其中的中值。
2. 稳定性
从算法思路我们知道，当序列中的元素的值和枢轴相等的时候，是会被交换的，因此，快排不是稳定的排序算法。
五、参考
1. 快速排序算法
3. 快速排序算法
