Longest Palindromic Substring

问题描述

Given a string S, find the longest palindromic substring in S. You may assume that the maximum length of S is 1000, and there exists one unique longest palindromic substring.

 

解决思路

1. 动态规划：时间空间复杂度均为O(n^2)；

2. 中心扩展法：注意考虑奇数长度和偶数长度的情况，时间复杂度为O(n^2)；

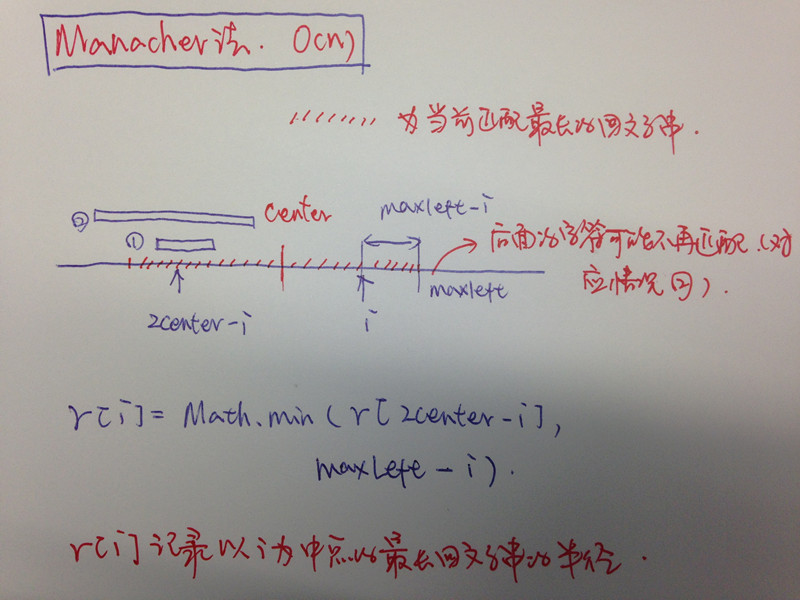
3. Manacher算法：

(1) 用#夹杂在字符串中，进行填充，首字符为$；

(2) 动态规划求解，记录最长回文子串的长度和中心位置；

(3) 去除多余的字符；

时间空间复杂度均为O(n).

 

程序

// dp
public class Solution {
    public String longestPalindrome(String s) {
		if (s == null || s.length() == 0) {
			return "";
		}
		int n = s.length();
		int begin = 0, maxLen = 1;
		boolean[][] isPalindrome = new boolean[n][n];
		// 初始化
		// 单个字符为回文串
		for (int i = 0; i < n; i++) {
			isPalindrome[i][i] = true;
		}
		// 连续两个相同的字符也是回文串
		for (int i = 0; i < n - 1; i++) {
			if (s.charAt(i) == s.charAt(i + 1)) {
				isPalindrome[i][i + 1] = true;
				begin = i;
				maxLen = 2;
			}
		}
		for (int i = n -3; i >= 0; i--) {
			for (int j = i + 2; j < n; j++) {
				if (s.charAt(i) == s.charAt(j) 
					&& isPalindrome[i + 1][j - 1]) {
					isPalindrome[i][j] = true;
					if (j - i + 1 > maxLen) {
						maxLen = j - i + 1;
						begin = i;
					}
				}
			}
		}
		return s.substring(begin, begin + maxLen);
	}
}

　　

public class LongestPalindromicSubstring {
	// 中心匹配法， O(n^2), O(1)
	public String longestPalindrome(String s) {
		if (s == null || s.length() == 0) {
			return "";
		}

		int len = s.length();
		String res = "";

		for (int i = 0; i < len; i++) {
			String s1 = longestPString(s, i, i);
			String s2 = longestPString(s, i, i + 1);
			String longer = s1.length() > s2.length() ? s1 : s2;
			if (longer.length() > res.length()) {
				res = longer;
			}
		}

		return res;
	}

	private String longestPString(String s, int i, int j) {
		int low = 0, high = s.length() - 1;

		while (i >= low && j <= high) {
			if (s.charAt(i) != s.charAt(j)) {
				break;
			}
			--i;
			++j;
		}

		return s.substring(i + 1, j);
	}

	// Manacher算法
	public String longestPalindrome2(String s) {
		if (s == null || s.length() == 0) {
			return "";
		}
		// fill $ and #
		String filled = filledString(s);

		int len = filled.length();
		int[] r = new int[len];
		r[0] = 1;
		int center = 0, maxR = 0;

		for (int i = 1; i < len; i++) {
			int maxLeft = center + maxR;
			if (i < maxLeft) {
				r[i] = Math.min(r[2 * center - i], maxLeft - i);
			} else {
				r[i] = 1;
			}
			// max expand
			while (i - r[i] >= 0 && i + r[i] < len
					&& filled.charAt(i - r[i]) == filled.charAt(i + r[i])) {
				++r[i];
			}
			if (r[i] > maxR) {
				maxR = r[i];
				center = i;
			}
		}

		return removeSign(filled.substring(center - maxR + 1, center + maxR));
	}

	private String removeSign(String s) {
		StringBuilder sb = new StringBuilder();
		for (int i = 0; i < s.length(); i++) {
			char c = s.charAt(i);
			if (c == '#') {
				continue;
			}
			sb.append(c);
		}
		return sb.toString();
	}

	private String filledString(String s) {
		StringBuilder sb = new StringBuilder();
		for (int i = 0; i < s.length(); i++) {
			sb.append("#");
			sb.append(s.charAt(i));
		}
		sb.append("#");
		return "$" + sb.toString();
	}
}

Manacher算法图解