排序算法总结 | 数组
下面对常见的排序算法,包括四种简单排序算法:冒泡排序、选择排序、插入排序和希尔排序;三种平均时间复杂度都是
nlogn的高级排序算法:快速排序、归并排序和堆排序,进行全方面的总结,其中包括代码实现、时间复杂度及空间复杂度分
析和稳定性分析,最后对以上算法进行较大数据量下的排序测试,验证其时间性能。
1. 简单排序算法
1.1 冒泡排序
思想:从后往前,两两比较,将较小的元素交换至前方,一直重复下去,第一遍排序将数组中最小的元素放到了数组的最前
端;同理,第二遍则将数组中第一个元素之后的最小元素交换到第二的位置,以此类推…整个过程可以形象地看作是较小元素
如同“泡泡”一样往上浮,故名冒泡排序( Bubble Sort) .
程序实现
public class BubbleSort {
public void bubbleSort(int[] nums) {
if (nums == null || nums.length == 0) {
return;
}
for (int i = nums.length - 1; i > 0; i--) {
boolean flag = true; // optimize
for (int j = 0; j < i; j++) {
if (nums[j] > nums[j + 1]) {
swap(nums, j, j + 1);
flag = false;
}
}
if (flag) {
break; // if there is no exchange, the array is sorted
}
}
}
private void swap(int[] nums, int j, int i) {
int tmp = nums[j];
nums[j] = nums[i];
nums[i] = tmp;
}
}
时间/空间复杂度分析
最好情况下,数组中的元素为正序,比较次数为n-1 次,交换次数为0次,时间复杂度为O(n);最坏情况下,数组中的元素为逆
序,需要n-1+n-2+…+2+1 = n(n – 1)/2次比较和同样多次数的交换,时间复杂度为O(n^2);平均时间复杂度为O(n^2).
空间复杂度为O(1).
稳定性
基于相邻元素间交换的算法是稳定的。
适用条件
编程实现最为简单,但效率很低,只限于小规模数据。
1.2 选择排序
思想: 每次扫描数组,记录最小元素的下标,扫描完成后将最小元素与第一个元素进行交换,即第一个元素为最小元素,然后
以此类推,直到找完所有剩余元素中的最小元素,交换完成为止。
程序实现
public class SelectSort {
public void selectSort(int[] nums) {
if (nums == null || nums.length == 0) {
return;
}
for (int i = 0; i < nums.length; i++) {
int min = nums[i];
int minIdx = i;
for (int j = i + 1; j < nums.length; j++) {
if (nums[j] < min) {
min = nums[j];
minIdx = j;
}
}
if (minIdx != i) {
swap(nums, i, minIdx);
}
}
}
private void swap(int[] nums, int j, int i) {
int tmp = nums[j];
nums[j] = nums[i];
nums[i] = tmp;
}
}
时间/空间复杂度分析
最好情况需要n*(n – 1)/2次比较, 0次交换,时间复杂度为O(n^2);最坏情况下为n*(n – 1)/2次比较, n次交换,交换次数比冒
泡排序更少(通常交换操作比比较操作更消耗CPU的运行时间),时间复杂度为O(n^2);平均时间复杂度为O(n^2).
空间复杂度为O(1).
稳定性
不稳定,例如对于序列5 8 5 2 9,第一次5和2进行交换,此时5的位置在第二个5的后面,之前的顺序遭到破坏,因而不稳定。
适用条件
小规模数据的排序。
1.3 插入排序
思想: 通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。插入排序在实现上,通常
采用in-place排序(即只需用到O(1)的额外空间的排序),因而在从后向前扫描过程中,需要反复把已排序元素逐步向后挪
位,为最新元素提供插入空间。
程序实现
public class InsertSort {
public void insertSort(int[] nums) {
if (nums == null || nums.length == 0) {
return;
}
for (int i = 1; i < nums.length; i++) {
if (nums[i] < nums[i - 1]) {
int tmp = nums[i];
int j = i;
while (j > 0 && nums[j - 1] > nums[j]) {
nums[j] = nums[j - 1];
--j;
}
nums[j] = tmp;
}
}
}
}
时间/空间复杂度分析
最好情况是元素构成正序,只需要n-1 次比较,不需要挪动元素的位置,时间复杂度为O(n);最坏情况下是元素构成逆序,需
要n-1 次比较和n*(n-1)/2次元素的挪动,时间复杂度为O(n^2);平均时间复杂度为O(n^2).
空间复杂度为O(1).
稳定性
稳定
适用条件
插入排序非常适合小数据量的排序工作,在STL的sort算法和stdlib的qsort算法中,都将插入排序作为快速排序的补充,用于少
量元素的排序(通常为8个或以下)。
1.4 希尔排序
思想: 希尔排序是插入排序的一种高速的改进版本,基本思想是先取一个小于n的整数d1 作为第一个增量,把文件的全部记录分成d1 个组。所有距离为dl的倍数的记录放在同一个组中。先在各组内进行直接插人排序;然后,取第二个增量d2<d1重复上述的分组和排序,直至所取的增量dt=1(dt< dt-l<…<d2<d1),即所有记录放在同一组中进行直接插入排序为止。
程序实现
public class ShellSort {
public void shellSort(int[] nums) {
if (nums == null || nums.length == 0) {
return;
}
for (int gap = nums.length / 2; gap > 0; gap /= 2) {
for (int i = gap; i < nums.length; i += gap) {
int tmp = nums[i];
if (nums[i] < nums[i - gap]) {
int j = i;
while (j - gap >= 0 && nums[j - gap] > nums[j]) {
nums[j] = nums[j - gap];
j -= gap;
}
nums[j] = tmp;
}
}
}
}
}
时间/空间复杂度分析
时间复杂度为O(nlogn^2),大约为O(n^1.3),比起前三种简单排序算法快得多。
空间复杂度为O(1).
稳定性
不稳定,单趟的插入排序是稳定的,但是不同组的插入排序有可能打乱原有的元素顺序。
适用条件
虽然比不上时间复杂度为O(n*logn)的高级排序算法快,但在中等规模的数据集上仍然表现不错,并且编程较简单。甚至有些专家们提倡,几乎任何排序工作在开始时都可以用希尔排序,若在实际使用中证明它不够快, 再改成快速排序这样更高级的排序算法.
2 高级排序算法
2.1 快速排序算法
思想: 快速排序是冒泡排序的一种改进,交换顺序不再限于相邻元素间。基本思想为通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。
实现
有递归和非递归两种实现方式,其中partition函数是共用的。值得说明的是,后续的测试表明, 递归版本的快排在运行时间上要优于非递归版本。
public class QuickSort {
// recursion
public void quickSortRec(int[] nums) {
if (nums == null || nums.length == 0) {
return;
}
recHelper(nums, 0, nums.length - 1);
}
private void recHelper(int[] nums, int begin, int end) {
if (begin >= end) {
return;
}
int mid = partition(nums, begin, end);
recHelper(nums, begin, mid - 1);
recHelper(nums, mid + 1, end);
}
private int partition(int[] nums, int low, int high) {
int begin = low - 1, end = high;
int pivot = nums[end];
while (true) {
while (begin < end && nums[++begin] <= pivot) {
;
}
while (begin < end && nums[--end] >= pivot) {
;
}
if (begin >= end) {
break;
}
swap(nums, begin, end);
}
swap(nums, begin, high);
return begin;
}
private void swap(int[] nums, int begin, int end) {
int tmp = nums[begin];
nums[begin] = nums[end];
nums[end] = tmp;
}
// no recursion
public void quickSortNoRec(int[] nums) {
if (nums == null || nums.length == 0) {
return;
}
Stack<Integer> s = new Stack<Integer>();
s.push(0);
s.push(nums.length - 1);
while (!s.isEmpty()) {
int high = s.pop();
int low = s.pop();
int mid = partition(nums, low, high);
if (mid > low) {
s.push(low);
s.push(mid - 1);
}
if (mid < high) {
s.push(mid + 1);
s.push(high);
}
}
}
}
时间/空间复杂度分析
最好情况是,每执行一次分割,都能将数组分为两个长度近乎相等的片段,然后这样递归下去,递推式为T(n) = 2*T(n/2) + O(n),其中O(n)为一次partition的时间消耗,因此最好和平均时间复杂度均为O(nlogn);最坏情况下,数组元素为逆序,此时的递推式退化为T(n) = T(n – 1) + O(n),时间复杂度为O(n^2).
空间复杂度上,尽管快排是in-place的,但递归需要一定的空间消耗,最好情况下, logn级别次数的递归调用,将消耗O(logn)的空间;最坏情况下,则是n级别次数的递归调用,此时的空间复杂度为O(n).
稳定性
不稳定,中枢元素与对应元素交换时将可能打乱数组的原本顺序。
适用条件
平均上看,快排的时间性能最好,适用于中大规模的数据排序。有许多种方法可以尽量避免快排的最坏情况,如每次随机选择枢纽元素,或者一开始选择首中尾中的中值元素作为枢纽元素等。
2.2 归并排序算法
思想: 是建立在归并操作上的一种有效的排序算法,是采用分治法( Divide and Conquer)的一个非常典型的应用。每个递归过程涉及三个步骤 :
第一, 分解: 把待排序的 n 个元素的序列分解成两个子序列, 每个子序列包括 n/2 个元素.
第二, 治理: 对每个子序列分别调用归并排序MergeSort, 进行递归操作
第三, 合并: 合并两个排好序的子序列,生成排序结果.
实现
public class MergeSort {
private int[] copy;
// recursion
public void mergeSortRec(int[] nums) {
if (nums == null || nums.length == 0) {
return;
}
copy = new int[nums.length];
mergeSortRecHelper(nums, 0, nums.length - 1);
}
private void mergeSortRecHelper(int[] nums, int begin, int end) {
if (begin >= end) {
return;
}
int mid = begin + (end - begin) / 2;
mergeSortRecHelper(nums, begin, mid);
mergeSortRecHelper(nums, mid + 1, end);
mergeArrays(nums, begin, mid, end);
}
private void mergeArrays(int[] nums, int begin, int mid, int end) {
int low = begin, high = mid + 1;
int k = begin;
while (low <= mid && high <= end) {
if (nums[low] < nums[high]) {
copy[k++] = nums[low++];
} else {
copy[k++] = nums[high++];
}
}
while (low <= mid) {
copy[k++] = nums[low++];
}
while (high <= end) {
copy[k++] = nums[high++];
}
// copy to origin array
for (int i = begin; i <= end; i++) {
nums[i] = copy[i];
}
}
// no recursion
public void mergeSortNoRec(int[] nums) {
if (nums == null || nums.length == 0) {
return;
}
copy = new int[nums.length];
int step = 2;
while (true) {
int start = 0;
while (start < nums.length) {
int end = start + step - 1;
if (end > nums.length - 1) {
end = nums.length - 1;
}
int mid = start + (end - start) / 2;
mergeArrays(nums, start, mid, end);
start = end + 1;
}
// important statement
if (step > nums.length) {
break;
}
step *= 2;
}
}
}
时间/空间复杂度分析
各种情况下的时间复杂度均为O(nlogn)
空间复杂度为O(n)
稳定性
稳定
适用条件
中等规模的数据量,大规模的数据将受到内存限制(空间复杂度)。
2.3 堆排序算法
思想:首先需要清楚二叉堆的定义,二叉堆是完全二叉树或者是近似完全二叉树,堆的存储一般都用数组实现。
二叉堆满足以下2个特性:
1 .父结点的键值总是大于或等于(小于或等于)任何一个子节点的键值。
2.每个结点的左子树和右子树都是一个二叉堆(都是最大堆或最小堆)。
当父结点的键值总是大于或等于任何一个子节点的键值时为最大堆。当父结点的键值总是小于或等于任何一个子节点的键值时为最小堆。
堆排序的思想是,先对整个数组堆化处理,形成最大堆(最终形成升序的序列),此时位于数组首位的元素为最大,将其换至末尾,此时调整整个堆(即所有除了末尾以外的元素),调整完后首尾元素又是当前的最大元素,将其换至倒数第二个位置,以此类推,直到整个序列有序(升序)为止。
实现
public class HeapSort {
public void heapSort(int[] nums) {
if (nums == null || nums.length == 0) {
return;
}
// build the max-heap of array
buildMaxHeap(nums, nums.length);
heapSortHelper(nums);
}
private void heapSortHelper(int[] nums) {
for (int i = nums.length - 1; i > 0; i--) {
swap(nums, 0, i);
fixMaxHeap(nums, 0, i);
}
}
private void swap(int[] nums, int i, int j) {
int tmp = nums[i];
nums[i] = nums[j];
nums[j] = tmp;
}
private void buildMaxHeap(int[] nums, int n) {
for (int i = n / 2 - 1; i >= 0; i--) {
fixMaxHeap(nums, i, n);
}
}
private void fixMaxHeap(int[] nums, int i, int n) {
int tmp = nums[i];
int j = 2 * i + 1;
while (j < n) {
if (j + 1 < n && nums[j + 1] > nums[j]) {
// choose the max between left and right
j++;
}
if (nums[j] <= tmp) {
break;
}
nums[i] = nums[j];
i = j;
j = 2 * j + 1;
}
nums[j] = tmp;
}
}
时间/空间复杂度分析
建堆的时间复杂度为O(n),调整一次堆的时间为O(logn),排序过程中对n-1 个元素进行了调整操作,最终的时间复杂度依然为O(nlogn).
空间复杂度为O(1).
[建堆时间复杂度O(n): http://blog.sina.com.cn/s/blog_691a84f301014aze.html]
稳定性
堆排序是不稳定的:
比如: 3 27 36 27,
如果堆顶3先输出,则,第三层的27(最后一个27)跑到堆顶,然后堆稳定,继续输出堆顶,是刚才那个27,这样说明后面的
27先于第二个位置的27输出,不稳定。
适用条件
大规模数据量
3. 各个排序算法的比较测试
结论:
(1) 简单排序中,希尔排序的时间性能最好,插入排序次之,冒泡排序性能最差;
(2) 三种高级排序的时间性能:快速排序 > 归并排序 > 堆排序,递归版本的快排性能较非递归要好,而对于归并排序而言,非递归版本性能较好。
4. 排序算法总结图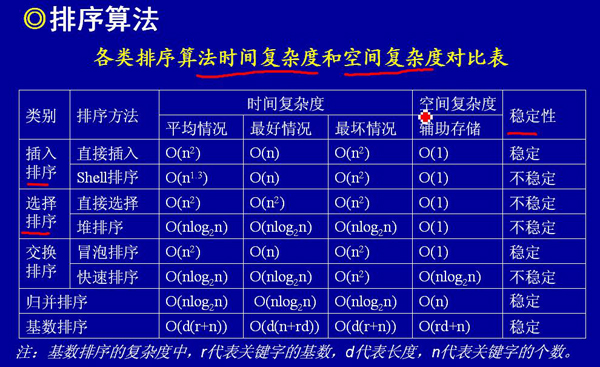
(图片来源: http://www.cnblogs.com/biyeymyhjob/archive/2012/07/17/2591457.html)
参考资料
1. 排序算法汇总总结: http://www.cnblogs.com/biyeymyhjob/archive/2012/07/17/2591457.html
2. 白话经典排序算法系列: http://blog.csdn.net/morewindows/article/details/6709644/




