本篇主要介绍排序算法中的快速排序 堆排序和归并排序
一 快速排序
1 快排思路：
- 取一个元素p(第一个元素)，是元素p归位（去它该去的地方）
- 列表被p分成两部分，左边的都比p小，右边的都比p大
- 递归完成排序
2 快速排序的问题：
- 最坏情况
- 递归
3 图示说明
4 如何实现归并
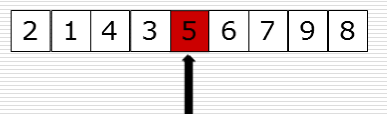
先把5取出来，这时候就会有一个空位，从右边找比5小的数填充过来，现在右边有一个空位了，从左边找比5大的放到右边的空位上。依次类推，只要left和right碰在一起，这样就找到5的位置了
如图示：
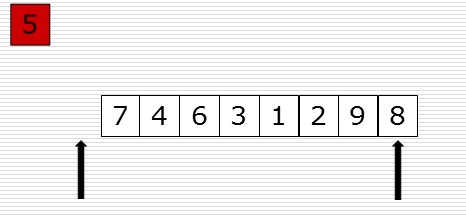
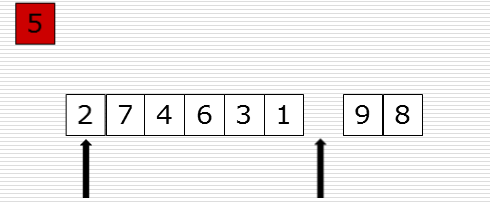
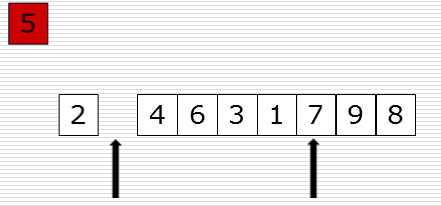
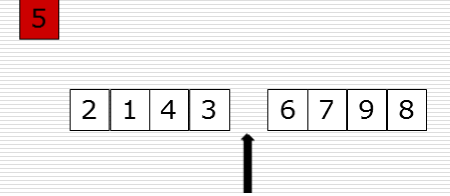
这样在把找到的5的位置放进去去ok了
实现代码：
def partition(li, left, right): ''' 归位 :param li: :param left: :param right: :return: ''' tmp = li[left] while left < right: while left < right and li[right] >= tmp: # 从右面寻找比tmp小的数 right -= 1 # 指针往左走一步 li[left] = li[right] # 在right找到比tmp小的数，将这个数从right放到left while left < right and li[left] <= tmp: left += 1 li[right] = li[left] # 把左边的值写到右边的空位 li[left] = tmp # 把tmp位 return left li = [5, 7, 4, 6, 3, 1, 2, 9, 8] print(li) partition(li, 0, len(li) - 1) print(li) ''' [5, 7, 4, 6, 3, 1, 2, 9, 8] [2, 7, 4, 6, 3, 1, 2, 9, 8] [2, 7, 4, 6, 3, 1, 7, 9, 8] [2, 1, 4, 6, 3, 1, 7, 9, 8] [2, 1, 4, 6, 3, 6, 7, 9, 8] [2, 1, 4, 3, 3, 6, 7, 9, 8] [2, 1, 4, 3, 3, 6, 7, 9, 8] [2, 1, 4, 3, 5, 6, 7, 9, 8] ''' def quick_sort(li, left, right): if left < right: # 至少两个元素 mid = partition(li, left, right) quick_sort(li, left, mid - 1) quick_sort(li, mid + 1, right) quick_sort(li, 0, len(li) - 1) print(li)
二 堆排序
1 堆排序涉及到的概念
什么是堆：
- 堆是一种特殊的完全二叉树结构
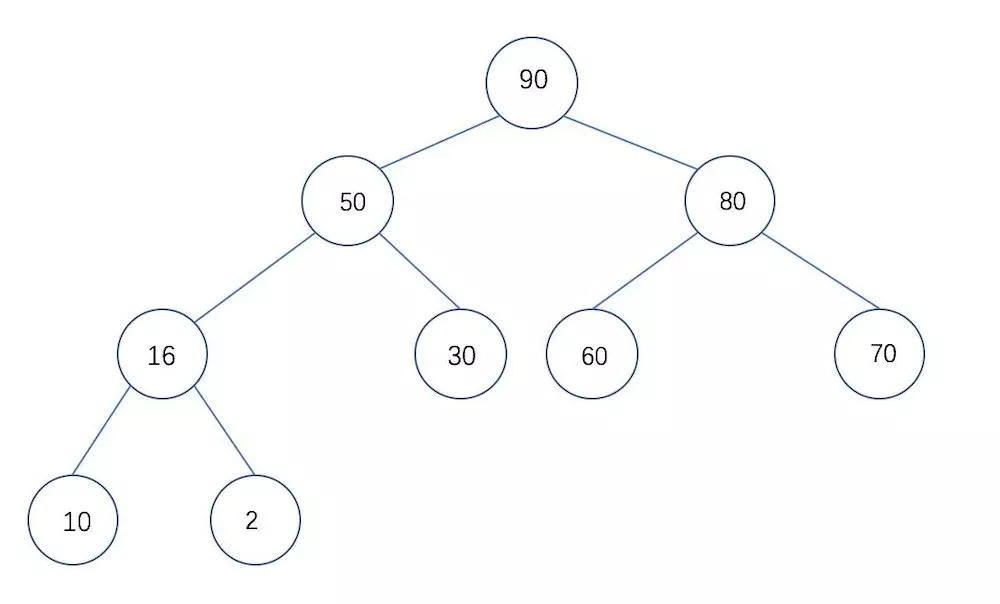
- 大根堆：一颗完全二叉树, 满足任一节点都比其他孩子节点大
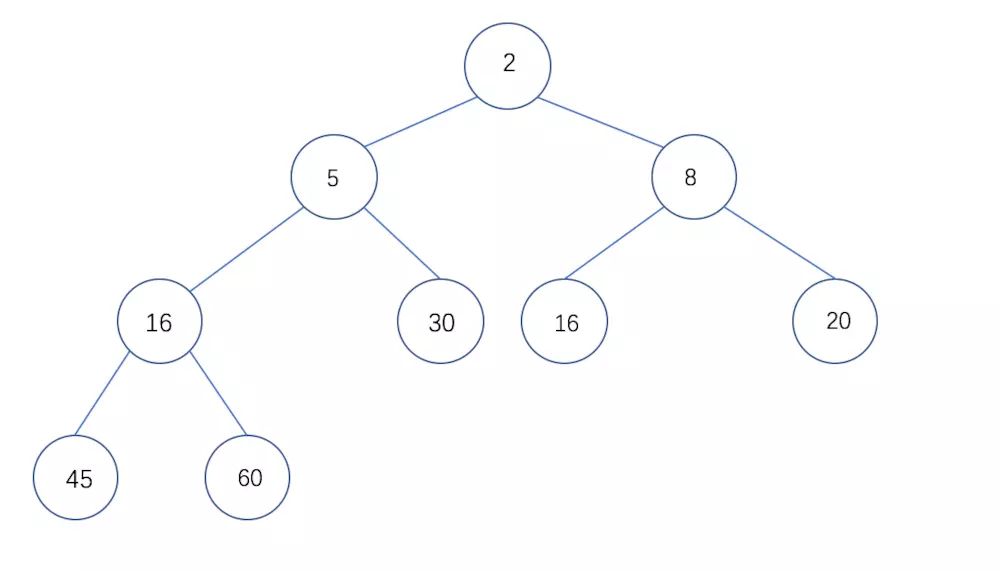
- 小根堆：一颗完全二叉树, 满足任一节点都比其孩子节点小
大根堆：
小根堆：
什么是二叉树：
- 度不超过2的树
- 每个节点最多有两个孩子节点
- 两个孩子节点被区分为左孩子节点和右孩子节点
- 满二叉树：一个二叉树如果每一个层的节点数达到最大值,则这个二叉树就是满二叉树
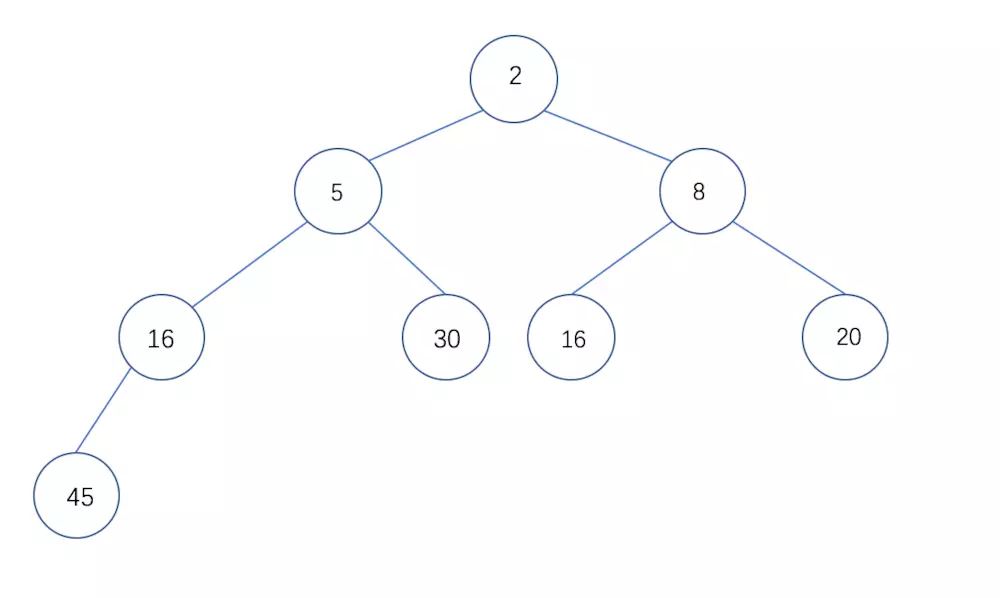
- 完全二叉树：叶节点只能出现在最下层和次下层，并且最下面一层的节点都集中在该层最左边的若干位置的二叉树
完全二叉树：
2 堆排序的实现过程
-
建立堆
-
得到堆顶元素，为最大元素
-
去掉堆顶，将堆最后一个元素放到堆顶，此时可通过一次调整重新使堆有序。
-
堆顶元素为第二大元素
-
重复第三个步骤，直到堆变空
首先把2和9的位置互换：
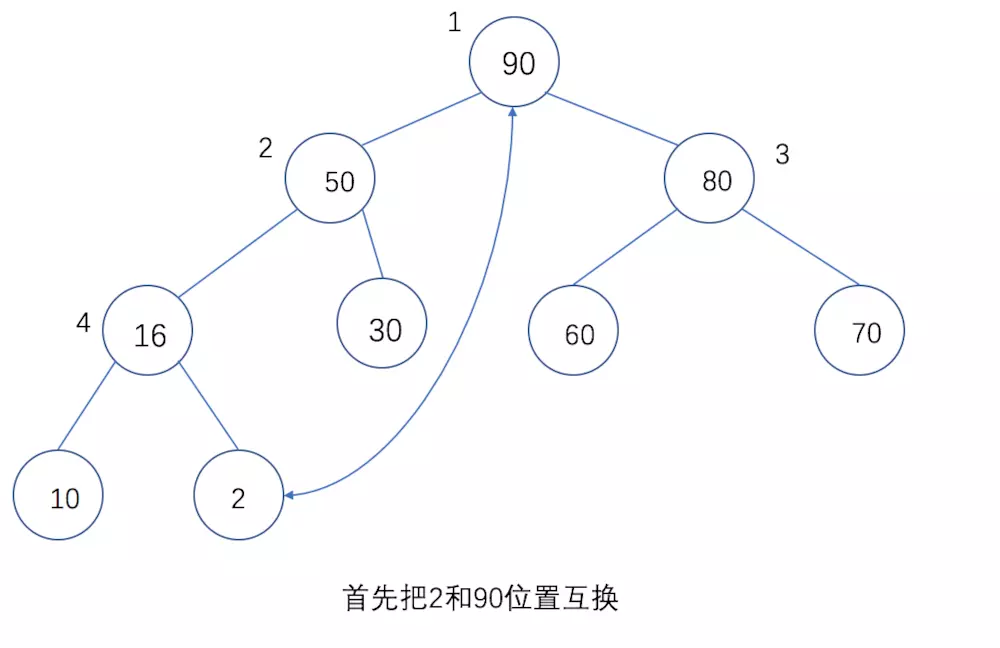
互换位置后把2的位置进行调整，重新构造出一个大根堆：
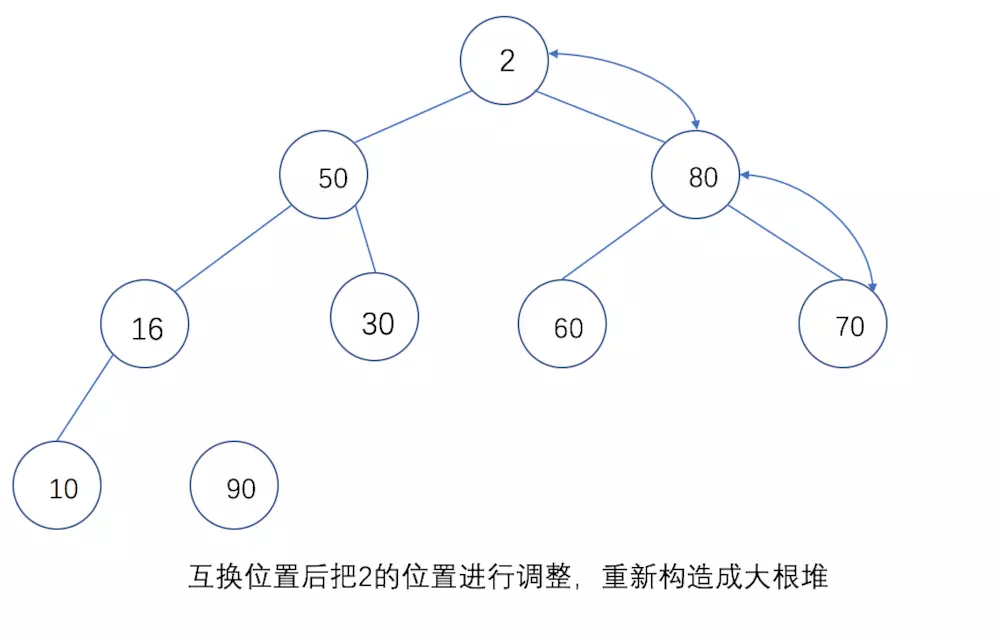
然后再把10和80的位置互换，继续进行上面的步骤：
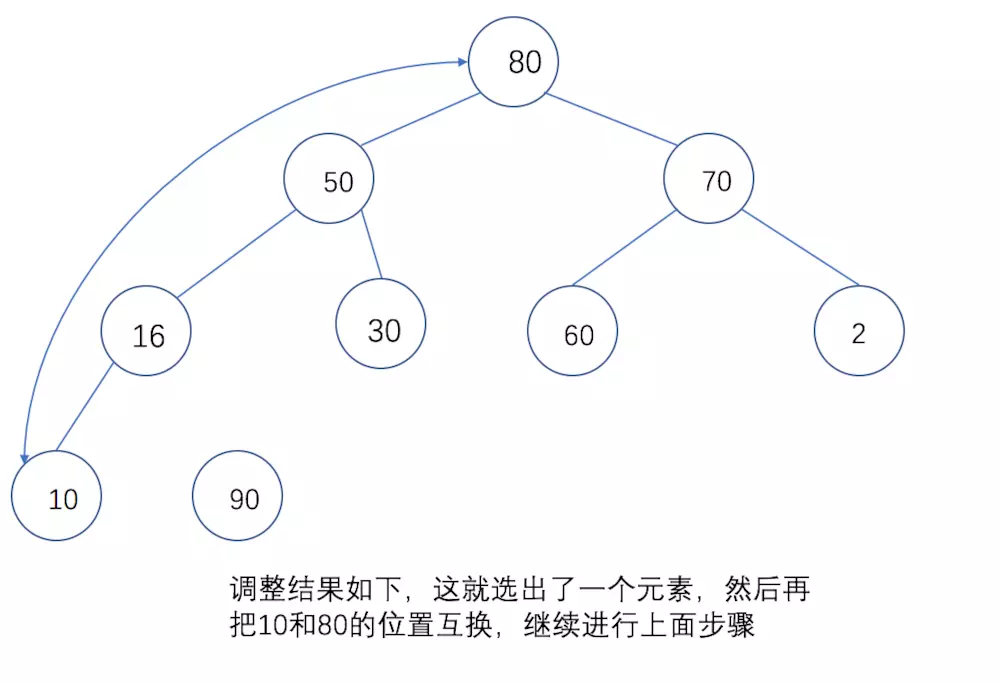
3 堆排序实现代码
def sift(li, low, high): """ 调整成大顶堆，初始堆时，从下往上；交换堆顶与堆尾后，从上往下调整 :param li: 列表 :param low: 堆的根节点位置 :param high: 堆的最后一个元素的位置 :return: """ # 当列表第一个是以下标0开始，结点下标为i,左孩子则为2*i+1,右孩子下标则为2*i+2; # 若下标以1开始，左孩子则为2*i,右孩子则为2*i+１ i = low # i最开始指向根节点 j = 2 * i + 1 # j开始是左节点孩子 tmp = li[low] # 把堆顶存起来 while j <= high: # 只要j位置有数 if j + 1 <= high and li[j + 1] > li[j]: # 如果这个节点右孩子存在并且比左孩子大，将j指向右孩子节点 j = j + 1 # if li[j] > tmp: li[i] = li[j] i = j # 往下看一层 j = 2 * i + 1 else: # tmp更大， 把tmp放到i的位置上 break li[i] = tmp # 把tmp放到某一级领导位置上 def heap_sort(li): n = len(li) # 1 建堆 for i in range((n - 2) // 2, -1, -1): # i表示建堆的时候调整的部分的根的下标 sift(li, i, n - 1) # 2 挨个出数 for j in range(n - 1, -1, -1): # j表示堆最后一个元素的位置 # i指向当前堆的最后一个元素 li[0], li[j] = li[j], li[0] sift(li, 0, j - 1) # i-1是新的high（最后一个的位置）
代码讲解：
- 第一个循环做的事情是把序列调整为一个大根堆(sift函数）
- 第二个循环是把堆顶元素和堆末尾的元素交换，然后把剩下的元素调整为一个大根堆(sift函数)
我们要排序的序列为[50, 16, 30, 10, 60, 90, 2, 80, 70]，而我们所谓的调整大根堆，其实就是按照从右往左，从下到上的顺序，把每颗小树调整为一个大根堆
4 堆排序的时间复杂度
在正式排序时，n个结点的完全二叉树的深度为⌊log2n⌋+1，并且有n个数据则需要取n-1次调整成大顶堆的操作，每次调整成大顶堆的时间复杂度为O(log2n)。因此，重建堆的时间复杂度可近似看做: O(nlogn)。
5 堆排序python内置模块
import heapq import random li = list(range(100)) random.shuffle(li) heapq.heapify(li) # 建立堆 heapq.heappop(li) # 为此弹出一个最小数 n = len(li) for i in range(n): print(heapq.heappop(li))
6 堆排序— topk问题
现在又n个数，设计算法得到前K大的数。 (k<n)
解决思路：
- 第一种：排序号切片 O(nlogn)
- 第二种：使用冒泡排序 O(k)
- 第三种：堆排序思路 O(nlogk)
堆排序实现思路：
- 取列表前k个元素建立一个小根堆。对顶就是目前第K大的数
- 依次向后遍历原列表,对于列表中的元素,如果小于堆顶则忽略该元素;如果大于堆顶，则将堆顶更换为该元素并且对堆进行一次调整
- 遍历列表所有元素后, 倒序弹出堆顶
三 归并排序
1 什么是归并排序
假设现在的列表分两段有序,如何将其合成为一个有序列表 [2,5,7,8,9|1,3,4,6]
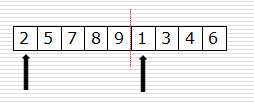
一次归并代码
def merge(li, low, mid, high): i = low j = mid + 1 ltmp = [] while i <= mid and j <= high: # 只要左右两边都有数 if li[i] < li[j]: ltmp.append(li[i]) i += 1 else: ltmp.append(li[j]) j += 1 # while执行完肯定有一部分没数了 while i <= mid: ltmp.append(li[i]) i += 1 while j <= high: ltmp.append(li[j]) j += 1 li[low:high + 1] = ltmp
2 归并排序的实现
分解：将列表约分越小,直到分成一个元素
终止条件： 一个元素是有序的
合并： 将两个有序列表归并，列表越来越大
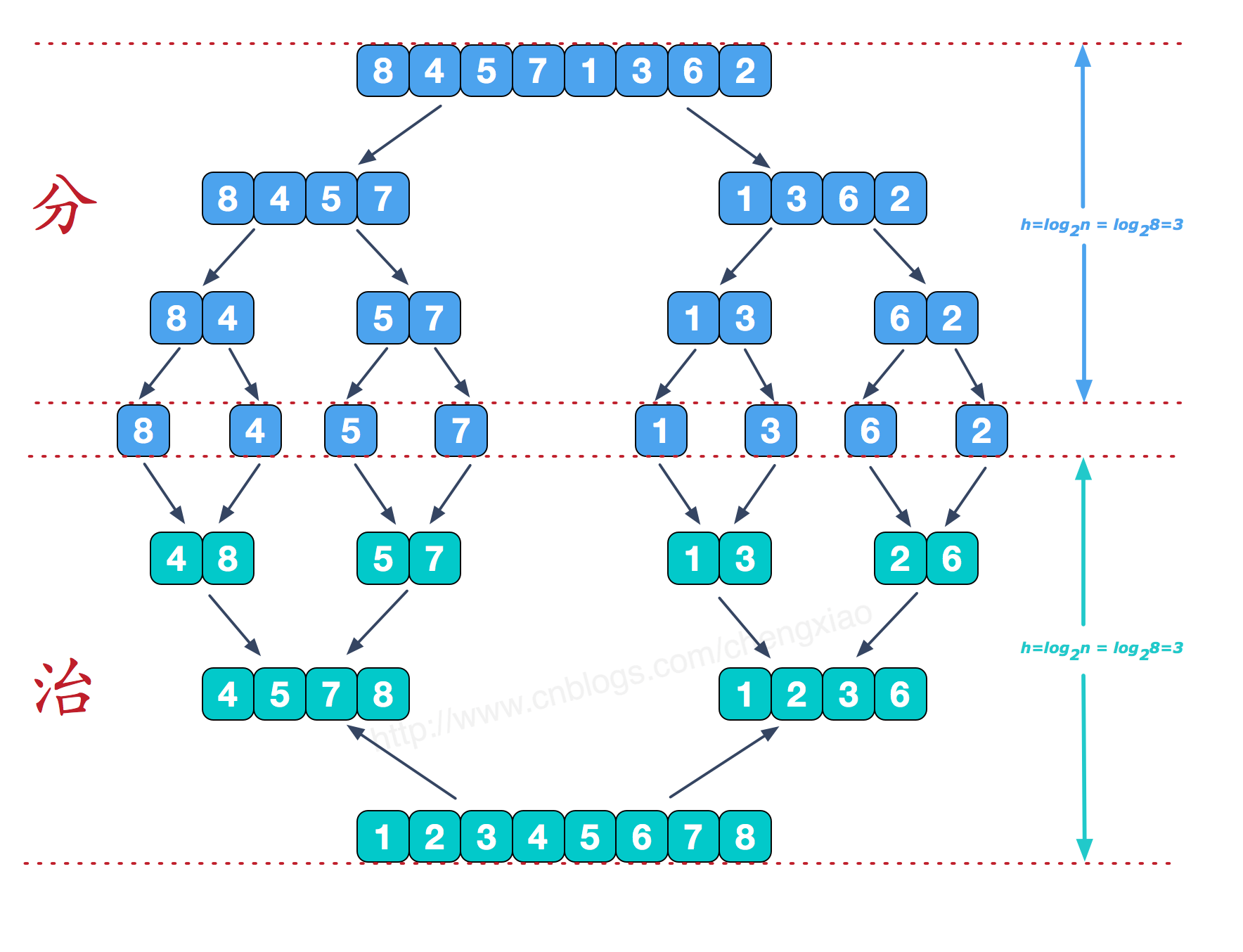
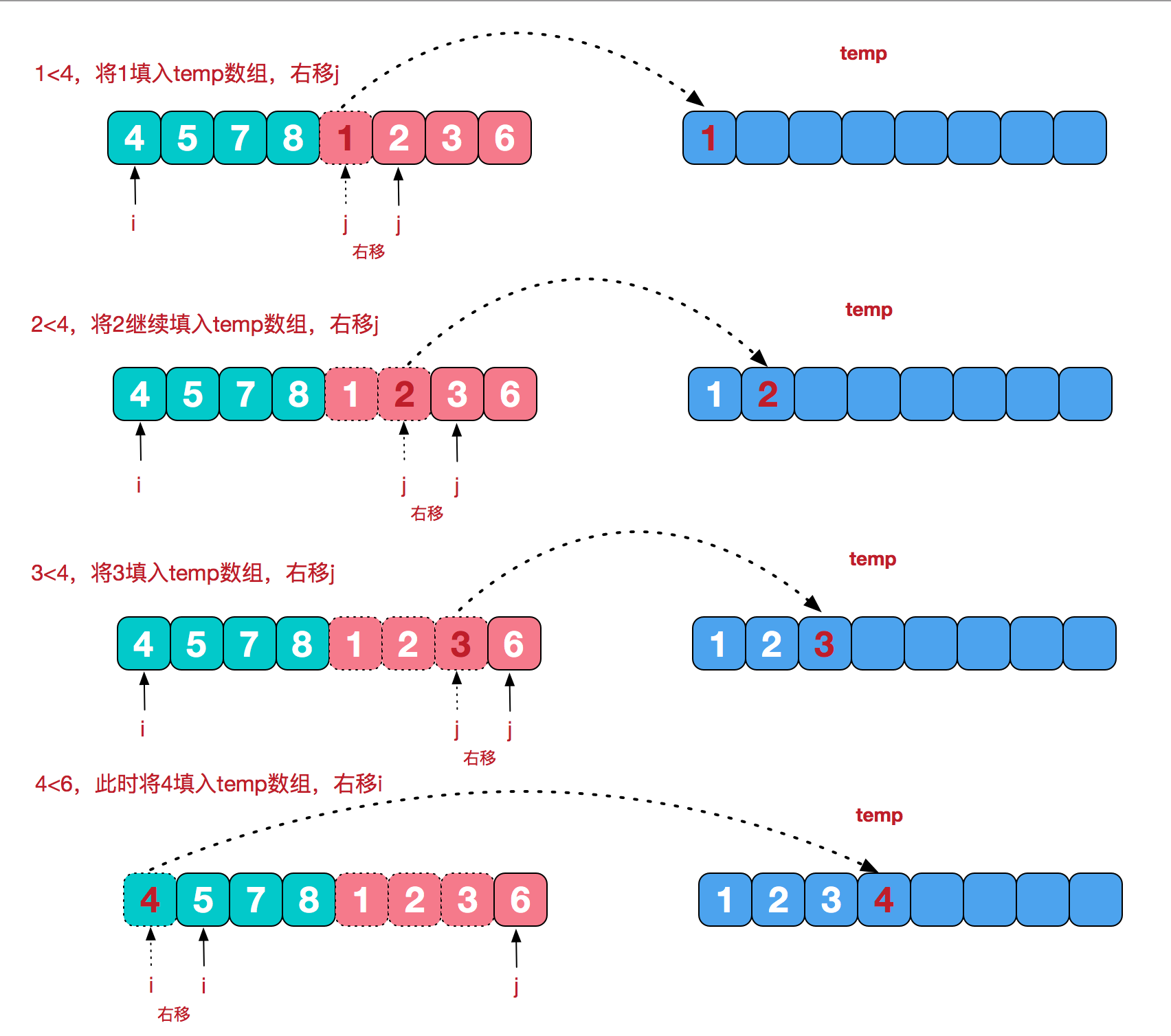
实现代码：
def merge(li, low, mid, high): i = low j = mid + 1 ltmp = [] while i <= mid and j <= high: # 只要左右两边都有数 if li[i] < li[j]: ltmp.append(li[i]) i += 1 else: ltmp.append(li[j]) j += 1 # while执行完肯定有一部分没数了 while i <= mid: ltmp.append(li[i]) i += 1 while j <= high: ltmp.append(li[j]) j += 1 li[low:high + 1] = ltmp def merge_sort(li, low, high): if low < high: # 至少有两个元素，递归 mid = (low + high) // 2 merge_sort(li, low, mid) merge_sort(li, mid + 1, high) merge(li, low, mid, high)
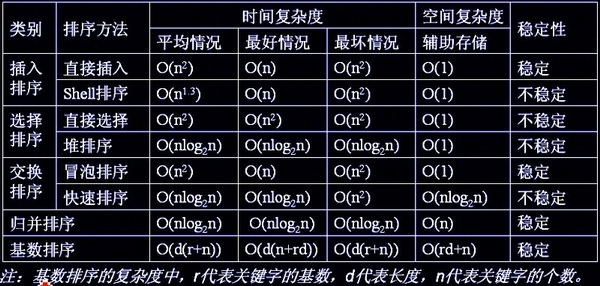
四 NB三人组总结
(1) 三种排序算法的时间复杂度都是O(nlogn)
(2) 一般情况下,就运行时间而言： 快速排序<归并排序<堆排序
(3) 三种排序算法的缺点：
- 快速排序：极端情况下排序效率低
- 归并排序：需要额外的内存开销
- 堆排序： 在快的排序算法中相对较慢
五 其他排序算法
1 希尔排序
希尔排序是一种插入排序算法 过程如下：
- 首先取一个整数d1=n/2，将元素分为d1个组，每组相邻量元素之间距离为d1，在各组内进行直接插入排序
- 取第二个整数d2=d1/2，重复上述分组排序过程，直到di=1，即所有元素在同一组内进行直接插入排序。
- 希尔排序每趟并不使某些元素有序，而是使整体数据越来越接近有序；最后一趟排序使得所有数据有序。
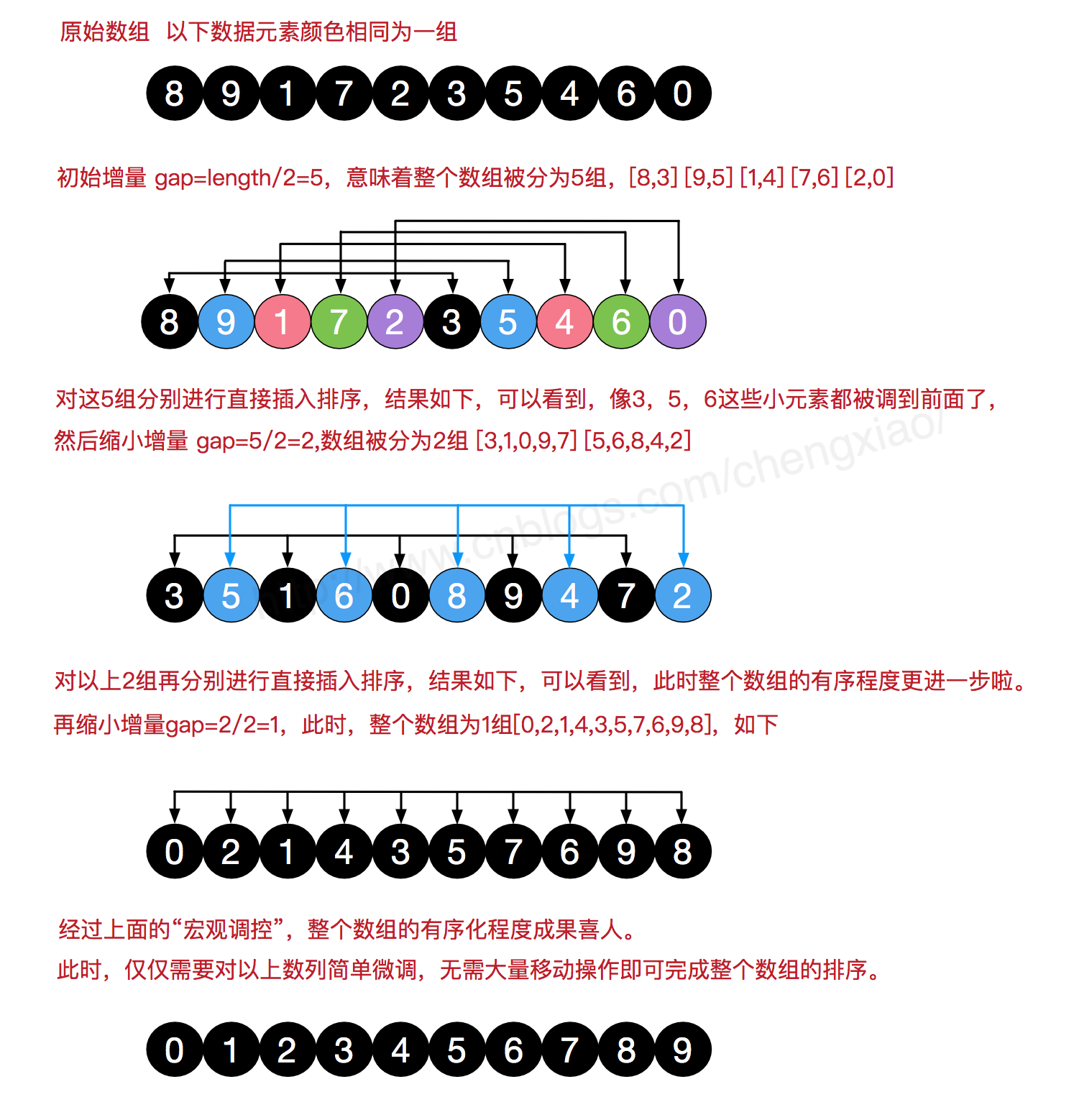
实现代码：
def insert_sort_gap(li, gap): for i in range(gap, len(li)): tmp = li[i] j = i - gap while j >= 0 and li[j] > tmp: li[j + gap] = li[j] j -= gap li[j + gap] = tmp def shell_sort(li): d = len(li) // 2 # 长度除以2 while d >= 1: insert_sort_gap(li, d) d //= 2
2 计数排序
对列表进行排序, 已知列表的范围都在0到100之间，设计时间复杂度为O(n)的算法
def count_sort(li, max_count=100): count = [0 for _ in range(max_count + 1)] for val in li: count[val] += 1 li.clear() for index, val in enumerate(count): for i in range(val): li.append(index)
3 桶排序
在计数排序中列表范围只能再0到100之间，如果元素的范围⽐较⼤（⽐如在1到1亿之间）计数算法则无法实现，
桶排序(Bucket Sort)：⾸先将元素分在不同的桶中，在对每个桶中的元素排序
实现代码：
def bucket_sort(li, n=100, max_num=10000): buckets = [[] for _ in range(n)] # 创建n个桶 for var in li: i = min(var // (max_num // n), n - 1) # i 表示var放到几号桶里 buckets[i].append(var) # 把var加到桶里边 # 保持桶内的顺序 for j in range(len(buckets[i]) - 1, 0, - 1): if buckets[i][j] < buckets[i][j - 1]: buckets[i][j], buckets[i][j - 1] = buckets[i][j - 1], buckets[i][j] else: break sorted_li = [] for buc in buckets: sorted_li.extend(buc) return sorted_li
4 基数排序
多关键字排序：假如现在有一个员工表，要求按照薪资排序，年龄相同的员工按照年龄排序。
- 先按照年龄进行排序, 在安装薪资简写稳定排序
- 对 32,13,94,52,17,54,93排序,是否可以看做多关键字排序?
基数排序效率：
- 时间复杂度： O(kn)
- 空间复杂度： O(k+n)
- K表示数字位数
def radix_sort(li): max_num = max(li) # 最大值 例如： 99->2, 888->3, 10000->5 it = 0 while 10 ** it <= max_num: buckets = [[] for _ in range(10)] for val in li: # 取位数 列：987 it=1 987//10-98 98%10->8; it=2 987//100->9 9%10=9 digit = (val // 10 ** it) % 10 buckets[digit].append(val) li.clear() # 把数重新写回li for buc in buckets: li.extend(buc) it += 1 import random li = list(range(10000)) random.shuffle(li) radix_sort(li) print(li)
