一 树
1 什么是树
每个节点有零个或多个子节点;没有父节点的节点称为根节点;每一个非根节点有且只有一个父节点;除了根节点外,每个子节点可以分为多个不相交的子树;
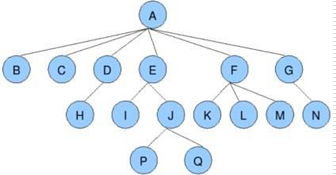
树(tree)是包含n(n>0)个结点的有穷集,其中:
(1)每个元素称为结点(node);
(2)有一个特定的结点被称为根结点或树根(root)。
(3)除根结点之外的其余数据元素被分为m(m≥0)个互不相交的集合T1,T2,……Tm-1,其中每一个集合Ti(1<=i<=m)本身也是一棵树,被称作原树的子树(subtree)。
2 相关术语
- 节点的度:一个节点含有的子树的个数称为该节点的度;
- 叶节点或终端节点:度为0的节点称为叶节点;
- 非终端节点或分支节点:度不为0的节点;
- 双亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点;
- 孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点;
- 兄弟节点:具有相同父节点的节点互称为兄弟节点;
- 树的度:一棵树中,最大的节点的度称为树的度;
- 节点的层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推;
- 树的高度或深度:树中节点的最大层次;
- 堂兄弟节点:双亲在同一层的节点互为堂兄弟;
- 节点的祖先:从根到该节点所经分支上的所有节点;
- 子孙:以某节点为根的子树中任一节点都称为该节点的子孙。
- 森林:由m(m>=0)棵互不相交的树的集合称为森林;
3 树模拟文件系统示例
class Node: def __init__(self, name, type='dir'): self.name = name self.type = type # "dir" or "file" self.children = [] self.parent = None def __repr__(self): return self.name class FileSystemTree: def __init__(self): self.root = Node("/") self.now = self.root # 当前目录 def mkdir(self, name): # name已/结尾的文件夹 if name[-1] != "/": name += "/" node = Node(name) self.now.children.append(node) node.parent = self.now def ls(self): return self.now.children def cd(self, name): if name[-1] != "/": name += "/" if name == "../": self.now = self.now.parent return for child in self.now.children: if child.name == name: self.now = child return raise ValueError("invalid dir") tree = FileSystemTree() tree.mkdir("var/") tree.mkdir("bin/") tree.mkdir("usr/") print(tree.root.children) print(tree.ls()) tree.cd('bin/') tree.mkdir('python/') print(tree.ls()) tree.cd("../") print(tree.ls())
二、二叉树
二叉树的链式存储:将二叉树的节点定义为一个对象,节点之间通过类似链表的链接方式来连接
* 度不超过2的树
* 每个节点最多有两个孩子节点
* 两个孩子节点被区分为左孩子节点和右孩子节点
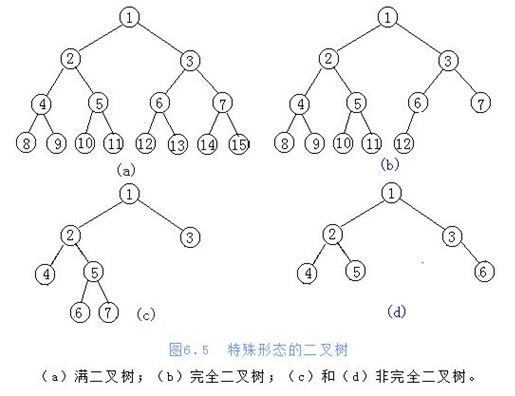
满二叉树:一个二叉树如果每一个层的节点数达到最大值,则这个二叉树就是满二叉树
完全二叉树:叶节点只能出现在最下层和次下层,并且最下面一层的节点都集中在该层最左边的若干位置的二叉树
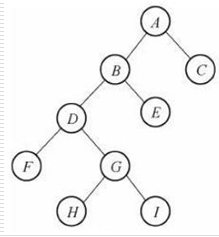
二叉树的遍历方式:
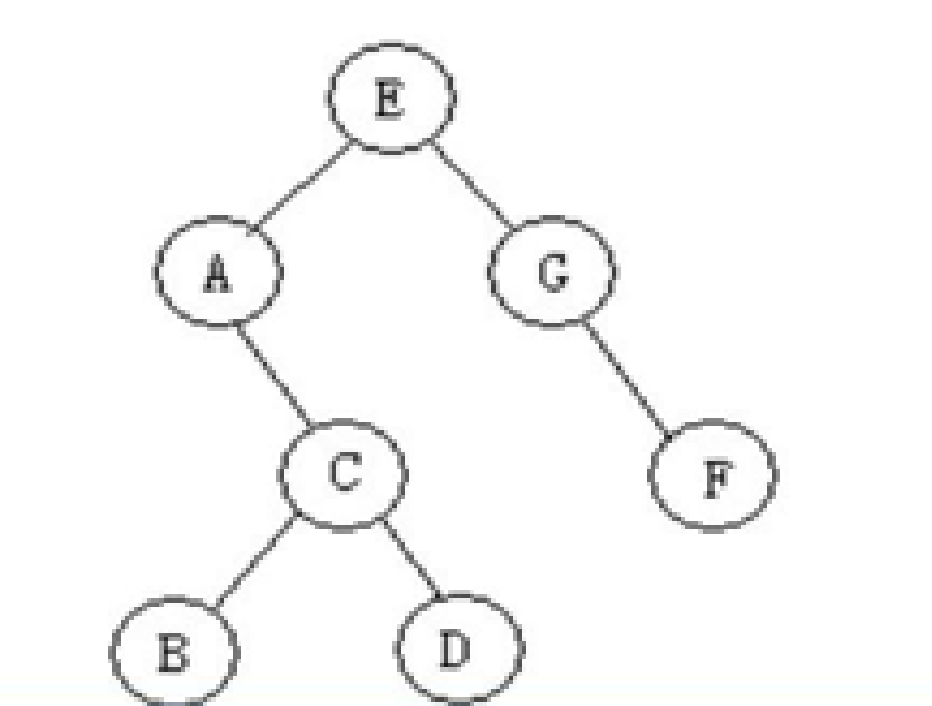
- 前序遍历: EACBDGF
- 中序遍历: ABCDEGF
- 后序遍历: BDCAFGE
- 层次遍历: EAGCFBD
from collections import deque class BiTreeNode: def __init__(self, data): self.data = data self.lchild = None self.rchild = None def level_order(root): queue = deque() queue.append(root) while len(queue) > 0: # 只要栈不空 node = queue.popleft() print(node.data, end=',') if node.lchild: queue.append(node.lchild) if node.rchild: queue.append(node.rchild) root = BiTreeNode(100) root.lchild = BiTreeNode(30) root.rchild = BiTreeNode(102) level_order(root)
三 二叉搜索树
二叉搜索树是一棵二叉树且满足性质:设X是二叉树的一个节点。如果y是x左子树的一个节点,那么y.key <= x.key;
如果y是x右子树的一个节点,那么y.key >= x.key。
二叉搜索树的操作:查询 插入 删除
1 删除操作
如果要删除的节点是叶子节点:直接删除
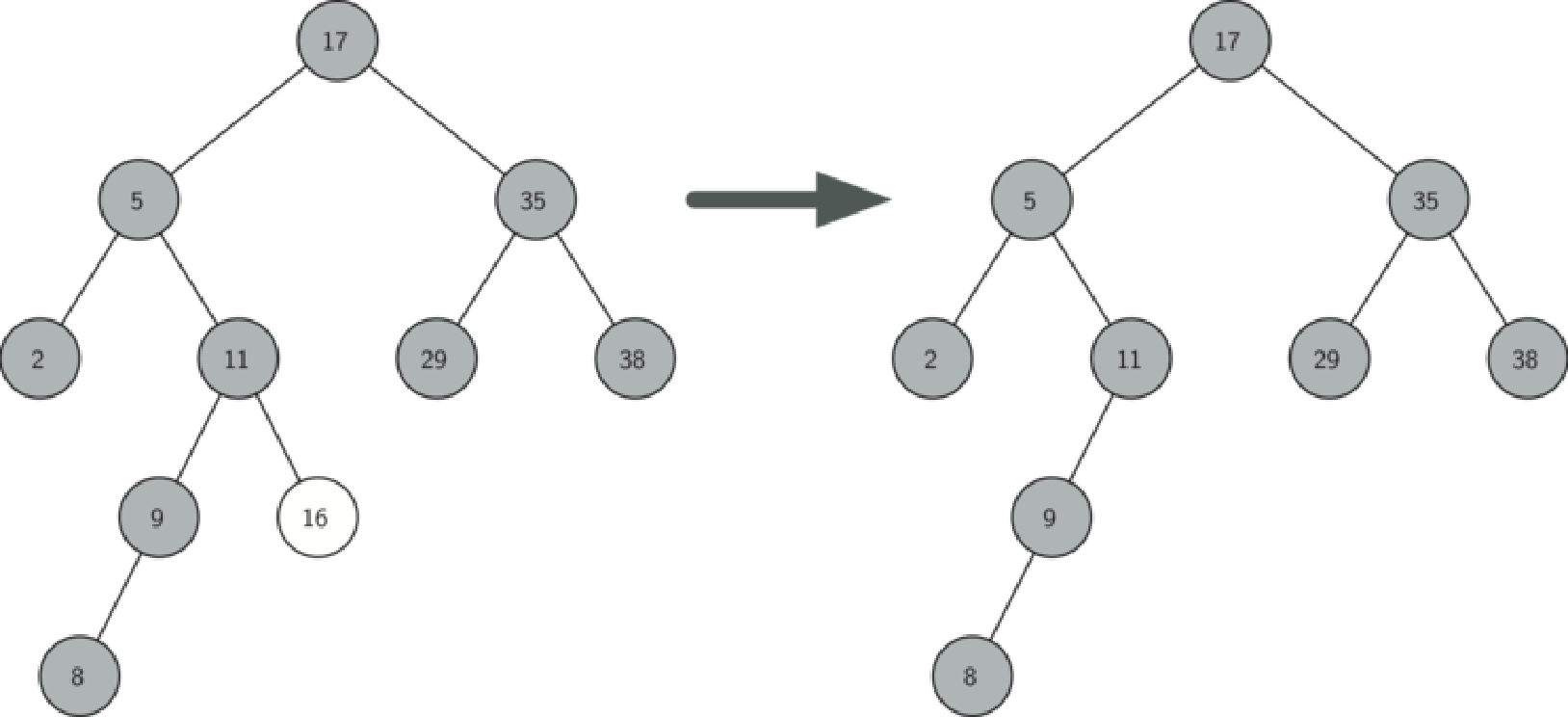
.如果要删除的节点只有一个孩子:将此节点的父亲与孩子连接,然后删除该节点
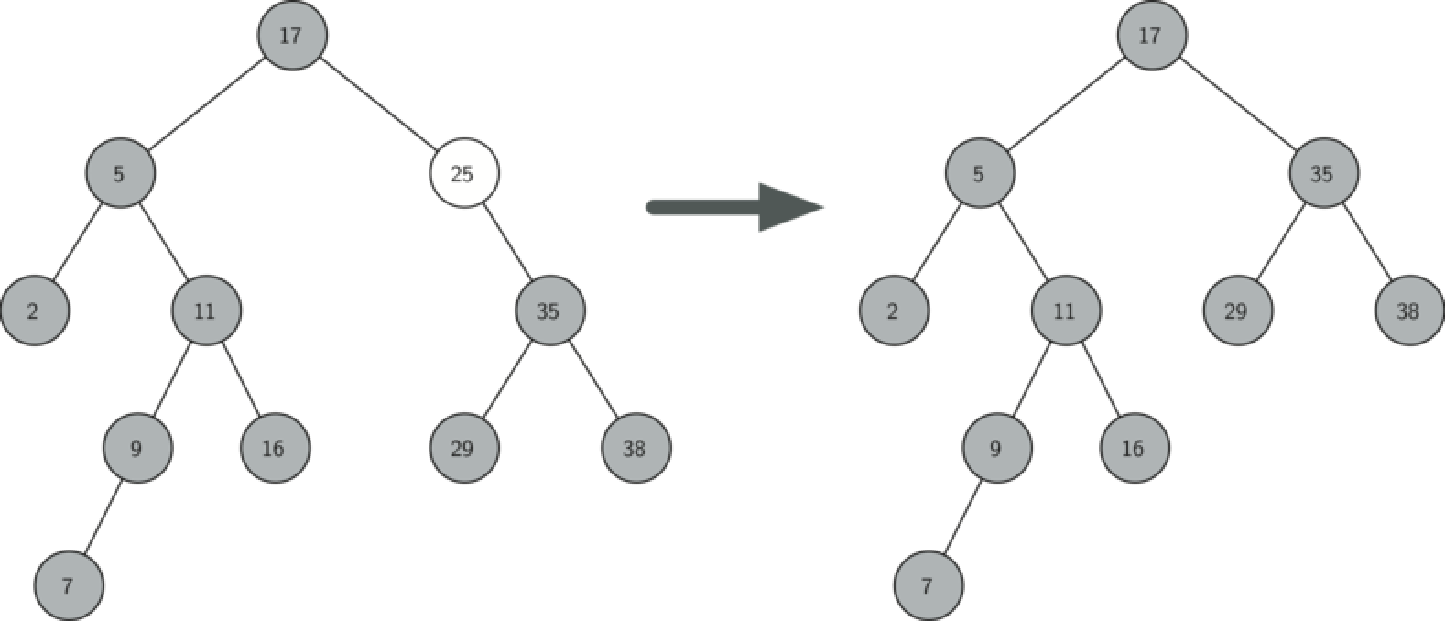
如果要删除的节点有两个孩子:将其右子树的最小节点(该节点最多有一个右孩子)删除,并替换当前节点。
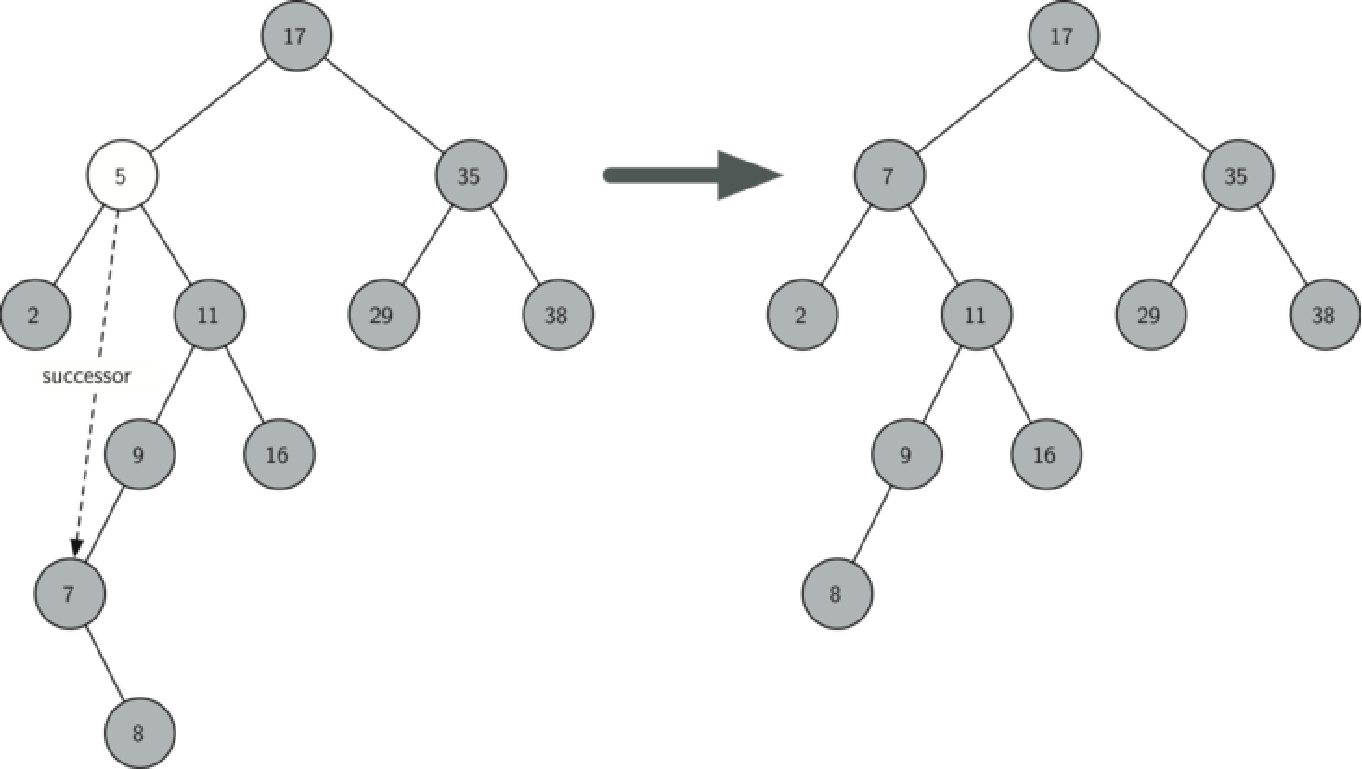
2 实现代码
class BiTreeNode: def __init__(self, data): self.data = data self.lchild = None self.rchild = None self.parent = None class BST: def __init__(self, li=None): self.root = None if li: for val in li: self.insert_no_rec(val) def insert(self, node, val): if not node: node = BiTreeNode(val) elif val < node.data: node.lchild = self.insert(node.lchild, val) node.lchild.parent = node elif val > node.data: node.rchild = self.insert(node.rchild, val) node.rchild.parent = node return node def insert_no_rec(self, val): ''' 非递归插入 :param val: :return: ''' p = self.root if not p: # 空树 self.root = BiTreeNode(val) return while True: if val < p.data: if p.lchild: p = p.lchild else: # 左子树不存在直接插入 p.lchild = BiTreeNode(val) p.lchild.parent = p elif val > p.data: if p.rchild: p = p.rchild else: p.rchild = BiTreeNode(val) p.rchild.parent = p else: return def query(self, node, val): if not node: return None if node.data < val: return self.query(node.rchild, val) elif node.data > val: return self.query(node.lchild, val) else: return node def query_no_rec(self, val): p = self.root while p: if p.data < val: p = p.rchild elif p.data > val: p = p.lchild else: return p return None def pre_order(self, root): if root: print(root.data, end=",") self.pre_order(root.lchild) self.pre_order(root.rchild) def in_order(self, root): if root: self.in_order(root.lchild) print(root.data, end=',') self.in_order(root.rchild) def post_order(self, root): if root: self.post_order(root.lchild) self.post_order(root.rchild) print(root.data, end=',') def __remove_node_1(self, node): # 情况1: node是叶子节点 if not node.parent: self.root = None if node == node.parent.lchild: # node是它父亲的左孩子 node.parent.lchild = None else: # 右孩子 node.parent.rchild = None def __remove_node_21(self, node): # 情况2: node只有一个左孩子 if not node.parent: # 根节点 self.root = node.lchild node.lchild.parent = None elif node == node.parent.lchild: node.parent.lchild = node.lchild node.lchild.parent = node.parent else: node.parent.rchild = node.lchild node.lchild.parent = node.parent def __remove_node_22(self, node): # 情况2.2: node只有一个右孩子 if not node.parent: self.root = node.rchild elif node == node.parent.lchild: node.parent.lchild = node.rchild node.rchild.parent = node.parent else: node.parent.rchild = node.rchild node.rchild.parent = node.parent def delete(self, val): if self.root: # 不是空树 node = self.query_no_rec(val) if not node: # 要删除的节点不存在 return False if not node.lchild and not node.rchild: self.__remove_node_1(node) elif not node.rchild: # 只有一个左孩子 self.__remove_node_21(node) elif not node.lchild: # 只有一个右孩子 self.__remove_node_22(node) else: # 两个孩子都有 min_mode = node.rchild # 找右子树最小的节点 while min_mode.lchild: min_mode = min_mode.lchild node.data = min_mode.data # 删除min_node if min_mode.rchild: self.__remove_node_22(min_mode) else: self.__remove_node_1(min_mode) import random li = list(range(0, 500, 2)) random.shuffle(li) tree = BST([1, 4, 2, 5, 3, 8, 6, 9, 7]) tree.in_order(tree.root) print("") tree.delete(4) tree.delete(1) tree.in_order(tree.root)
四 二叉搜索树效率
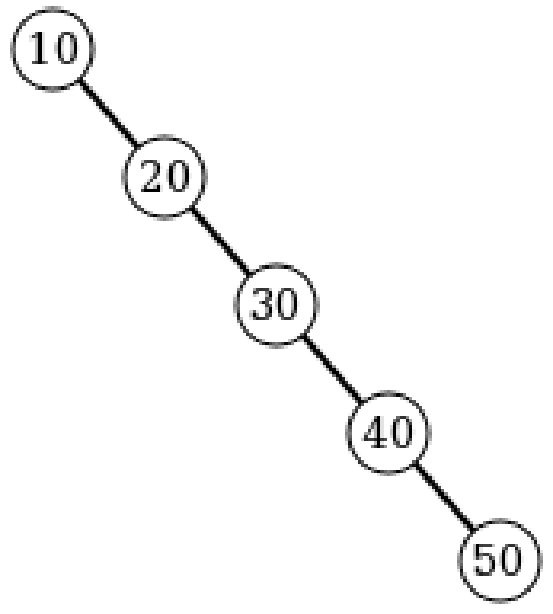
平均情况下,二叉搜索树进行搜索的时间复杂度为O(nlgn)。 最坏情况下,二叉搜索树可能非常偏斜。
解决方案:
- 随机化插入
- AVL树